ИССЛЕДОВАНИЕ  ВЕРОЯТНОСТНО-ВРЕМЕННЫХ  ХАРАКТЕРИСТИК  МНОГОПРОЦЕССОРНОЙ  СИСТЕМЫ  С  ДИСПЕТЧЕРОМ  ЗАДАЧ  СО  СТРАТЕГИЕЙ  РАЗДЕЛЕНИЯ  ВО  ВРЕМЕНИ

Мартышкин  Алексей  Иванович

канд.  техн.  наук,  доцент  кафедры  Вычислительных  машин  и  систем  Пензенского  государственного  технологического  университета,  РФ,  г.  Пенза

E-mail: 

INVESTIGATION  OF  PROBABILISTIC   AND  TEMPORAL  CHARACTERISTICS  OF  MULTIPROCESSOR  SYSTEM  WITH  TASK  MANAGER  WITH  STRATEGIES  OF  SEPARATION  IN  TIME

Alexey  Martyshkin

candidate  of  Science,  assistant  professor  Department   of  Computational  Systems  and  Machines  of  Penza  State  Technological  University,  Russia,  Penza

Работа  выполнена  при  финансовой  поддержке  стипендии  Президента  РФ  на  2012—2014  гг.  (СП-1172.2012.5).

АННОТАЦИЯ

В  статье  приводятся  полученные  в  ходе  вычислительного  эксперимента  по  моделированию  диспетчеров  задач  со  стратегией  разделения  во  времени  для  многопроцессорных  систем  на  основе  разомкнутых  сетей  массового  обслуживания  результаты.  Проведено  моделирование  и  исследованы  результаты,  полученные  при  классическом,  имитационном  моделировании  и  при  разработанном  автором  методе  моделирования.  В  заключении  статьи  сделаны  соответствующие  выводы.

ABSTRACT

The  article  provides  results  obtained  in  the  course  computational  experiment  on  modeling  Task  Managers  with  the  strategy  of  separation  in  time  for  multiprocessor  systems  based  on  open  Queueing  Networks.  The  simulation  and  investigated  the  results  obtained  with  classical  simulation  modeling  and  simulation  method  developed  by  the  author.  The  article  concludes  by  corresponding  conclusions.

Ключевые  слова:  математическая  модель;  диспетчер  задач;  разделение  во  времени;  стохастическая  сеть;  вероятность

Keywords:   mathematical  model;  task  manager;  separation  in  time;  stochastic  network;  probability

При  исследовании  вычислительных  систем  (ВС)  адекватно  отражает  процесс  их  функционирования  аппарат  теории  массового  обслуживания.  Зачастую  для  упрощения  модели  реальной  системы  опускают  ряд  факторов.  В  существующем  методе  моделирования  (в  методе  моделирования  диспетчеров  задач  (ДЗ)  со  стратегией  разделения  во  времени  многопроцессорных  систем  (МПС))  имеют  место  следующие  недостатки:  1)  неограниченная  длина  очереди,  что  противоречит  принципу  ограниченности  ресурсов  ВС;  2)  отсутствует  модель  конфликтов  за  общую  очередь  задач  со  стороны  множества  центральных  процессоров  (ЦП);  3)  не  учитываются  задержки,  связанные  с  переключением  контекста  задачи  и  перезагрузкой  кэш-памяти  ЦП.

Обозначим  существующий  метод  как  базовый,  под  которым  понимается  метод  моделирования  СеМО,  основанный  на  СМО  с  простейшими  потоками  задач,  экспоненциальным  временем  обслуживания,  неограниченной  очередью  заявок  и  бесприоритетной  дисциплиной  обслуживания.  Рассмотрим  базовый  метод  моделирования,  чтобы  определить  относительно  него  адекватность  разработанного  в  [1]  метода.  Характеристики  базовой  и  исследуемой  системы  одинаковы,  отличием  является  общая  очередь  перед  блоком  ЦП  (в  базовом  (классическом)  варианте  она  принята  неограниченной  длины),  также  отличительной  особенностью  является  наличие  ДЗ  для  устранения  конфликтов  за  доступ  к  общей  очереди  задач  перед  блоком  ЦП.  Для  проведения  вычислительного  эксперимента  приняты  следующие  параметры  МПС:  число  ЦП  от  2  до  20;  интенсивность  входящего  потока  задач    для  задач  с  высокой  реакцией  изменялась  от  6,5  до  65  задач/мс,  для  задач  со  средней  реакцией  изменялась  от  0,416  до  4,16  задач/мс,  для  задач  со  средней  реакцией  изменялась  от  0,13  до  1,3  задач/мс.  Такие  значения  интенсивностей  обеспечивают  среднюю  загрузку  ЦП  на  уровне  65  %  (ρ_ЦП=0,65);  длина  общей  очереди  в  базовой  системы  принята  неограниченного  размера,  в  системе  с  ДЗ  длина  общей  очереди  принята  равной  128  задач;  среднее  время  работы  ДЗ,  учитывая  время  перезагрузки  кэш-памяти  и  переключения  контекста  задач,  составляет  0,015  мс.

Известно,  что  в  системах  реального  времени  (СРВ)  имеется  потенциал  производительности  ЦП,  чтобы  можно  было  решать  «короткие»  задачи  [2].  При  моделировании  учитывалась  трудоемкость  задач:  низкая  или  высокая,  а  также  реакция  на  запрос.  Трудоемкость  варьировалась  путем  изменения  времени  обслуживания  в  ЦП.

Теперь  рассмотрим  систему  с  ограниченной  общей  очередью  и  ограничением  числа  источников  запросов  ДЗ.  На  рис.  1  представлен  граф  такой  системы.

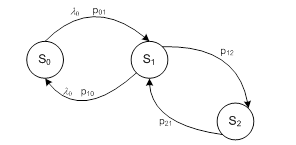
Рисунок  1.  Граф  передач  системы  с  общим  ДЗ  со  стратегией  разделения  во  времени

На  рис.  1:    —  предварительный  планировщик  —  источник  запросов,    —  ЦП,  —  ДЗ.

Распишем  выражение,  полученное  в  [1]  более  подробно

,                                         (1)

где:    —  время  ожидания  в  очереди  перед  ЦП; 

  —  время  ожидании  ЦП  перед  занятием  ДЗ; 

  —  вероятность  выхода  обработанной  задачи  из  системы;

  —  вероятность  перехода  задачи  на  обслуживание  в  ДЗ. 

Время  ответа  в  системе  с  ДЗ  и  общей  очередью  задач  в  МПС 

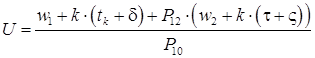,                      (2)

где:    —  число  квантов  на  выполнение  одной  задачи; 

  —  длительность  одного  кванта; 

  —  время,  необходимое  для  перезагрузки  кэш; 

  —  время  работы  ДЗ, 

  —  время,  необходимое  для  переключения  контекста  (ПК). 

Вероятности    и    зависят  от  трудоемкости  пришедшей  на  выполнение  задачи.  При  моделировании  прохождения  через  систему  трудоемких  задач  значения    и    задавались  0,1  и  0,9  соответственно.  При  рассмотрении  задач  средней  трудоемкости  значения  принимались  равными  0,16  и  0,84  соответственно.  При  моделировании  поступления  и  обслуживания  коротких,    и    принимались  равными  0,5  и  0,5  соответственно.  Все  расчеты  проводились  в  разработанной  программе  расчета  сетей  массового  обслуживания  (СеМО)  [3].

Были  получены  времена  ожидания  в  очередях  МПС  с  общим  ДЗ  с  разделением  во  времени,  времена  ответа  МПС  с  общим  ДЗ,  а  также  загрузка  ДЗ  от  трудоемкости  задач.  Результаты  представлены  в  виде  графиков  на  рис.  3  и  рис.  4.

Имитационное  моделирование.   Модель  описывает  процесс  обработки  задач  в  МПС.  Время  обработки  каждой  задачи  выбирается  при  генерировании  экспоненциально  по  значению  интенсивности  входного  потока  .  Среднее  время  обработки  задачи  выбирается  экспоненциально  по  произведению  времени  одного  кванта  ()  на  количество  квантов  (),  необходимых  для  полного  выполнения  задачи  ЦП.

Моделируемая  система  представляет  собой  массив  ЦП  с  общим  ДЗ  и  общей  очередью  задач  на  обслуживание.  Схема  имитационной  модели  представлена  на  рис.  2.

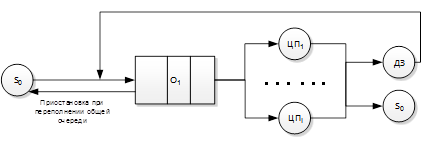
Рисунок  2.  Схема  МПС  с  общим  ДЗ.  Имитационное  моделирование

На  рис.  2:    —  источник  задач  (предварительный  планировщик);  O₁  —  очередь  задач,  ожидающих  обслуживания;  ДЗ,  ЦП₁-ЦП_i  —  диспетчер  задач  и  центральные  процессоры  соответственно.

Задачи  из  предварительного  планировщика  помещаются  в  очередь,  если  в  ней  имеются  свободные  места.  Иначе  они  покидают  вычислительную  систему  не  обработанными.  Из  очереди  задачи  равновероятно  назначаются  по  ЦП,  выбираясь  в  порядке  поступления  (FIFO),  они  выходят  из  очереди  и  поступают  на  обработку  в  соответствующий  i-й  ЦП.  Также  с  некоторой  вероятностью  перед  обработкой  очередной  поступившей  задачи  i-й  ЦП  перезагружает  кэш-память  (вероятность  перезагрузки  кэш-памяти  будет  равна  n-1/n  ,  где    —  число  ЦП  в  системе).

Задача  обрабатывается  на  i-м  ЦП  целый  квант  времени  ().  По  окончании  обработки  в  ЦП  из  внутренней  переменной  задачи  вычитается  время  обработки  —  время  одного  кванта  ().  Затем  происходит  проверка  на  завершенность  путем  сравнения  внутренней  переменной  задачи,  отвечающей  за  остаток  времени  необходимого  для  завершения  обработки,  с  нулем.  Если  задача  обработана  полностью,  то  она  покидает  систему.  Иначе  задача  ожидает  освобождения  ДЗ,  не  освобождая  до  тех  пор  i-й  ЦП,  создается  очередь  ожидающих  ЦП.  Как  только  ДЗ  освободится,  задача  переходит  на  обработку  в  него,  где  также  происходит  смена  ЦП.  Далее  задача  пытается  вернуться  в  общую  очередь  при  наличии  в  ней  свободного  места,  иначе  —  покидает  систему  частично  обработанной.

В  ходе  эксперимента  изменялась  трудоемкость  задач,  поступающих  на  выполнение  в  МПС.  Времена  следующие:  для  задач  с  низкой  трудоемкостью  —  0,1  мс,  со  средней  трудоемкостью  —  0,5  мс,  для  самых  трудоемких  —  1,0  мс.  Время  кванта  для  проведенных  опытов  принято  постоянным  и  равным  0,1  мс.  Время  работы  ДЗ  при  переключении  контекста  задач  составляет  5  мкс  (получено  измерением  на  системе-прототипе  с  помощью  программы  измерения  [4]);  время  перезагрузки  кэш-памяти  принято  равным  5  мкс  (оценка  получена  с  помощью  пакета  RightMark  Memory  Analyzer). 

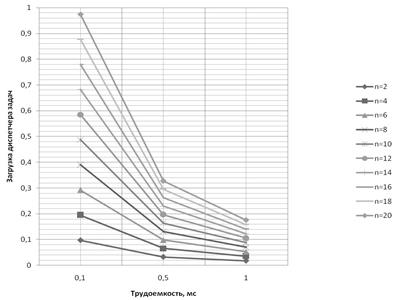
Рисунок  3.  Зависимость  загрузки  ДЗ  от  трудоемкости  задач  в  МПС  с  общим  ДЗ

Из  графика  (рис.  3)  следует,  что  загрузка  ДЗ  со  стратегией  разделения  во  времени  растет  с  понижением  трудоемкости  задач,  т.  е.  с  увеличением  реактивности  МПС. 

Зависимость  времени  ответа  МПС  от  числа  ЦП,  полученная  в  ходе  исследования  системы,  представлена  на  рис.  4.

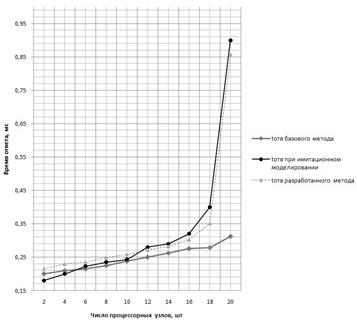
Рисунок  4.  Зависимость  времени  ответа  многопроцессорной  системы  от  числа  процессоров  при  потоке  задач,  требующих  высокой  реакции

Анализ  полученного  графика  показывает,  что  при  увеличении  числа  ЦП  резко  возрастет  время  ответа  в  модели,  использующей  разработанный  метод  и  метод  имитационного  моделирования,  что  говорит  об  адекватности  разработанного  метода.  Резкий  рост  времени  ответа  объясняется  высокой  загрузкой  ДЗ,  обслуживающего  множество  ЦП.  Модель,  использующая  базовый  метод,  ведет  себя  неадекватно  относительно  имитационного  метода  при  числе  процессоров  более  16  для  заданных  параметрах  задач  и  архитектурных  параметрах  МПС.  Это  свидетельствует  о  том,  что  точность  моделирования  базовым  методом  масштабных  МПС  резко  снижается.

В  результате  проведенных  экспериментов  выявлено,  что  число  ЦП  в  составе  МПС  зависит  от  параметров  задач  и  архитектурных  параметров  ДЗ.  Проведена  верификация  метода  математического  моделирования  для  оценки  показателей  производительности  ДЗ  с  разделением  во  времени  в  МПС  посредством  корреляционного  анализа.  Показано,  что  линейный  коэффициент  корреляции  существующего  метода  моделирования  с  имитационной  моделью  составляет  0,83,  а  разработанного  метода  приближается  к  единице  —  0,99.  Это  свидетельствует  о  большей  адекватности  разработанного  метода  моделирования  процессам  в  реальной  системе,  чем  при  использовании  традиционных  методов,  основанных  на  экспоненциальных  разомкнутых  СеМО.

Список  литературы:

1.Мартышкин  А.И.  Математическое  моделирование  диспетчеров  задач  для  систем  параллельной  обработки  на  основе  разомкнутых  систем  массового  обслуживания  /  А.И.  Мартышкин,  Р.А.  Бикташев,  Н.Г.  Востоков  //  В  мире  научных  открытий.  —  2013.  —  №  6.1  (42)  (Математика.  Механика.  Информатика).  —  С.  81—101.

2.Таненбаум  Э.  Современные  операционные  системы  /  Э.  Таненбаум.  2-е  изд.  СПб.:  Питер,  2002.  —  1040  с.

3.Свидетельство  о  государственной  регистрации  программы  для  ЭВМ  №  2013611117. 

4.Свидетельство  о  государственной  регистрации  программы  для  ЭВМ  №  2013611118.