ИССЛЕДОВАНИЕ  УСТОЙЧИВОСТИ  СТРУКТУР  В  СМЕКТИЧЕСКИХ  ЖИДКИХ  КРИСТАЛЛАХ  В  ЭЛЕКТРИЧЕСКОМ  ПОЛЕ

Мигранова  Дана  Наилевна

старший  преподаватель  БКИ  РУК,  РФ,  г.  Уфа

E -mail:  danakiprida@ya.ru

Кондратьев  Денис  Васильевич

канд.  физ.-мат.  наук,  ученый  секретарь  АН  РБ,  РФ,  г.  Уфа

E-mail: 

Мигранов  Наиль  Галиханович

д-р  физ.-мат.  наук,  профессор  БГПУ,  РФ,  г.  Уфа

E-mail: 

STABILITY  OF  STRUCTURES  IN  SMECTIC  LIQUID  CRYSTALS  IN  ELECTRIC  FIELD

Migranova  Dana

senior  lecturer  of  Bashkir  Cooperative  Institute  of  the  Russian  University  of  Cooperation,  Russia,  Ufa

Kondratyev  Denis

candidate  of  Sciences,  Academic  secretary,  Academy  of  Sciences  of  the  Republic  of  Bashkortostan,  Russia,  Ufa

Migranov  Nail

doctor  of  Sciences,  Professor  of  Bashkir  State  Pedagogical  University,  Russia,  Ufa

Работа  выполнена  при  поддержке  Академии  наук  Республики  Башкортостан  и  Российского  Фонда  Фундаментальных  Исследований  в  рамках  проекта  14-02-97026. 

АННОТАЦИЯ

Рассмотрено  решение  задачи  структурообразования  в  тонком  слое  смектического  жидкого  кристалла  со  спонтанной  поляризацией  «bookshelf»  под  действием  приложенного  под  разными  углами  электрического  поля.  Рассмотрена  двумерная  задача  с  периодическими  граничными  условиями  вызывающими  эффект  соизмеримости/несоизмеримости  вдоль  слоев  SmC*.

ABSTRACT

Solution  of  the  problem  of  structure  formation  in  a  thin  layer  of  a  ferroelectric  liquid  crystals  with  geometry  «bookshelf»  under  applied  at  different  angles  of  the  electric  field  is  theoretically  investigated.  The  two-dimensional  problem  with  periodic  boundary  conditions,  the  effect  of  commensurability  /  incommensurability  along  the  fibers  of  SmC  *  are  under  consideration  as  well.

Ключевые  слова:  смектик;  спонтанная  поляризация;  соизмеримые  структуры;  несоизмеримые  структуры;  сегнетоэлектрик.

Keywords:  smectic;  spontaneous  polarization;  commensurate  structures;  incommensurate  structures;  ferroelectric.

Рассмотрим  сегнетоэлектрический  жидкий  кристалл  (ЖК)  подобные  смектики  имеют  закрученные  от  слоя  к  слою  молекулы,  которые  описываются  единичным  вектором  .  В  обычном  смектике  C  директор  в  каждом  слое  наклонен  к  нормали    под  углом    (Рис.  1).

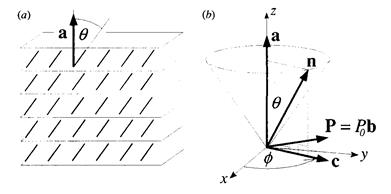
Рисунок  1.

В  общем  случае  угол    зависит  от  температуры:  с  понижением  температуры  он  становится  меньше.  Запишем  директор    в  виде

,

где:    —  нормаль  к  слою, 

  —  единичный  вектор  характеризующий  направление  проекции  директора    в  слое.

В  рассматриваемом  SmC*  присутствует  спонтанная  поляризация  ,  которая  всегда  перпендикулярна  плоскости  .  Удобно  ввести  вектор    для  описания  .  Рассмотрим  положительную  поляризацию  .  Известно,  что  внешние  электрические  поля  переориентируют  директор  в  слоях  из-за  наличия  дипольных  моментов  молекул.

Целью  данной  работы  является  получение  равновесного  решения  для  образца  SmC*  в  геометрии  “bookshelf”,  когда  не  учитывается  геликоидальная  структура  исследуемого  материала.  В  достаточно  тонких  слоях  граничные  условия  подавляют  эту  тенденцию.

Электрическое  поле  прикладывается  под  углом    к  оси  Ox 

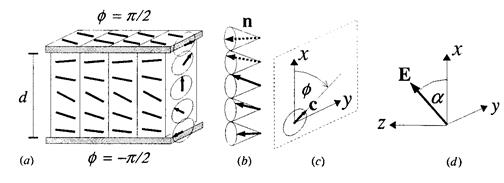
Рисунок  2.

Предполагаем  отсутствие  конвективных  потоков  при  воздействии  внешним  полем,  прикладываемые  поля  меньше  критических  значений.

Нормали    и  ,  введенные  ранее,  удовлетворяют  следующим  условиям:

,  ,  .

Известно,  что  энергия  упругости  сегнетоэлектрического  ЖК  в  декартовой  системе  координат  [3,  c.  310].

(1)

где  на  константы  упругости  накладываются  ограничения  [4,  с.  1855]

,  ,  ,,  ,  ,

,  ,  .

Константы    связаны  с  изгибами  смектических  слоев,    соответствуют  возмущению  вектора  ,    —  это  константы,  соответствующие  разным  слоевым  деформациям,  описываемых  искажением  вектора  .

Электрический  вклад  в  энергию  [4,  с.  1856]

,  (2)

где    электрическое  поле,  Ф/м,    —  диэлектрическая  анизотропия.  При    директор  ориентируется  параллельно  направлению  поля,  при    —  перпендикулярно  (в  данном  случае,    отрицательная  величина).  В  первом  слагаемом  в  (2)  принимает  минимальное  значение  при  .

Плотность  энергии  для  смектика  C*

.  (3)

Тогда  полная  энергия

,

где:    —  объем  образца.

В  отсутствие  потоков  динамические  уравнения,  описывающие  смектик  C*  во  внешнем  электрическом  поле,  разбиваются  на  систему  уравнений  для    и  .

В  рассматриваемой  модели  смектические  слои  остаются  невозмущенными,  поэтому  нормаль    будет  константой.  Уравнение  для    имеет  следующий  вид  [3,  с.  313]

,  ,  (4)

где

,

.

Параметр    —  положительный  коэффициент  вязкости  связанный  с  вращением  директора  в  смектическом  слое  по  образующей  конуса  (рис.  1).

Скалярные  функции    и    —  множители  Лагранжа,  которые  могут  быть  найдены  из  скалярного  произведения  уравнения  (4)  с  векторами    и  .

Рассмотрим  образец  сегнетоэлектрического  ЖК  SmC*  в  геометрии  “bookshelf”  (рис.  2).  Электрическое  поле    приложено  под  углом    к  плоскости  смектических  слоев.  Вектор    описывается  азимутальным  углом,  показанным  на  рис.  2с.

Распределение  директора  по  верхней  и  нижней  границам  предполагается  периодическим  вдоль  оси  Oy  —  соответствующие  граничные  условия  приведены  ниже.

В  соответствии  с  предложенной  геометрией  нашей  задачи  можно  записать:  ,  ,  ,  ,  .

По  аналогии  с  [3,  с.  314]  в  одноконстантном  приближении  при    получим  динамическое  уравнение  для    в  виде

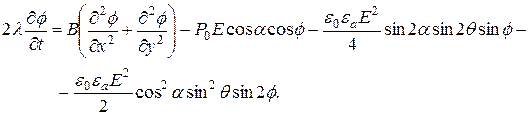  (5)

В  стационарном  случае  (5)  переходит  в

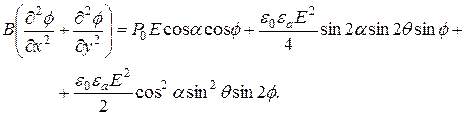  (6)

В  нашей  постановке  задачи  граничные  условия  имеют  следующий  вид:

,  (7)

,  (8)

где  функция  Хевисайда  доопределена  в  0,  а  именно  .

Займемся  решением  уравнения  (6)  с  учетом  граничных  условий  (7),  (8)  и  исследованием  устойчивости  решений.  Задача  для  образца  нематического  жидкого  кристалла  с  подобными  периодическими  граничными  условиями  решалась  в  [1,  с.  42],  случай  полосчатых  граничных  условий  рассмотрен  в  [2,  с.  93].

Расчеты  выполнены  для  значений  параметров:    Ф/м,  ,  ,  ,  ,  м,  ,  ,    м^-1.  График  зависимости    при    приведен  на  рис.  3.

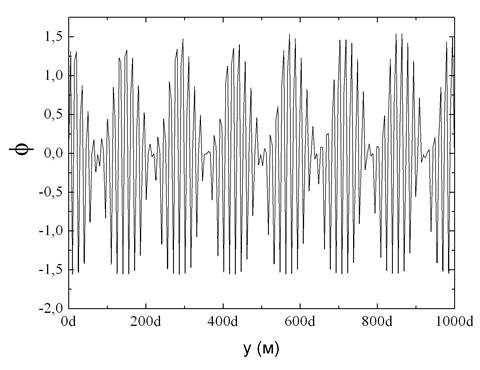
Рисунок  3.

Особенность  нашей  задачи  состоит  в  том,  что  в  предложенной  модели  появляются  искажения  поля  директора,  зависящие  от  переменной  .  Варьируя  длину  периода  на  верхней  и  нижней  пластинах  мы  получаем  пространственные  структуры  сегнетоэлектрического  ЖК.

При  наложении  влияния  граничных  условий  внутри  объема  сегнетоэлектрика  появляются  периодические  макроструктуры,  которые  занимают  центральные  слои  образца  смектика.

Список  литературы:

1.Кондратьев  Д.В.,  Мигранов  Н.Г.  Построение  функционала,  описывающего  макроструктуры  в  тонком  слое  нематического  жидкого  кристалла  //  Вестник  ЧелГУ.  —  2010.  —  №  12.  —  С.  41—46.

2.Кондратьев  Д.В.,  Мигранов  Н.Г.  Распределение  молекул  нематического  жидкого  кристалла  в  полупространстве,  ограниченном  структурированной  подложкой  //  Вестн.  Помор.  ун-та.  Сер:  Естествен.  науки.  —  2009.  —  №  3.  —  С.  91—95.

3.Stewart  I.W.  The  static  and  dynamic  continuum  theory  of  liquid  crystals.  London  and  New  York:  Taylor  and  Francis,  2004.  —  360  с.

4.Stewart  I.W.  Stability  of  equilibrium  states  in  finite  samples  of  smectic  C*  liquid  crystals  //  J.  Phys.  A:  Math.  Gen.  —  2005.  —  Vol.  38.  —  P.  1853—1873.