ИЗМЕНЕНИЕ  ОБЛАСТИ  УСТОЙЧИВОСТИ  КОЛЬЦЕВОЙ  НЕЙРОННОЙ  СЕТИ  ПРИ  ДОБАВЛЕНИИ  СВЯЗЕЙ  МЕЖДУ  НЕЙРОНАМИ

Кипнис  Михаил  Маркович

д-р  физ.-мат.  наук,  профессор,  кафедра  математики  и  методики  обучения  математике.  Челябинский  государственный  педагогический  университет  (ЧГПУ),  РФ,  г.  Челябинск

Божков  Евгений  Владимирович

магистрант  ЧГПУ,  РФ,  г.  Челябинск

Важенина  Ирина  Витальевна

магистрант  ЧГПУ,  РФ,  г.  Челябинск

Королев  Владимир  Александрович

магистрант  ЧГПУ,  РФ,  г.  Челябинск

E-mail: 

CHANGING  OF  THE  STABILITY  DOMAIN  OF  A  RING  NEURAL  NETWORK  WITH  THE  ADDITION  OF  CONNECTIONS  BETWEEN  NEURONS

Kipnis  Mikhail

professor,  PhD,  Department  of  Mathematics,  Chelyabinsk  State  Pedagogical  University  (CSPU),  Russia,  Chelyabinsk

Bozhkov  Evgeniy

graduate  student,  Dept.  of  Computer  Science   (CSPU),  Russia,  Chelyabinsk

Vazhenina  Irina

graduate  student,  Dept.  of  Computer  Science  (CSPU),  Russia,  Chelyabinsk

Korolev  Vladimir

graduate  student,  Dept.  of  Computer  Science  (CSPU),  Russia,  Chelyabinsk

АННОТАЦИЯ

Мы  рассматриваем  изменение  области  устойчивости  дискретной  модели  кольцевой  нейронной  сети  сначала  при  добавлении  к  ней  двух  связей,  затем  при  переходе  к  полной  системе  связей.  Численными  экспериментами  установлено,  что,  за  некоторым  исключением,  добавление  связей  уменьшает  область  устойчивости  в  пространстве  параметров. 

ABSTRACT

We  consider  changes  in  the  stability  domains  of  discrete  ring  neural  network  model  with  the  addition  firstly  one  or  two  connections  and,  finally,  full  system  of  the  network  connections.  By  means  of  numerical  experiments  we  found  that  (with  some  exceptions)  the  stability  domain  of  the  parameter  space  of  the  tested  network  shrinks  when  we  add  the  connections  to  the  network. 

Ключевые  слова :  нейронные  сети;  дискретная  модель;  устойчивость;  кольцевая  конфигурация.

Keywords :  neural  networks;  discrete-time  model;  stability,  ring.

Области  устойчивости  в  пространстве  параметров  нейронных  сетей  изучались,  например  в  [1,  2,  4,  5].  В  [5]  было  показано,  что  при  разрыве  кольцевой  нейронной  сети  область  устойчивости  в  пространстве  параметров,  вообще  говоря,  расширяется.  Но  это  исследование  можно  рассматривать  и  в  обратном  порядке:  при  добавлении  перемычки  между  первым  и  последним  нейронами  сети  область  устойчивости  в  пространстве  параметров  сжимается.

Возникает  естественный  вопрос:  что  происходит  с  областями  устойчивости  при  дальнейшем  добавлении  перемычек  в  кольцевую  сеть,  вплоть  до  превращения  ее  в  полносвязную  нейронную  сеть.

Эта  задача  и  решена  в  данной  заметке  для  частного  случая  шести-нейронной  кольцевой  сети.  Мы  выяснили,  что  в  данном  процессе  происходит  дальнейшее  сужение  области  устойчивости  в  пространстве  параметров  нейронной  сети,  но,  как  и  в  работах  [2,  5],  в  наших  численных  экспериментах  обнаружены  так  называемые  парадоксальные  точки  в  пространстве  параметров,  в  которых  система  приобретает  устойчивость  при  добавлении  дополнительных  перемычек.

Исследуемая  сеть  состоит  из  шести  нейронов  (Рис.  1). 

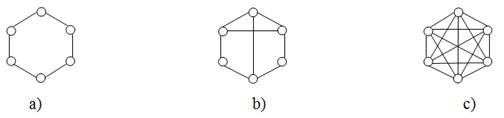
Рисунок  1.  Конфигурации  нейронных  сетей:  a )  кольцевая;  b)  кольцевая  с  двумя  перемычками;  c)  полносвязная  сеть

В  одной  из  работ  (см.  [6])  кольцевая  нейронная  сеть  с  добавлением  одной-двух  связей  рассматривается  как  модель  «small  world  networks»,  связанная  с  известной  гипотезой  о  шести  рукопожатиях. 

Кольцевая  сеть  (Рис.  1а)  описывается  линейной  системой  разностных  уравнений  шестого  порядка

                    (1)

Здесь    шестимерный  вектор  состояния  сети  в  момент  времени  ,    коэффициент  демпфирования  ,    запаздывание  во  взаимодействии  различных  нейронов,    матрица  взаимодействий  различных  нейронов.

Для  кольцевой  сети  (Рис.  1а) 

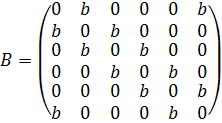,             (2)

где    сила  взаимодействия  между  соседними  нейронами  в  кольце. 

Система  (1)  называется  устойчивой,  если  при  любых  начальных  условиях  для  любого  ее  решения    имеет  место    при  .  Характеристическое  уравнение  [2]  для  (1)  имеет  вид

      (3)

где    единичная  матрица.  Если  все  корни    ()  удовлетворяют  усло-вию  ,  то  система  устойчива,  если  при  некотором  ,  то  система  неустойчива.

Мы  фиксируем  запаздывание  .  Мы  ставим  задачу  вначале  построить  область  устойчивости  в  плоскости    для  кольцевой  сети  (Рис.  1а),  описанной  уравнением  (1)  с  матрицей  ,  указанной  в  (2).  Затем  мы  находим  область  устойчивости  кольцевой  сети  с  двумя  перемычками  (Рис.  1b),  описанной  тем  же  уравнением  (1),  в  котором  матрица    заменена  матрицей  :

.

Наконец,  последняя  исследуемая  модель  является  полносвязной  сетью  (Рис.  1c)  с  заменой  в  уравнении  (1)  матрицы    на  матрицу 

  .

Методы  исследования  —  численные  эксперименты  в  Mathcad.  Некоторые  подробности  техники  проведения  численных  экспериментов  указаны  в  [1]. 

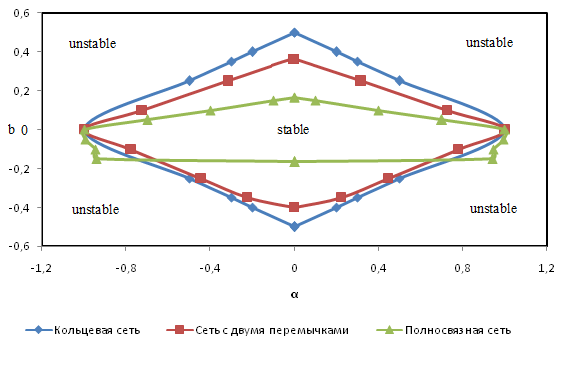
Рисунок  2.  Границы  областей  устойчивости  нейронных  сетей,  изображенных  на  Рисунке  1

Результаты  поиска  границ  области  устойчивости  показаны  на  Рис.  2. 

Как  показывает  Рис.  2,  области  устойчивости  в  пространстве  параметров  ,  в  общем,  сужаются  при  добавлении  перемычек.  Однако,  существуют  небольшие  области  параметров  (по  аналогии  с  [5]  их  можно  назвать  парадоксальными),  при  которых  добавление  перемычек  переводит  систему  из  класса  неустойчивых  в  класс  устойчивых. 

Три  графа  на  Рис.  1  имеют  диаметры  3,  2,  1  соответственно  (определение  диаметра  графа  см.  в  [3]).  Из  трех  изученных  нами  нейронных  сетей  примечательна  сеть,  представленная  на  Рис.  1b  .  Ее  можно  назвать  сетью  “small  world”  [6],  то  есть  сетью  с  небольшим  количеством  связей,  в  которой  переход  от  нейрона  к  любому  другому  нейрону  происходит  через  небольшое  количество  посредников.  Настоящая  работа  показывает,  что  система  «small  world»,  вообще  говоря,  менее  устойчива,  чем  кольцевая  сеть.

Список   литературы:

1.Иванов  С.А.,  Невзорова  Е.Н.,  Козлова  С.А.  Устойчивость  рекурсивных  нейронных  сетей  цилиндрической  архитектуры  с  запаздывающими  взаимодействиями.  «Инновации  в  науке»:  материалы  XVI  международной  заочной  научно-практической  конференции.  Часть  I.  (28.01.2013  г.).  Новосибирск:  «СибАК»,  2013,  —  с.  7—11.

2.Речкалова  Л.В.,  Кипнис  М.М.  Область  устойчивости  нейронной  сети  с  топологией  в  виде  тора  при  разрыве  некоторых  связей.  «Инновации  в  науке»:  сборник  статей  по  материалам  XXVIII  международной  научно-практической  конференции  №  12(25).  Новосибирск:  «СибАК»,  2013,  —  c.  23—31.

3.Уилсон  Р.  Введение  в  теорию  графов.  М.:  Мир,  1977,  —  208  стр.

4.Ivanov  S.A.,  Kipnis  M.M.  Stability  analysis  of  discrete-time  neural  networks  with  delayed  interactions:  torus,  ring,  grid,  line.  International  Journal  of  Pure  and  Applied  Math.  (2012)  V.  78(5),  —  p.  691—709.

5.Khokhlova  T.N.,  Kipnis  M.M.  The  breaking  of  a  delayed  ring  neural  network  contributes  to  stability:  The  rule  and  exceptions  //  Neural  Networks  (2013)  V.  48  —  P.  148—152.

6.Zhao  D.-X.,  Wang  J.-M.  Stability  of  a  delayed  ring  neural  network  with  one  small-world  connection,  Chinese  Control  and  Decision  Conference  (CCDC),  Springer,  2011.