ДИСПЕРСИОННАЯ  ИНТЕРПРЕТАЦИЯ  СООТНОШЕНИЯ  НЕОПРЕДЕЛЕННОСТЕЙ  ДЛЯ  ЭНЕРИИ  И  ВРЕМЕНИ  И  КОРОТКОИМПУЛЬСНОЕ  ЛАЗЕРНОЕ  ИЗЛУЧЕНИЕ  В  КВАЗИКЛАССИЧЕСКОМ  ПОДХОДЕ

Давыдов  Александр  Петрович

канд.  физ.-мат.  наук,  доцент  кафедры  прикладной  математики  и  информатики  государственного  технического  университета,  РФ,  г.  Магнитогорск

E-mail: 

DISPERSIVE  INTERPRETATION  OF  THE  UNCERTAITIES  RELATION  FOR  ENERGY  AND  TIME  AND  THE  SHORT-IMPULS  LASER  RADIATION  IN  THE  QUASI-CLASSICAL  APPROACH

Aleksandr  Davydov

candidate  of  Physical  and  Mathematical  Science,  assistant  professor  of  the  Department  of  Applied  Mathematics  and  Informatics  of  Magnitogorsk  State  Technical  University,  Russia  Magnitogorsk

АННОТАЦИЯ

Для  иллюстрации  «дисперсионной»  трактовки  соотношения  неопределенностей  для  энергии  и  времени  рассмотрено  короткоимпульсное  лазерное  излучение  с  позиций  «квазиклассического»  подхода.  Уточняются  критерии  длительности  излучения  и  ее  связь  со  среднеквадратичным  отклонением  момента  времени  наступления  соответствующего  перехода.  Обращается  внимание,  что  в  спектральном  анализе  существенную  роль  могут  сыграть  отрицательные  энергии,  проявив  себя  на  опыте  вполне  реально.

ABSTRACT

For  illustration  of  the  dispersive  interpretation  of  the  energy-time  uncertainty  relation  the  short-time  impulse  laser  radiation  is  discussed  from  the  points  of  view  quasi-classical  approach.  The  criterions  of  radiation  duration  are  précised,  and  also  its  connection  with  root-mean-square  deviation  of  time  moment  of  corresponding  transition  coming.  It’s  proved,  that  in  spectral  analysis  the  negative  energies  are  able  to  play  the  essential  role  and  thus  to  display  themselves  as  if  really  in  experience.

Ключевые  слова:  лазерное  излучение;  неопределенность;  среднее  квадратичное  отклонение;  энергия  и  время  регистрации  фотона;  Планк.

Keywords:  laser  radiation;  the  uncertainty;  standard  deviation;  energy  and  time  of  registration  of  the  photon,  Planck's  constant.

В  статьях  [1,  с.  358],  [2,  с.  323],  [3,  с.  80]  в  рамках  квазиклассического  подхода  к  описанию  электромагнитного  излучения  доказано  соотношение  неопределенностей  для  энергии  и  времени  в  дисперсионной  трактовке

.                                               (1)

Идея  и  необходимость  этого  доказательства  возникли  в  ходе  исследования  эволюции  в  пространстве  и  во  времени  волновых  пакетов,  описывающих  распространение  свободного  фотона.  Волновой  пакет  конструируется  [4,  с.  235],  [5,  с.  269]  из  бивекторов,  собственных  для  операторов  энергии,  импульса  и  спиральности,  и  представляет  собой  одночастичную  волновую  функцию  фотона  в  координатном  представлении  с  традиционной  для  квантовой  механики  интерпретацией:  с  помощью  этой  волновой  функции  можно  предсказать  плотность  вероятности  обнаружить  фотон  в  заданной  точке  конфигурационного  пространства  (локализации  фотона  не  подразумевается).

При  адекватном  к  реальному  излучению  моделировании  эволюции  волновых  пакетов,  когда  одним  из  исходных  параметров  является  время  его  излучения  ,  его  можно  найти  лишь  из  соотношения  неопределенностей  для  энергии  и  времени.  Но  для  этого  нужно  выяснить  физический  смысл  параметра  ,  для  которого  обычно  записывают  «соотношение  неопределенностей»  в  виде

,                                         (2)

где:    —  ширина  линии  излучения  (в  энергетических  единицах).

Если  под    понимать  время  излучения,  то  для  случая  короткоимпульсного  лазерного  излучения  соотношение  (2)  следует  уточнить,  поскольку  оно  дает  ошибку  в  оценке    в  два  раза.  Действительно,  неопределенность  энергии    в  этом  случае  в  (1),  как  будет  показано  ниже,  необходимо  заменить  величиной

,                                              (3)

а  неопределенность    момента  времени  излучения  фотона  —  величиной

.                                             (4)

В  результате,  вместо  традиционно  используемого  приблизительного  равенства  (2),  для  «чисто  квантового»  случая  из  («минимизированного»)  соотношения  неопределенностей  (1)  для  энергии  и  времени  получаем

.                                              (5)

Очевидно,  коррекция  соотношения  (2)  до  более  реального  (5)  имеет  не  только  методический,  но  и  практический  интерес,  когда  речь  идет  об  оценках  длительности  лазерных  импульсов  фемптосекундного  и  менее  диапазонов.

Покажем,  что  для  лазерного  импульса,  излучение  которого  начинается  при  ,  достигает  максимума  при    и  заканчивается  при  ,  следует  считать,  что  среднее  квадратичное  отклонение    момента  времени  излучения  «отдельного»  фотона  подчиняется  формуле  (4),  то  есть  в  2  раза  меньше  времени  излучения  ,  понимаемого  как  продолжительность  того  интервала  времени,  на  протяжении  которого  фотон  с  наибольшей  вероятностью  должен  быть  излучен.  Это  влечет  за  собой  из  (1),  при  осуществлении  связи  (3),  которую  мы  также  установим,  более  уместное  приближенное  равенство  (5).

Для  этого  смоделируем  процесс  лазерного  излучения  зависимостью  от  времени  [80,  с.  3]  напряженностью  электрического  поля  (в  некоторой  области  пространства),  соответственно  «квазиклассическому»  подходу,  в  виде

,                     (6)

где:  ; 

  —  центральная  циклическая  частота  излучения, 

  —  параметр,  характеризующий  длительность  излучения,  амплитуда  и  интенсивность  которого  достигают  максимума  при  .

Если  нас  интересуют  статистические  характеристики  регистрации  фотона  где-либо  на  пути  лазерного  пучка  в  точке    то,  согласно  (6),  центр  волнового  пакета  должен  проходить  через  эту  точку    в  средний  момент  времени  .

В  [1—3]  плотность  потока  энергии  (в  гауссовой  системе)  электромагнитного  излучения  вблизи  точки    пространства  полагалась  равной

,                                   (7)

где:    —  плотность  энергии  вблизи  этой  точки, 

  —  скорость  света  в  вакууме.  Тогда  плотность  вероятности  момента  времени  прохождения  фотона  через  эту  точку    определяется  равенствами

.              (8)

Как  видно,    нормирована  на  единичную  вероятность.  Следовательно,  среднее  значение  момента  времени  прохождения  фотона  через  точку    и  средний  квадрат  этого  момента  времени  соответственно  равны

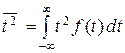,  .                                 (9)

Формулы  (9)  позволяют  найти  дисперсию    и  среднее  квадратичное  отклонение  (неопределенность)  момента  прохождения  фотона  через  точку  :

,  .                                   (10)

Разложим    в  интеграл  Фурье  с  помощью  формул  [1—3]:

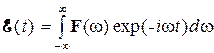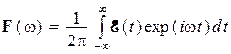,                (11)

и  запишем  соотношение  Парсеваля  (величина  Q  введена  для  удобства):

.                       (12)

Тогда  полную  энергию  излучения,  прошедшую  через  единичную  площадку  за  все  время    от    до  ,  можно  записать  как  интеграл  по    и  по  :

.           (13)

Выражение  (13)  позволяет  ввести  спектральную  плотность  энергии  [1—3]

.                                     (14)

Поделив  (14)  на  (13),  получим  плотность  вероятности  попадания  частоты  излучения  в  интервал    в  окрестности  точки  :

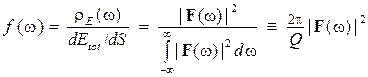.                        (15)

Тогда  средние  значения  частоты  излучения  и  ее  квадрата  вблизи  точки 

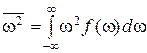,  .                           (16)

Формулы  (16)  позволяют  определить  дисперсию    и  среднее  квадратичное  отклонение  (неопределенность)  частоты  и  энергии  фотона:

,  ,                  (17)

,  .                                    (18)

Формулы  (6)  и  (8)  приводят  к  следующей  плотности  вероятности  момента  времени  прохождения  фотона  через  окрестность  точки  :

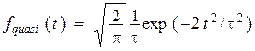.                                (19)

Тогда  из  (9),  (10)  получаем  среднее  квадратичное  отклонение  момента  (неопределенность)  времени  прохождения  фотона  вблизи  точки  :

.                                        (20)

Если  в  качестве  длительности  излучения  использовать  интервал  времени  ,  в  начальный  и  конечный  моменты  ,    которого  интенсивность  излучения  меньше  максимальной  в  2  раза,  то  согласно  (6)  имеем

;  .   (21)

Из  первого  соотношения  (21)  следует  (в  соответствии  с  общепринятой  формулировкой  о  случайных  величинах  с  гауссовским  распределением),  что  если  число  1.18  заменить  единицей,  то  можно  сказать,  что  величины    и    приблизительно  равны  среднему  квадратичному  отклонению    момента  времени  излучения.  При  этом  из  второго  соотношения  (21)  следует,  что  параметр    примерно  равен  времени    излучения.

Применив  формулы  (11)—(18),  получаем:

;                            (22)

;  ;  ;  ;  ;              (23)

.                                           (24)

Стало  быть,  формула  (6)  соответствует  минимизированному  соотношению  неопределенностей  (24),  которое  удовлетворяет  общему  соотношению  (1).

Заметим,  что  для  распределения  (22)  «ширина    на  полувысоте»  действительно  превышает  величину    не  намного  больше,  чем  в  2  раза:

.           (25)

Поэтому,  согласно  (20),  (21),  (24),  связь  длительности  излучения  одного  лазерного  импульса,  понимаемого  как  ,  с  шириной    определяется  более  корректным  приближенным  равенством  (5),  а  не  (2).

Отметим,  что  после  того  как  в  [1—2]  автором  было  доказано  соотношение  (1),  им  было  обнаружено  несколько  ранее  опубликованное  доказательство  (другим  способом)  в  работе  [6].  Однако  в  [6]  оно  получено  «формально-математически»,  без  обсуждения  связи  с  физикой  возможного  вклада  в  спектр  «отрицательных»  частот,  которые  учитывались  в  [6],  но  даже  не  отражались  в  записях  интегралов  по  частотам.  Разумеется,  буквально  отрицательные  частоты  вводить  нельзя.  Однако  если  их  рассматривать  как  математический  множитель  для  отрицательных  энергий  виртуальных  фотонов,  то  формализм  не  изменится.  Важно  то,  что  без  их  учета  соотношение  (1)  невозможно  получить  с  точной  «красивой»  границей  .  Это  указывает  на  то,  что  вклад  отрицательных  энергий  хотя  бы  виртуальных  фотонов  «имеет  право  на  существование».  Некоторые  физические  соображения  по  поводу  возможного  «почти  реального»  проявления  на  опыте  такого  вклада  приведены  в  [3,  с.  87].

Список  литературы:

1.Давыдов  А.П.  Доказательство  соотношения  неопределенностей  для  энергии  и  времени  в  рамках  квазиклассического  подхода  описания  электромагнитных  сигналов  и  излучения  /  А.П.  Давыдов  //  Современные  проблемы  науки  и  образования:  материалы  XLVII  внутривуз.  науч.  конф.  преподавателей  МаГУ.  Магнитогорск:  МаГУ,  2009.  —  С.  358—360.

2.Давыдов  А.П.  Общее  доказательство  соотношения  неопределенностей  для  энергии  и  времени  в  дисперсионной  трактовке  в  квазиклассическом  и  квантовом  случаях  /  А.П.  Давыдов  //  Современные  проблемы  науки  и  образования:  материалы  XLVIII  внутривуз.  науч.  конф.  преподавателей  МаГУ.  Магнитогорск:  МаГУ,  2010.  —  С.  323—325.

3.Давыдов  А.П.  О  соотношении  неопределенностей  для  энергии  и  времени  при  квазиклассическом  описании  электромагнитного  излучения  /  А.П.  Давыдов  //  Фундаментальные  и  прикладные  проблемы  науки.  Том  1.  Материалы  VII  Международного  симпозиума.  М.:  РАН,  2012.  —  С.  80—88.

4.Давыдов  А.П.  Волновая  функция  фотона  в  координатном  представлении  /  А.П.  Давыдов  //  Вестник  МаГУ:  Периодический  научный  журнал.  Вып.  5.  Естественные  науки.  Магнитогорск:  МаГУ,  2004.  —  С.  235—243.

5.Давыдов  А.П.  Эволюция  в  пространстве  и  во  времени  волнового  пакета  фотона  фемптосекундного  излучения  с  точки  зрения  квантовой  механики  /  А.П.  Давыдов  //  Современные  проблемы  науки  и  образования:  Тез.  докл.  XLIII  внутривуз.  науч.  конф.  преподавателей  МаГУ  /  Под  ред.  П.Ю.  Романова  и  Е.М.  Разинкиной.  Магнитогорск:  МаГУ,  2005.  —  С.  269—270.

6.            Полищук  В.И.,  Челкак  С.И.  О  соотношении  неопределенности  для  сигналов  //  Математика  в  ВУЗе,  2006,  №  12.  —  Интернет-журнал  СПбГПУ.  —  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://www.spbstu.ru/publications/m_v/N_012/frame_12.html  (дата  обращения  29.04.2014).