Статья опубликована в рамках: XXXI Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 31 марта 2014 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции, Сборник статей конференции часть II
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
РЕШЕНИЕ ОДНОЙ ДВУХЭТАПНОЙ ЗАДАЧИ НЕЛИНЕЙНОГО СТОХАСТИЧЕСКОГО ПРОГРАММИРОВАНИЯ
Свищикова Марина Владимировна
ассистент кафедры математической теории экономических решений
Санкт-Петербургского государственного университета, РФ, г. Санкт-Петербург
E -mail: marsvi@mail.ru
THE SOLUTION OF NONLINEAR TWO-STAGE STOCHASTIC PROGRAMMING PROBLEM
Svishchikova Marina
teaching fellow of department of Mathematical Theory of Decision Making in Economy St. Petersburg State University, Russia Saint Petersburg
АННОТАЦИЯ
В статье рассматривается задача стохастического программирования с двумя типами случайностей, двумя типами переменных и двумя типами ограничений. Установлены достаточные условия существования конечного решения рассматриваемой задачи. Предложен прямой метод стохастического программирования, основанный на пошаговом вычислении детерминированных программ, получаемых при фиксации случайных величин. Этот процесс вычислительно проще, чем классический прямой метод, основанный на нахождении обобщенного градиента и проекции на допустимое множество.
ABCTRACT
The problem of stochastic programming with two types of randomness, the two types of variables, and the two types of constraints is considered. Sufficient conditions for the existence of the final problem solution are obtained. The direct method for stochastic programming based on incremental computation of deterministic programs by fixing random variables is proposed. This process is more simple for calculations than the classical direct method based on finding the generalized gradient and the projection on the allowable set.
Ключевые слова: стохастическое программирование; выпуклость; прямые методы.
Keywords: stochastic programming; convex; direct methods.
Введение. Целью данной работы является получение эффективного алгоритм решения часто возникающей в экономических моделях двухэтапной задачи стохастического программирования.
Задача-предтеча. Классическая схема интерпретации задачи стохастического программирования (одноэтапной) примерно такая. Описывается нелинейная детерминированная задача с параметрами (задача-предтеча). Далее полагается, что эти параметры — случайные величины. Строится новая детерминированная задача — детерминированный эквивалент. В ней задается целевая функция и ограничения часто с помощью статистических функций типа математического ожидания и дисперсии. Для двухэтапной стохастической задачи пояснительную детерминированную задачу-предтечу, в которой уже были бы два этапа, указать весьма сложно. Вместо этого опишем задачу-предтечу с частичной случайностью.
Минимизировать целевую функцию ![]() общего вида при ограничениях двух типов:
общего вида при ограничениях двух типов:
|
|
(1) |
|
|
(2) |
|
|
(3) |
где ![]() и
и ![]() — наборы параметров задачи,
— наборы параметров задачи, ![]() ,
, ![]() — множество векторных параметров,
— множество векторных параметров, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
|
|
(4) |
Неравенства в (2) и (3) понимаются покомпонентно. Функции ![]() ,
, ![]() и
и ![]() предполагаются при любом значении наборов
предполагаются при любом значении наборов ![]() выпуклыми по первому аргументу в
выпуклыми по первому аргументу в ![]() и непрерывно дифференцируемыми по
и непрерывно дифференцируемыми по ![]() ;
; ![]() — монотонно возрастает по каждой переменной.
— монотонно возрастает по каждой переменной.
Обычная нелинейная программа (1)—(4) резко усложняется после появления времени. Даже если всего два момента.
Формулы этапов. Назовем первым этапом ранний момент, вторым этапом — поздний момент. Будем считать, что на первом этапе известно ![]() и следует выбрать
и следует выбрать ![]() , на втором этапе становится известным
, на втором этапе становится известным ![]() и следует выбрать
и следует выбрать ![]() , а изменить
, а изменить ![]() уже невозможно.
уже невозможно.
Программа (1)—(4) в совокупности с формулами этапов является двухэтапной задачей стохастического программирования (СП2Э). Для нее на втором этапе происходит поиск апостериорного решающего правила (выбор ![]() ), которое суть алгоритм решения следующей нелинейной программы
), которое суть алгоритм решения следующей нелинейной программы
|
|
(5) |
Значительно сложнее 1-й этап. Трактовать его как некоторую нелинейную программу не позволяет нехватка данных (а именно ![]() ). Поэтому первый шаг первого этапа заключается вовсе не в каком-то действии, которое составляет часть алгоритма решения, а в построении новой задачи и определении ее решения. К этому существуют разные подходы, в зависимости от типа параметров
). Поэтому первый шаг первого этапа заключается вовсе не в каком-то действии, которое составляет часть алгоритма решения, а в построении новой задачи и определении ее решения. К этому существуют разные подходы, в зависимости от типа параметров ![]() . Если они интерпретируются как случайные величины с известными распределениями, то традиционно новой целевой функцией назначается математическое ожидание исходной целевой функции
. Если они интерпретируются как случайные величины с известными распределениями, то традиционно новой целевой функцией назначается математическое ожидание исходной целевой функции
|
|
(6) |
Стохастическая программа (1) –(4) является полноценной задачей и далее именно ее и ее модификации будем именовать СП2Э. Под ее решением при некотором ![]() будем понимать совокупность значений целевой функции
будем понимать совокупность значений целевой функции ![]() и минимайзера
и минимайзера ![]() , который представляет собой либо точку минимума, удовлетворяющую (2) и (3), либо минимизирующую последовательность
, который представляет собой либо точку минимума, удовлетворяющую (2) и (3), либо минимизирующую последовательность ![]() такую, что
такую, что
|
|
|
|
|
|
Здесь ![]() eсть минимайзер нелинейной программы (5) при
eсть минимайзер нелинейной программы (5) при ![]() .
.
Под общим решением двухэтапной задачи понимается совокупность минимайзеров программ (5) и (6) и значений целевых функций ![]() и
и ![]() . Минимайзер
. Минимайзер ![]() и, именуемый решающим правилом минимайзер
и, именуемый решающим правилом минимайзер ![]() , имеют различную временную активность:
, имеют различную временную активность: ![]() — от момента решения (5) до появления информации об
— от момента решения (5) до появления информации об ![]() , правило
, правило ![]() – после получения
– после получения![]() .
.
Рассмотрим набор ![]() . Пусть в нем присутствуют параметры двух типов. В один тип входят такие случайные факторы, как спрос, погода, выход из строя оборудования и т. п. Они относятся к будущему. В другой — величины детерминированные, но известные неточно, такие как численность трудящихся, объем месторождения и т. п. Они относятся к прошлому или настоящему. Так же как и в первом типе, эти величины удобно трактовать как случайные с известными параметрами распределения. Известные же точно компоненты набора
. Пусть в нем присутствуют параметры двух типов. В один тип входят такие случайные факторы, как спрос, погода, выход из строя оборудования и т. п. Они относятся к будущему. В другой — величины детерминированные, но известные неточно, такие как численность трудящихся, объем месторождения и т. п. Они относятся к прошлому или настоящему. Так же как и в первом типе, эти величины удобно трактовать как случайные с известными параметрами распределения. Известные же точно компоненты набора ![]() ничего нового не вносят в постановку задачи. Исключим их, отнеся просто к виду функций.
ничего нового не вносят в постановку задачи. Исключим их, отнеся просто к виду функций.
Взаимосвязь между наборами ![]() ,
, ![]() и ограничениями (2) и (3) различна. Ограничения (3) должны выполняться при любой мыслимой реализации параметров (таково, например, ограничение числа пассажиров в такси). Иными словами, необходимо соблюдать при каждой случайной реализации условий задачи общие физические ограничения системы, которых нельзя нарушать вообще. Ограничения (2) должны выполняться в среднем (как, например, требование достаточной заполняемости конкретных авиарейсов, для того чтобы данное направление имело доходность и не было убыточным). Иными словами, необходимо, чтобы долговременные договорные обязательства в целом (поставки сырья и производство продукции, прибыль и т. п.) были удовлетворены, хотя при этом допускаются нарушения в кратковременных требованиях. Поэтому условие (2) вполне естественно заменить на
и ограничениями (2) и (3) различна. Ограничения (3) должны выполняться при любой мыслимой реализации параметров (таково, например, ограничение числа пассажиров в такси). Иными словами, необходимо соблюдать при каждой случайной реализации условий задачи общие физические ограничения системы, которых нельзя нарушать вообще. Ограничения (2) должны выполняться в среднем (как, например, требование достаточной заполняемости конкретных авиарейсов, для того чтобы данное направление имело доходность и не было убыточным). Иными словами, необходимо, чтобы долговременные договорные обязательства в целом (поставки сырья и производство продукции, прибыль и т. п.) были удовлетворены, хотя при этом допускаются нарушения в кратковременных требованиях. Поэтому условие (2) вполне естественно заменить на
|
|
(7) |
После введения случайностей в ![]() и
и ![]() решение задачи (6) становится случайным, что делает эту задачу как модель каких-то реальных событий неадекватной. Такая ситуация уже рассматривалась при обсуждении 1-го этапа задачи СП2Э. Естественно разрешать ее аналогично, т.е. построением новой задачи схожим образом. А именно, считать оптимальным решение нелинейной стохастической программы
решение задачи (6) становится случайным, что делает эту задачу как модель каких-то реальных событий неадекватной. Такая ситуация уже рассматривалась при обсуждении 1-го этапа задачи СП2Э. Естественно разрешать ее аналогично, т.е. построением новой задачи схожим образом. А именно, считать оптимальным решение нелинейной стохастической программы
|
|
(8) |
Программа (8) часто именуется детерминированным эквивалентом задачи (1)—(4), в которой всем параметрам придан случайный характер. (Как следует из вышеизложенного, слово «эквивалент» уместно лишь в переходе от (2) к (8) и совсем не подходит к связи между задачами (7) и (1)—(4).)
Решающее правило для второго этапа. Естественным образом вытекающее из природы функции ![]() требование ее монотонного возрастания по каждому аргументу не только обеспечивает существование минимайзера нелинейной программы (5), но и позволяет его легко найти.
требование ее монотонного возрастания по каждому аргументу не только обеспечивает существование минимайзера нелинейной программы (5), но и позволяет его легко найти.
Введем операцию срезки:
|
|
(9) |
Тогда, очевидно, искомый минимайзер (решающее правило) имеет вид
|
|
(10) |
Применяя его в программе (8), получаем
|
|
(11) |
2. Существование решения двухэтапной задачи стохастического программирования (11).
В дальнейшем потребуется следующий результат.
Лемма 1. Пусть функция ![]() равномерно непрерывна по
равномерно непрерывна по ![]() . Тогда функция
. Тогда функция
|
|
|
(![]() — плотность вероятности) непрерывна.
— плотность вероятности) непрерывна.
Д о к а з а т е л ь с т в о. Согласно равномерной непрерывности функции ![]() ,
,
|
|
|
Выберем такие ![]() и
и ![]() . Тогда
. Тогда
|
|
|
Теорема 1 (О существовании конечного решения задачи). Пусть
1. ![]() задана на
задана на ![]() ;
;
2. множество ![]() — непусто и ограничено;
— непусто и ограничено;
3. ![]() ,
, ![]() заданы и непрерывны по
заданы и непрерывны по ![]() на
на ![]() ,
, ![]() равномерно непрерывна по
равномерно непрерывна по ![]() на
на ![]() ;
;
4. ![]() задана и непрерывна на
задана и непрерывна на ![]() , и монотонно возрастает по каждой компоненте
, и монотонно возрастает по каждой компоненте ![]() . (
. (![]() – см. (9).)
– см. (9).)
Тогда существует конечное решение детерминированного эквивалента (11). Если множество ![]() неограничено, то конечного решения может и не быть.
неограничено, то конечного решения может и не быть.
Д о к а з а т е л ь с т в о. Лемма 1 дает непрерывность ![]() , что в свою очередь влечет замкнутость множества
, что в свою очередь влечет замкнутость множества ![]() . В сочетании с условием (2) это дает возможность применить теорему Кантора о том, что на замкнутом ограниченном множестве конечномерного пространства непрерывная функция равномерно непрерывна. Получаем равномерную непрерывность по
. В сочетании с условием (2) это дает возможность применить теорему Кантора о том, что на замкнутом ограниченном множестве конечномерного пространства непрерывная функция равномерно непрерывна. Получаем равномерную непрерывность по ![]() функции
функции ![]() и
и ![]() при любых
при любых ![]() . Из Леммы 1 следует непрерывность
. Из Леммы 1 следует непрерывность ![]() на
на ![]() . Поэтому замкнутость и ограниченность
. Поэтому замкнутость и ограниченность ![]() влечет существование в нем конечного минимайзера функции
влечет существование в нем конечного минимайзера функции ![]() .
. ![]()
3. Итеративный алгоритм решения задачи (11).
В предположении, что функции ![]() ,
, ![]() и
и ![]() — непрерывны по
— непрерывны по ![]() и
и ![]() монотонно возрастает по каждой компоненте
монотонно возрастает по каждой компоненте ![]() , задача (11) может быть решена прямым итеративным алгоритмом.
, задача (11) может быть решена прямым итеративным алгоритмом.
Шаг 0. Задается ![]() , натуральное число
, натуральное число ![]() , выбирается из каких-то дополнительных соображений начальная точка
, выбирается из каких-то дополнительных соображений начальная точка ![]() и назначается
и назначается ![]() ,
, ![]() ,
,![]() . Шаг 1. Генерируется случайный вектор
. Шаг 1. Генерируется случайный вектор ![]()
Шаг 2. Любым способом решается относительно ![]() нелинейная программа
нелинейная программа
|
|
(12) |
где выбор весов ![]() производится согласно аксиомам (13)—(15).
производится согласно аксиомам (13)—(15).
Шаг 3. Если ![]() , то {
, то {![]() ; перейти на Шаг 4}.
; перейти на Шаг 4}.
|
|
|
Если ![]() , то {вывод
, то {вывод ![]() ; выход из алгоритма}.
; выход из алгоритма}.
Шаг 4. Полагается ![]() ;
; ![]() . Переход к Шагу 1.
. Переход к Шагу 1.
Пояснения к алгоритму.
Формирование весов. Веса ![]() будем выбирать классическим образом [1, 3, 5, 6] согласно аксиомам:
будем выбирать классическим образом [1, 3, 5, 6] согласно аксиомам:
|
|
|
(13) |
|
|
(14) |
|
|
|
(15) |
|
Такие веса существуют. Например, ![]() . Они обеспечивают, с одной стороны, возможность уйти от «начальной» точки
. Они обеспечивают, с одной стороны, возможность уйти от «начальной» точки ![]() к решению задачи (11), сколь далеко бы от «начальной» точки оно ни находилось (аксиома (15)). C другой стороны, из аксиомы (14) следует, что
к решению задачи (11), сколь далеко бы от «начальной» точки оно ни находилось (аксиома (15)). C другой стороны, из аксиомы (14) следует, что
|
|
(16) |
Пусть ![]() — последовательность итераций, порождаемая приведенным алгоритмом с «выключенным» выходом на Шаге 3. Оказывается, если она содержит монотонно сходящуюся к некоторой точке
— последовательность итераций, порождаемая приведенным алгоритмом с «выключенным» выходом на Шаге 3. Оказывается, если она содержит монотонно сходящуюся к некоторой точке ![]() подпоследовательность
подпоследовательность ![]() такую, что
такую, что ![]() ,
, ![]() то сама сходится к
то сама сходится к ![]() . Сходимость, возможно, не монотонная, но увеличение расстояния от
. Сходимость, возможно, не монотонная, но увеличение расстояния от ![]() до
до ![]() , когда индекс
, когда индекс ![]() пробегает значения от
пробегает значения от ![]() до
до ![]() не превосходит
не превосходит
|
|
|
Отсюда,
|
|
|
т. е. «колебания» элементов последовательности ![]() относительно
относительно ![]() в асимптотике будут стремиться к нулю. Естественное требование смещения от текущей итеративной точки в направлении полученного минимума содержится в аксиоме (13).
в асимптотике будут стремиться к нулю. Естественное требование смещения от текущей итеративной точки в направлении полученного минимума содержится в аксиоме (13).
Правило остановки (Шаг 3). Зададимся конечной погрешностью ![]() . После
. После
t -ой итерации сделаем еще столько шагов, чтобы их суммарная длина превосходила ![]() в
в ![]() раз. Другими словами,
раз. Другими словами,
|
|
|
Если при этом все итерации от i-ой до (i+N)-ой остаются в шаре радиуса ![]() с центром
с центром ![]() , т. е.
, т. е. ![]() , то на этом заканчивается итеративный процесс. В качестве ответа можно взять последнюю итеративную точку из множества
, то на этом заканчивается итеративный процесс. В качестве ответа можно взять последнюю итеративную точку из множества ![]() .
.
Теорема 2. Алгоритм Шаг 1—Шаг 4 с выбором весов согласно аксиомам (13)—(15) сходится.
Д е й с т в и т е л ь н о, поскольку разность ![]() соответствует обобщенному градиенту, приведенный алгоритм с указанным выбором весов подпадает под действие теоремы Ю.М. Ермольева [1], что обеспечивает сходимость этого алгоритма.
соответствует обобщенному градиенту, приведенный алгоритм с указанным выбором весов подпадает под действие теоремы Ю.М. Ермольева [1], что обеспечивает сходимость этого алгоритма.![]()
4. Заключение. Предлагаемый итеративный алгоритм вполне адекватен рассматриваемой задаче. Его сходимость имеет и некоторые недостатки, присущие сходимости классических прямых методов стохастического программирования, в частности замедление сходимости с возрастанием индекса шага итерации. Преимущество по сравнению с ними видится в более легком пошаговом решении линейной программы (12), чем вычисление обобщенного градиента с последующим нахождением проекции на допустимое множество [1, 2, 3].
Список литерературы:
1.Ермольев Ю.М. Методы стохастического программирования. М.: Наука, 1976. — 340 c.
2.Ермольев Ю.М., Ляшко И.И., Михалевич В.С., Тюпля В.И. Математические методы исследования операций. М.: Наука, 1979. — 312 c.
3.Ермольев Ю.M., Норкин В.И. Методы решения невыпуклых негладких задач стохастической оптимизации // Кибернетика и системный анализ. — 2003. — № 5. — С. 89—106.
4.Kolbin V.V. Stochastic programming. Holland-USA: D. Reidel Publ. C., 1977. — 325 p.
5.Поляк Б.Т. Введение в оптимизацию. М.: Наука, 1979. — 384 с.
6.Юдин Д.Б. Математические методы управления в условиях неполной информации. М.: Сов. радио, 1974. — 400 с.
дипломов


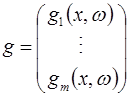 ,
, 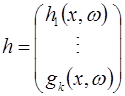 ,
, 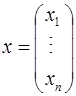 ,
, 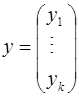
 .
. .
.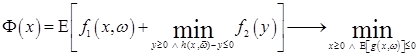 .
.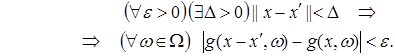
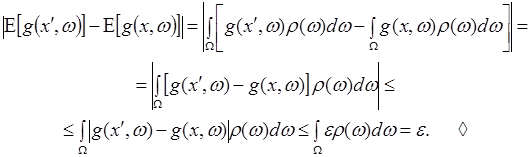
 .
.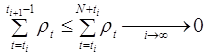 .
.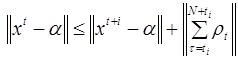 ,
,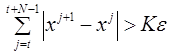 .
.
Оставить комментарий