МОДЕЛИРОВАНИЕ  ТЕПЛОВЫХ  ПРОЦЕССОВ  ПРИ  ПЛАЗМЕННО-ДУГОВОЙ  НАПЛАВКЕ  ЦИЛИНДРИЧЕСКИХ  ЗАГОТОВОК

Прохоров  Александр  Владимирович

канд.  техн.  наук,  доцент,  филиал  федерального  государственного  бюджетного  образовательного  учреждения  высшего  профессионального  образования  «Южно-Уральский  государственный  университет»  (национальный  исследовательский  университет)  в  г.  Озерске,  РФ,  г.  Озерск

E-mail: 

MODELLING  OF  THERMAL  PROCESSES  IN  CASE  OF  PLASMA-ARC  SURFACING  OF  CYLINDRICAL  BLANKS

Aleksandr  Prokhorov

candidate  of  engineering  sciences,  associate  professor  of  branch  of  FSBEI  HVE  National  Research  South  Ural  State  University  in  Ozersk,  Russia  Ozersk

АННОТАЦИЯ

В  статье  предложена  аналитическая  методика  определения  температурных  полей  в  цилиндрической  заготовке  при  плазменно-дуговой  наплавке  с  учетом  теплоотдачи  с  поверхности  обрабатываемого  металла;  по  полученным  соотношениям  проведен  расчет  температуры  в  цилиндре,  обрабатываемом  электрической  дугой.

ABSTRACT

In  the  article  there  is  proposed  an  analytical  method  of  temperature  fields’  determination  in  a  cylindrical  blank  in  case  of  plasma-arc  surfacing  with  regard  to  the  heat  transmission  from  the  surface  of  the  processed  metal.  According  to  the  obtained  correlations  temperature  calculation  has  been  performed  in  a  cylinder  exposed  by  an  electric  arc.

Ключевые  слова:   математическое  моделирование;  температурное  поле;  нагрев;  теплопередача.

Keywords:   mathematical  modelling;  temperature  field;  heating;  heat  transmission. 

Процесс  резания  сверхпрочных  марок  стали  характеризуется  большими  тепловыми  и  силовыми  нагрузками  на  режущий  инструмент.  Вследствие  этого  снижается  его  стойкость,  увеличивается  время,  затрачиваемое  на  обработку  одной  детали,  растут  мощность,  габариты  и  вес  станков  [6].

Процесс  плазменно-механической  обработки  позволяет  повысить  весовую  производительность  процесса  резания,  то  есть  массу  стружки,  снимаемой  с  заготовки  в  единицу  времени.  Плазменно-механическая  обработка  —  это  комбинированный  способ  формообразования  деталей,  включающий  подогрев  срезаемого  слоя  сильноточной  стабилизированной  дугой  и  его  последующее  удаление  режущим  инструментом  [5,  8].  Обрабатываемая  деталь  при  этом,  как  правило,  является  анодом.

Использование  сильноточной  стабилизированной  дуги  имеет  следующие  преимущества  перед  другими  видами  нагрева:  высокая  пространственно-временная  устойчивость  столба  дуги  и  прианодной  области,  большая  концентрация  потока  энергии  на  поверхности  обрабатываемого  материала,  удобство  регулирования  мощности  потока  плазмы  [1].

Проведенные  эксперименты  [2]  показали,  что  вводимый  в  анод  тепловой  поток  в  пятне  нагрева  подчиняется  закону  нормального  распределения.  Анализ  экспериментальных  распределений  позволяет  сказать,  что  за  характерный  размер  гауссова  источника  можно  брать  радиус  сопла  плазмотрона. 

Кроме  того,  в  [2]  приведены  номограммы  для  определения  распределения  температуры  по  глубине  изделия  при  электродуговом  нагреве.  Выявлено,  что  определяющим  фактором  длительности  пребывания  металла  в  области  высоких  температур  является  скорость  перемещения  источника  энергии.

Знание  распределения  температуры  в  обрабатываемой  заготовке  позволяет  судить  о  структурных  превращениях  в  материале  и  изменениях  его  механических  характеристик  [3,  4,  7].

Следует  отметить,  что  определение  температуры  заготовки  по  таблицам  и  номограммам  по  информативности  и  удобству  заимствования  значительно  уступает  аналитическим  инженерным  формулам,  позволяющим  проводить  расчеты  температурных  полей  для  любой  точки  изделия  независимо  от  типа  и  вида  моделируемого  источника.

При  разработке  аналитического  метода  расчета  предполагается,  что  источник  тепла  (опорное  пятно  дуги)  является  быстроперемещающимся  в  направлении  окружной  скорости,  температура  по  окружности  практически  не  изменяется,  и  пятно  нагрева  эквивалентно  по  своему  действию  кольцевому  источнику  тепла. 

В  пользу  этого  предположения  говорит  то  обстоятельство,  что  при  малой  продольной  подаче  (»  1  мм/с)  и  относительно  большом  числе  оборотов  заготовки  (2  ¸  5  об/с)  опорное  пятно  плазменной  дуги  пробегает  несколько  раз  практически  по  одной  и  той  же  поверхности,  которая  при  этом  не  успевает  значительно  остыть  и  имеет  температуру,  близкую  к  температуре  плавления  металла  заготовки.

В  [6]  быстродвижущийся  источник  теплоты,  моделирующий  действие  электрической  дуги,  перемещается  по  поверхности  цилиндра  по  винтовой  линии  малого  шага.  Температура  в  заданной  точке  тела  находится  как  сумма  температур  от  действия  мгновенных  линейных  круговых  источников,  расположенных  на  указанной  винтовой  линии.  При  большом  числе  витков  расчет  температуры  значительно  усложняется  и  требуется  переход  к  другой  модели  источника.

В  данной  работе  тепловое  действие  движущейся  электрической  дуги  моделируется,  в  отличие  от  [1,  3],  одним  круговым  нормально  распределенным  источником. 

Источник  перемещается  вдоль  цилиндра  со  скоростью,  равной  ,  где    —  частота  вращения  обрабатываемой  детали,    —  шаг  винтовой  линии,  по  которой  ведется  наплавка  материала.

Из  дифференциального  уравнения  энергии  для  перемещающегося  цилиндрического  тела  при  граничных  условиях  третьего  рода  по  методике,  описанной  в  работах  [4,  5]  получена  формула  для  расчета  температурного  поля  в  любой  точке  нагреваемой  заготовки:

,

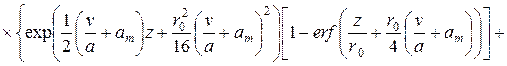
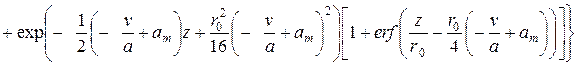где:    —  приращение  температуры;

  —  температуропроводность  стали;

  —  теплопроводность  материала  детали;

  —  радиус  заготовки; 

  —  гипергеометрическая  функция; 

  —  цилиндрические  координаты; 

  —  корни  характеристического  уравнения; 

  —  функции  Бесселя  первого  рода  нулевого  и  первого  порядка; 

;

  —  характерный  размер  источника  теплоты; 

  —  эффективная  тепловая  мощность  источника; 

  —  интеграл  ошибок; 

  —  показатель  степени  отношения  ,  входящего  в  функцию  источников  теплоты.

Расчет  температуры  в  стальной  цилиндрической  заготовке  (вале)  проведен  при  следующих  исходных  данных:  =1×10^-5  м²/с;  =40  Вт/(м×К);  =0,05  м;  =3×10^-4  м/с;  =5×10^-3  м;  =100;  =2×10³  Вт.

Результаты  расчета  показали,  что  при    положение  максимума  температуры  не  совпадает  с  началом  координат  (центром  источника);  с  уменьшением    это  несовпадение    увеличивается  и  достигает  наибольшей  величины  при  =0.  С  ростом  скорости  перемещения  источника    также  увеличивается.

Большой  перепад  температуры  вблизи  источника,  обусловленный  отводом  тепла  в  направлении  осей    и    может  привести  к  закалке  поверхностного  слоя  детали  (для  сталей  типа  25ХГСА-35ХГСА),  что  скажется  на  характере  окончательной  механической  обработки  вала.

Список  литературы:

1.Буланый  П.Ф.  Оптимизация  нагрева  металла  электрической  дугой  /  П.Ф.  Буланый,  С.П.  Поляков  //  ИФЖ.  —  1980.  —  Т.  39,  —  №  4.  —  С.  687—691.

2.Киселев  Ю.Я.,  Исследование  радиального  распределения  плотности  теплового  потока  в  опорных  пятнах  плазменной  режущей  дуги  /  Ю.Я.  Киселев,  В.К.  Погора  //  ИФЖ.  —  1990.  —  Т.  56,  —  №  6.  —  С.  892—896.

3.Осовец  С.В.  Расчет  нестационарного  теплового  состояния  плиты  при  ее  нагреве  перемещающимся  источником  /  С.В.  Осовец,  Е.В.  Торопов,  А.В.  Прохоров,  В.Л.  Кириллов  //  Инженерно-физический  журнал.  —  2000.  —  Т.  73,  —  №  4.  —  С.  757—760.

4.Пашацкий  Н.В.  Тепловые  процессы  при  обработке  предварительно  нагретой  стальной  плиты  огневой  машиной  /  Н.В.  Пашацкий,  А.В.  Прохоров  //  Известия  ВУЗов.  Черная  металлургия.  —  2001.  —  №  3.  —  С.  46—48.

5.Пашацкий  Н.В.  Аналитическая  модель  нагрева  заготовки  при  плазменно-механической  обработке  /  Н.В.  Пашацкий,  А.В.  Прохоров  //  Технология  машиностроения.  —  2002.  —  №  1.  —  С.  8—9.

6.Строшков  А.Н.  Обработка  резанием  труднообрабатываемых  материалов  с  нагревом  /  А.Н.  Строшков.  М.:  Машиностроение,  1977.

7.Теория  сварочных  процессов  /  Под  ред.  В.В.  Фролова.  М.:  Высшая  школа,  1988.  —  559  с.

8.Шатерин  М.А.  Эффективность  нагрева  заготовки  при  плазменно-механической  обработке  /  М.А.  Шатерин,  А.Л.  Попилов,  В.С.  Медко  //  Сварочное  производство.  —  1982.  —  №  5.  —  С.  29—30.