Статья опубликована в рамках: XXX Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 26 февраля 2014 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции, Сборник статей конференции часть II
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
РЕШЕНИЕ ОБЩЕЙ ЗАДАЧИ ТЕРМОКАРОТАЖА ДЛЯ СЛУЧАЯ ПОСТОЯННЫХ ГРАДИЕНТОВ В НУЛЕВОМ ПРИБЛИЖЕНИИ
Филиппов Александр Иванович
профессор филиала ФГБОУ ВПО УГНТУ в г. Салавате, РФ, Республика Башкортостан, г. Салават
E -mail: filippovai@rambler.ru
Бикзянова Альбина Аликовна
студент филиала ФГБОУ ВПО УГНТУ в г. Салавате, РФ, Республика Башкортостан, г. Салават
E -mail: bikzyanov2000@mail.ru
Родионов Артём Сергеевич
ассистент филиала ФГБОУ ВПО УГНТУ в г. Салавате, РФ, Республика Башкортостан, г. Салават
SOLVING THE COMMON PROBLEM OF TEMPERATURE WELL LOGGING FOR CASE OF CONSTANT GRADIENT IN ZERO APPROXIMATION
Filippov Aleksandr
professor of branch in Ufa State Petroleum Technological University in Salavat, Russian Federation, Republic of BashkortostanSalavat
Bikzyanova Albina
student of branch in Ufa State Petroleum Technological University in Salavat, Russian Federation, Republic of BashkortostanSalavat
Rodionov Artem
assistant of branch in Ufa State Petroleum Technological University in Salavat, Russian Federation, Republic of BashkortostanSalavat
АННОТАЦИЯ
На основе «в среднем точного» асимптотического метода, построено решение задачи о нестационарном теплообмене в скважинах в предположении постоянства вертикальных градиентов температуры в нулевом приближении для потока жидкости и среды, окружающей скважину. Произведен учет вклада режима течения в температурные поля. Проведено обезразмеривание задачи и переход в пространство изображений Лапласа-Карсона.
ABSTRACT
Based on the "average exact" asymptotic method, constructed solution of the problem of unsteady heat transfer in wells assuming a constant vertical temperature gradients in the zero approximation for fluid flow and the environment surrounding the well. Produced account the contribution of the flow regime in the temperature field. Held dimensionless problem and the transition to the image space of the Laplace-Carson.
Ключевые слова : градиент; скважина; турбулентный поток.
Keywords : gradient; well; turbulent flow.
Не подлежит сомнению, что одной из важнейших фундаментальных направлений современной науки является исследование турбулентного движения жидкости. Проблема построения теории турбулентного движения жидкости крайне актуальна для нефтедобычи. Задача о температурном поле турбулентного потока в скважине существенно упрощается, если предположить постоянство вертикальных градиентов, что сравнительно часто реализуется на практике.
Предположение постоянства градиентов температуры ![]() приводит к тому, что вторые производные по вертикальной координате, как в скважине, так и в окружающей среде обращаются в нуль. Первым этапом решения является параметризация задачи, которая осуществляется формальной заменой
приводит к тому, что вторые производные по вертикальной координате, как в скважине, так и в окружающей среде обращаются в нуль. Первым этапом решения является параметризация задачи, которая осуществляется формальной заменой ![]() на
на ![]() как в уравнении для температуры потока в стволе скважины, так и в граничном условии. Постановка безразмерной параметризованной задачи для температуры в скважине
как в уравнении для температуры потока в стволе скважины, так и в граничном условии. Постановка безразмерной параметризованной задачи для температуры в скважине ![]() и окружающей среде
и окружающей среде ![]() в этом случае имеет вид
в этом случае имеет вид
|
|
(1) |
|
|
(2) |
|
|
(3) |
|
|
(4) |
|
|
(5) |
|
|
(6) |
Представление задачи в безразмерных переменных осуществлено с помощью следующих формул: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , где a1 — коэффициент температуропроводности окружающей среды, м2/с; с, с1 — удельная теплоемкость флюида и окружающей среды соответственно, Дж/(К·кг); D — глубина скважины, м; Ре — аналог параметра Пекле; rd, zd, и r, z — размерные и безразмерные цилиндрические координаты соответственно, м; r0 — радиус трубы, м; Q(r, z, Fo) — безразмерная функция источников; qd — плотность источников тепла, Вт/м3; T — безразмерная температура флюида; T1 — безразмерная температура среды; t, Fo — размерное и безразмерное время, с; v — средняя скорость жидкости в трубе, м/с; Г — геотермический градиент, К/м; ε — параметр асимптотического разложения; η — адиабатический коэффициент, К/Па; θ, θ1 — температура флюида и окружающей среды соответственно, К; θ01 — естественная невозмущенная температура, К; λ, λ1 — коэффициент теплопроводности потока и окружающей среды, Вт/(м·К); ρ, ρ1 — плотность флюида и окружающей среды, кг/м3.
, где a1 — коэффициент температуропроводности окружающей среды, м2/с; с, с1 — удельная теплоемкость флюида и окружающей среды соответственно, Дж/(К·кг); D — глубина скважины, м; Ре — аналог параметра Пекле; rd, zd, и r, z — размерные и безразмерные цилиндрические координаты соответственно, м; r0 — радиус трубы, м; Q(r, z, Fo) — безразмерная функция источников; qd — плотность источников тепла, Вт/м3; T — безразмерная температура флюида; T1 — безразмерная температура среды; t, Fo — размерное и безразмерное время, с; v — средняя скорость жидкости в трубе, м/с; Г — геотермический градиент, К/м; ε — параметр асимптотического разложения; η — адиабатический коэффициент, К/Па; θ, θ1 — температура флюида и окружающей среды соответственно, К; θ01 — естественная невозмущенная температура, К; λ, λ1 — коэффициент теплопроводности потока и окружающей среды, Вт/(м·К); ρ, ρ1 — плотность флюида и окружающей среды, кг/м3.
Заметим, что постановка задачи осложнена переменными коэффициентами ![]() и
и ![]() , которые для турбулентного потока рассчитываются из уравнений Сполдинга [2].
, которые для турбулентного потока рассчитываются из уравнений Сполдинга [2].
В соответствии с концепцией «в среднем точного» асимптотического метода [4, 3], решение задачи (1)—(6) отыскивается в виде асимптотических формул по параметру ε.
|
|
(7) |
Запишем окончательную постановку задачи в нулевом приближении
|
|
(8) |
|
|
(9) |
|
|
(10) |
|
|
(11) |
|
|
(12) |
Приведенная задача отличается от классических наличием следа производной решения для внешней области в уравнении (9).
Используя преобразования Лапласа-Карсона [1], запишем задачу (8)—(12) в пространстве изображений
|
|
(13) |
|
|
(14) |
|
|
(15) |
|
|
(16) |
Решение задачи в нулевом приближении в пространстве изображений Лапласа-Карсона представлено как
|
|
(17) |
· в скважине,
|
|
(18) |
· в окружающей среде. Здесь 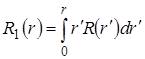 ,
,  ,
, ![]() =
= ![]() . Выражения (17) и (18) представляют решение задачи в нулевом приближении в пространстве изображений.
. Выражения (17) и (18) представляют решение задачи в нулевом приближении в пространстве изображений.
Итак, рассмотрен частный случай задачи о нестационарном теплообмене в скважинах, учитывающей в общем виде вклад режима течения в температурные поля, в котором постулируется постоянство вертикальных градиентов температуры.
Достигнутое на основе развитого авторами метода, снижение порядка производных по радиальной координате позволило построить простое аналитическое решение задачи сопряжения для уравнений, содержащих переменные коэффициенты, в нулевом приближении.
Список литературы:
1.Диткин В.А., Прудников А.П. Справочник по операционному исчислению М.: Высшая школа. 1965. — 466 с.
2.Кэйс В.М. Конвективный тепло- и массообмен. М.: Энергия, 1972. — 448 с.
3.Филиппов А.И. Температурное поле турбулентного потока в скважине / А.И. Филиппов, О.В. Ахметова, А.С. Родионов // Теплофизика высоких температур. — 2013. — Т. 51. — № 2 — С. 277—286.
4.Filippov A.I. Quasi-One-Dimensional Nonstationary Temperature Field of a Turbulent Flow in a Well / A.I. Filippov, O.V. Akhmetova, A.S. Rodionov // Journal of Engineering Thermophysics. — 2012. — Vol. 21. — № 3. — P. 167—180.
дипломов


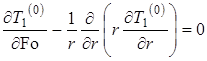 ,
, 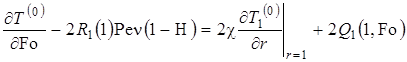 ,
, 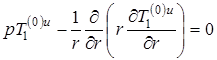 ,
, 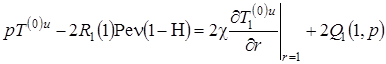 ,
,  ,
,  ,
,
Оставить комментарий