Статья опубликована в рамках: XXX Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 26 февраля 2014 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции, Сборник статей конференции часть II
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
Актуальность
НУЛЕВОЕ АСИМПТОТИЧЕСКОЕ ПРИБЛИЖЕНИЕ ЗАДАЧИ О ФИЛЬТРАЦИОННО-ВОЛНОВОМ ПОЛЕ В ПОРИСТОЙ СРЕДЕ
Филиппов Александр Иванович
д-р техн. наук, профессор СФ БашГУ, РФ, Республика Башкортостан, г. Стерлитамак
E-mail : filippovai@rambler.ru
Ахметова Оксана Валентиновна
канд. физ.-мат. наук, доцент СФ УГНТУ, РФ, Республика Башкортостан, г. Салават
E-mail : ahoksana@yandex.ru
Ковальский Алексей Алексеевич
советник ректора БашГУ, РФ, Республика Башкортостан, г. Уфа
E-mail : aakov68@mail.ru
Юсупова Лениза Рауфовна
студент СФ УГНТУ, РФ, Республика Башкортостан, г. Салават
ZERO ASYMPTOTIC APPROXIMATION OF THE PROBLEM OF FILTRATION-WAVE FIELD IN POROUS MEDIUM
Aleksandr Filippov
doctor of engineering sciences , professor of Sterlitamak branch of Bashkir State University, Republic of Bashkortostan Sterlitamak
Oksana Akhmetova
candidate of Physical and Mathematical Sciences , associate professor of Salavat branch of Ufa State Petroleum Technological University, Republic of Bashkortostan Salavat
Aleksey Kovalskiy
advisor to the rector of Bashkir State University, Republic of Bashkortostan Ufa
Leniza Yusupova
student of Salavat branch of Ufa State Petroleum Technological University, Republic of Bashkortostan
Salavat
АННОТАЦИЯ
С использованием эффективной модификации асимптотического метода, разработанной для решения задач с граничными условиями IV рода, решена задача о фильтрационно-волновых полях давления в слоисто-неоднородной анизотропной среде. Показано, что нулевой коэффициент асимптотического разложения представляет собой эквивалентную цилиндрическую волну давления.
ABSTRACT
Using an effective modification of the asymptotic method developed for solving problems with conjugating boundary conditions the problem of filtration-pressure wave fields in layered inhomogeneous anisotropic medium has been solved. It is shown that a zero coefficient of the asymptotic expansion is the equivalent cylindrical wave of pressure.
Ключевые слова: Нулевой коэффициент разложения; фильтрация; анизотропная среда; осевая симметрия; асимптотический метод
Keywords: zero expansion coefficient; filtration; anisotropic medium; axial symmetry; asymptotic method.
Перспективным направлением интенсификации добычи нефти и газа из недр является использование пороховых термогазогенераторов для обработки призабойной зоны пласта в связи с высокой эффективностью и относительно низкой стоимостью. Однако совершенствование технологии порохового воздействия предполагает развитие теории волновых полей в нефтяных пластах.
1. Постановка задачи для цилиндрической геометрии. На рисунке 1 представлена геометрия течения в цилиндрической системе координат, ось zd которой совпадает с осью скважины. Пусть неоднородная среда представлена тремя областями с плоскими границами раздела zd = ±h, перпендикулярными вертикальной оси. Покрывающий и подстилающий пласты считаются слабопроницаемыми в горизонтальном направлении, средняя область толщины 2h (-h < zd < h) является хорошо проницаемой и в горизонтальном и в вертикальном направлениях. Для простоты течение полагается линейным (по горизонтальной координатной линии rd). Окружающие породы являются сильно анизотропными, и в них преобладает вертикальная проницаемость в сравнении с горизонтальной настолько, что можно пренебречь членом со второй производной по горизонтальной координате rd в уравнении для окружающей среды. Далее положим, что свойства подстилающих и покрывающих пластов идентичны. В соответствии с этим постановку задачи можно упростить, воспользовавшись условием симметрии ![]() .
.
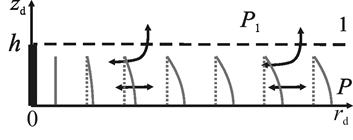
Рисунок 1. Геометрия задачи
Математическая постановка гидродинамической задачи для амплитуд давления в таких предположениях представится в виде [2, 3]
|
|
(1.1) |
|
|
(1.2) |
|
|
(1.3) |
|
|
(1.4) |
|
|
(1.5) |
Предполагается, что решение является регулярным на бесконечности, т. е. при устремлении пространственных координат в бесконечность искомое решение, а при необходимости и его производная, обращается в нуль.
2. Разложение по асимптотическому параметру. Рассмотрим более общую задачу, полученную введением произвольного асимптотического параметра e перед первой и второй производными от функции возмущения давления в центральном пласте по z, как в уравнениях, так и в граничных условиях задачи
|
|
(2.1) |
|
|
(2.2) |
|
|
(2.3) |
|
|
(2.4) |
|
|
(2.5) |
где ![]() .
.
Отметим, что решение исходной задачи может быть получено из решения параметризованной задачи при e = 1. Задача (2.1)—(2.5) является, таким образом, частным случаем более общей параметризованной, содержащей формальный параметр асимптотического разложения e.
Решение задачи (2.1)—(2.5) будем искать, представляя функцию давления Р каждой из областей асимптотической формулой по параметру e
|
|
(2.6) |
Подставив выражения (2.6) в (2.1)—(2.5) и сгруппировав слагаемые по степеням параметра разложения e, получим
|
|
(2.7) |
|
|
(2.8) |
|
|
(2.9) |
|
|
(2.10) |
|
|
(2.11) |
|
|
(2.12) |
Анализ задачи показывает, что сомножители при степенях e в (2.8) содержат соседние коэффициенты разложения и в этом смысле являются «зацепленными». Для решения соответствующего уравнения осуществлена процедура расцепления.
3. Постановка задачи в нулевом приближении. Формально устремим e к нулю в уравнении (2.8) получим ![]() . Результат интегрирования
. Результат интегрирования ![]() , с учетом граничных условий (2.9), (2.11) позволяет установить, что
, с учетом граничных условий (2.9), (2.11) позволяет установить, что ![]() . Таким образом, в нулевом приближении давление является функцией только от x и не зависит от z:
. Таким образом, в нулевом приближении давление является функцией только от x и не зависит от z: ![]() , т. е. одинаково в каждой точке любого сечения, параллельного оси z.
, т. е. одинаково в каждой точке любого сечения, параллельного оси z.
Далее, приравнивая к нулю коэффициенты при e в уравнении (2.8), получим
|
|
(3.1) |
Так как P(0)(x) не зависит от переменной z, вспомогательная функция E(x), составленная из слагаемых уравнения (3.1), содержащих P(0)
|
|
(3.2) |
также не зависит от z. Тогда (3.1) можно представить как
|
|
(3.3) |
Проинтегрировав последовательно, найдем выражения для первой производной от первого коэффициента P(1) по переменной z
|
|
(3.4) |
и первого коэффициента разложения в виде квадратного трехчлена
|
|
(3.5) |
с функциональными коэффициентами ![]() , подлежащими определению. Из граничных условий (2.11) при сомножителе
, подлежащими определению. Из граничных условий (2.11) при сомножителе ![]() в первой степени и (2.9) имеем
в первой степени и (2.9) имеем
|
|
(3.6) |
Отсюда следуют выражения для функциональных коэффициентов ![]() и
и ![]() через следы производных из внешних областей
через следы производных из внешних областей
|
|
(3.7) |
Подставив выражение (3.2) в (3.7), получим уравнение для определения нулевого приближения поля давления в пласте
|
|
(3.8) |
Окончательная постановка задачи в нулевом приближении включает также уравнения в покрывающих и подстилающих породах
|
|
(3.9) |
а также соответствующие граничные и начальные условия
|
|
(3.10) |
|
|
(3.11) |
Выражения (3.8)—(3.11) представляют краевую задачу для нулевого коэффициента разложения ![]() или нулевого приближения. Отметим, что эффективность используемого метода обусловлена тем, что вторая производная по вертикальной координате исходной задачи трансформировалась в след производной из внешней области — для нулевого коэффициента. Это обстоятельство в известном смысле перекликается с идеей интегральных преобразований, которые преобразуют производные в алгебраические выражения. Однако наиболее результативным в смысле построения конструктивных расчетных формул, как показано ниже, является комплексное использование обоих методов.
или нулевого приближения. Отметим, что эффективность используемого метода обусловлена тем, что вторая производная по вертикальной координате исходной задачи трансформировалась в след производной из внешней области — для нулевого коэффициента. Это обстоятельство в известном смысле перекликается с идеей интегральных преобразований, которые преобразуют производные в алгебраические выражения. Однако наиболее результативным в смысле построения конструктивных расчетных формул, как показано ниже, является комплексное использование обоих методов.
4. Осреднение исходной задачи. После интегрального осреднения задачи (1.1)—(1.5) по z в пределах от 0 до 1 по формуле
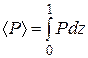
получим
|
|
(4.1) |
|
|
(4.2) |
|
|
(4.3) |
|
|
(4.4) |
Нетрудно заметить, что постановки задач (3.8)—(3.11) и (4.1)—(4.4) совпадают. Из единственности решения получим ![]() , то есть решения задач для нулевого коэффициента и осредненных значений температуры совпадают. Это определяет физический смысл нулевого коэффициента разложения или нулевого приближения и практическую важность его определения, поскольку поиском осредненных значений в подобного рода задачах чаще всего и ограничиваются.
, то есть решения задач для нулевого коэффициента и осредненных значений температуры совпадают. Это определяет физический смысл нулевого коэффициента разложения или нулевого приближения и практическую важность его определения, поскольку поиском осредненных значений в подобного рода задачах чаще всего и ограничиваются.
5. Решение в нулевом приближении. Решение уравнения (3.9) имеет вид
|
|
(5.1) |
Из условия ограниченности возмущения давления на бесконечности следует С2 = 0. Константу С1 найдем из условия (3.10) ![]() . Таким образом в нулевом приближении давление настилающего пласта выражается через давление проницаемого пласта соотношением
. Таким образом в нулевом приближении давление настилающего пласта выражается через давление проницаемого пласта соотношением
|
|
(5.2) |
Используя выражение (5.2), найдем производную P1(0) по вертикальной оси z 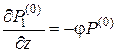 , подставив которую в (3.8), получим уравнение для нахождения Р(0)
, подставив которую в (3.8), получим уравнение для нахождения Р(0)
|
|
(5.3) |
Это уравнение можно представить в виде
|
|
(5.4) |
где ![]() .
.
Решение уравнение (5.4) выражается через функцию Бесселя нулевого порядка мнимого аргумента [1]
|
|
(5.5) |
Так как давление при ![]() конечная величина, то С4=0. Константу С3 найдем из условия (3.11) и известного предела
конечная величина, то С4=0. Константу С3 найдем из условия (3.11) и известного предела ![]()
|
|
(4.4) |
Решение задачи в нулевом приближении имеет вид
|
|
(5.6) |
|
|
(5.7) |
Из полученного решения следует, что в интервале пласта ![]() величина амплитуды давления
величина амплитуды давления ![]() не зависит от вертикальной координаты z, а определяется только радиальной коорднатой r. Это означает, что полученное нулевое приближение описывает в интервале пласта цилиндрическую волну, наиболее близкую к реальной, т. е. эквивалентную цилиндрическую волну давления.
не зависит от вертикальной координаты z, а определяется только радиальной коорднатой r. Это означает, что полученное нулевое приближение описывает в интервале пласта цилиндрическую волну, наиболее близкую к реальной, т. е. эквивалентную цилиндрическую волну давления.
Итак, применение «в среднем точной» модификации асимптотического метода к задаче о фильтрационно-волновом поле в неоднородной анизотропной среде позволяет найти простые аналитические выражения для нулевого коэффициента асимптотического разложения. Это открывает перспективы для решения других задач о фильтрационно-волновых полях в неоднородной пористой среде. Найденные решения описывают поля давления применительно к реальным условиям в акустическом каротаже, сейсморазведке и при интенсификации нефтеизвлечения.
Обозначения
с — скорость распространения фильтрационно-волновых возмущений, м/c;
k — проницаемость, м2;
m — пористость;
Р — давление, Па (атм.);
t — время;
![]() — скорость фильтрации, м/c;
— скорость фильтрации, м/c;
![]() — истинная скорость движения жидкости, м/c;
— истинная скорость движения жидкости, м/c;
x , z — линейные координаты;
a — коэффициент поглощения в пласте;
Β — коэффициент фазы;
![]() ,
, ![]() — коэффициент сжимаемости жидкости и среды скелета соответственно, Па-1;
— коэффициент сжимаемости жидкости и среды скелета соответственно, Па-1;
γ — коэффициент затухания, с-1;
![]() — коэффициент поглощения в окружающей среде;
— коэффициент поглощения в окружающей среде;
d — вспомогательная функция частоты;
e — параметр асимптотического разложения;
μ — вязкость, Па с;
ρ — плотность жидкости, кг/м3;
ρs — плотность материала скелета, кг/м3;
χ — коэффициент пъезопроводности, м2/с.
w — циклическая частота.
Индексы нижние: 0 — начальные значения параметров, 1 — номер среды, z, x — направление, d (dimension) — размерный.
Индексы верхние (в скобках) — порядковый номер коэффициента асимптотического разложения.
Обозначения математических символов — общепринятые.
Список литературы:
1.Кузнецов Д.С. Специальные функции. М.: Высшая школа, 1962. — 250 с.
2.Филиппов А.И., Ахметова О.В., Ковальский А.А., Повленкович Р.Ф. Фильтрационные волны в анизотропной среде // Естественные и математические науки в современном мире. — 2014. — № 14. — С. 57—63.
3.Филиппов А.И., Ахметова О.В., Заманова Г.Ф. Асимптотические представления упругих волновых полей в проницаемых пластах // Акустический журнал. — 2013. — Т. 59. — № 5. — C. 596—606
дипломов


 ,
,  ,
, 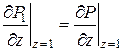 ,
,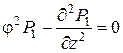 ,
,  ,
,  ,
, ,
, 
 ,
, 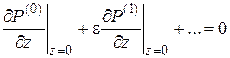 ,
,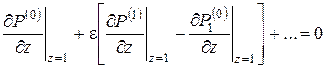 ,
,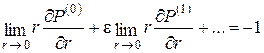 .
. .
.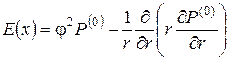
 .
.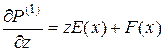

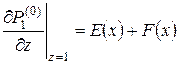 ,
,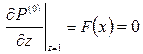 .
.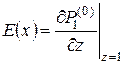 .
.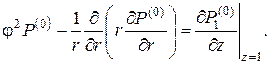
 ,
, .
.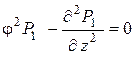 ,
, 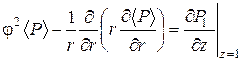 ,
, 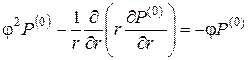 .
.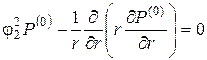 ,
,
Оставить комментарий