КРАЕВАЯ  ЗАДАЧА  ДЛЯ  ОДНОГО  ГИПЕРБОЛИЧЕСКОГО  УРАВНЕНИЯ  ВТОРОГО  РОДА

Вагапов  Винер  Зуфарович

канд.  физ.-мат.  наук,  доцент  Стерлитамакского  филиала  Башкирского  государственного  университета,  РФ,  Республика  Башкортостан,  г.  Стерлитамак

E-mail: 

BOUNDARY  VALUE  PROBLEM  FOR  ONE  HYPERBOLIC  EQUATION  OF  SECOND  KIND

Viner  Vagapov

candidate  of  Physical  and  Mathematical  Sciences,  associate  professor  of  Sterlitamak  branch  of  Bashkir  State  University,  Russian  Federation,  Republic  of  Bashkortostan  Sterlitamak

АННОТАЦИЯ

В  работе  для  одного  двуосесимметричного  уравнения  Гельмгольца  в  неограниченной  области  рассмотрена  краевая  задача  с  краевыми  условиями  на  бесконечно  удаленных  характеристиках.  Используя  решения  вспомогательных  задач  Коши,  решение  краевой  задачи  однозначно  редуцировано  к  системе  двух  интегральных  уравнений  Вольтера  с  функциями  Гаусса  в  ядрах.  Решение  задачи  построено  в  явном  виде.

ABSTRACT

There  is  considered  a  boundary  value  problem  with  boundary  conditions  and  infinitely  distant  characteristics  for  one  two-axis  symmetric  Helmholtz  equation  in  the  unbounded  domain.  Using  the  solutions  of  Cauchy  auxiliary  problems  the  solution  of  a  value  boundary  problem  is  clearly  reduced  to  two  integral  Volterra  equations’  system  with  Gaussian-type  functions  in  kernels.  Solution  of  the  problem  is  built  explicitly. 

Ключевые  слова:  уравнение  Гельмгольца;  краевая  задача.

Keywords:  Helmholtz's  equation;  regional  task. 

Рассмотрим  уравнение 

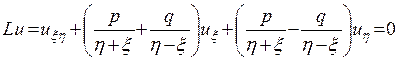  ,  (1)

где  ,  ,  на  множестве  ,  ,  .

Задача.  Найти  функцию    со  свойствами: 

1)  Lu≡0  в  D, 

2)    удовлетворяет  краевым  условиям:

  ,  (2)

  ,  (3)

3)    удовлетворяет  условию  сопряжения:

  .  (4)

Пользуясь  тем,  что  для  уравнения  (1)  известна  функция  Римана  [1],  вначале  в  областях    и    соответственно  методом  Римана  решим  следующие  задачи  Коши  с  данными  на  линии  :

,  ,

,  .

Решения  задач  Коши  имеют  соответственно  следующий  вид:

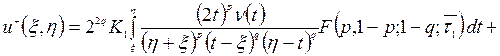
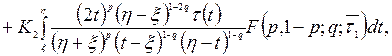    (5)

    (6)

где 

,  ,  ,  .

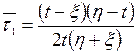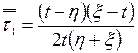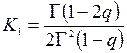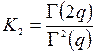Здесь    —  гипергеометрическая  функция  Гаусса  [2].

Исходя  из  них,  учитывая  краевые  условия  (2)  и  (3)  и  то,  что  ,  ,  придем  к  следующей  системе  интегральных  уравнений  относительно  функций    и  :

,

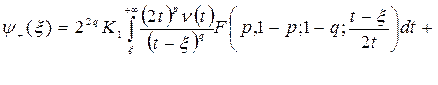
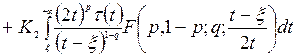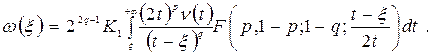
Преобразуем  полученную  систему  к  виду:

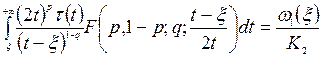,  (7)

,  (8)

где

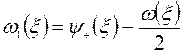  .  (9)

Рассмотрим  вначале  интегральное  уравнение  (7).  К  гипергеометрической  функции  Гаусса  в  ядре  применим  формулу  аналитического  продолжения  2.8(22)  [2].  Уравнение  (7)  примет  вид:

,

где  ,  .  Далее,  в  полученном  уравнении  выполним  замену  переменных: 

        .

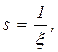
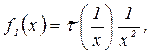
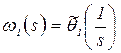Придем  к  уравнению

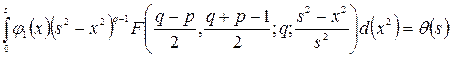  ,  (10)

где 

  .

Далее  воспользуемся  формулой  обращения,  полученной  профессором  В.Ф.  Волкодавовым  [3]  для  интегрального  уравнения  Вольтерра  с  гипергеометрической  функцией  Гаусса  в  ядре  вида 

,

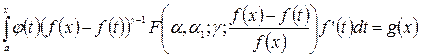в  котором  . 

В  результате  чего  получим  следующее  решение  уравнения  (10) 

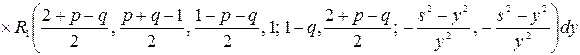  ,  (11)

где    —  гипергеометрическая  функция  двух  переменных,  введенная  в  рассмотрение  Волкодавовым  В.Ф.  [3].

Возвращаясь  в  (11)  к  прежним  переменным  и  обозначениям,  а  также  учитывая  соотношение  (9),  окончательно  имеем:

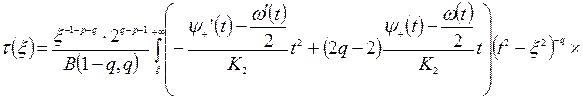
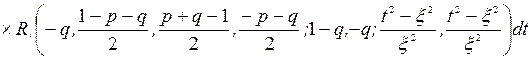    (12)

Чтобы  при  решении  уравнения  (10)  выполнялось  требование  ,  будем  считать,  что    при  ,  где    -  мало.

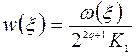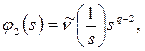
Перейдем  теперь  к  рассмотрению  интегрального  уравнения  (8).  Вводя  обозначения  ,  ,  выполним  в  нем  замену  переменных        .  В  результате  чего  уравнение  (8)  примет  вид 

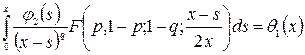  .  (13)

После  применения  к  гипергеометрической  функции  Гаусса  в  ядре  формулы  2.8(22)[2],  уравнение  (13)  становится  следующим:

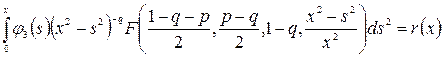  ,  (14)

где  ,  .

Для  получения  решения  уравнения  (14)  вновь  воспользуемся  результатом  профессора  В.Ф.  Волкодавова  [3].  Тогда  уравнение  (14)  имеет  решение

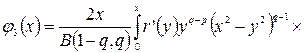
.  (15)

Для  выполнения  условия  ,  т.  е.  ,  будем  считать,  что    при  ,  где    -  мало. 

Возвращаясь  в  (15)  к  прежним  переменным  и  обозначениям,  окончательно  получим:

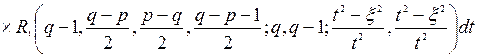  .  (16)

Теорема  Если  ,  ,  ,    при  ,    —  малы,  то  единственное  решение  задачи  1)-3)  определяется  формулами  (5)  и  (6),  где  функции    и    имеют  соответственно  вид  (12)  и  (16).

Список  литературы:

1.Волкодавов  В.Ф.,  Лернер  М.Е.,  Николаев  Н.Я.,  Носов  В.А.  Таблицы  некоторых  функций  Римана,  интегралов  и  рядов.  Куйбышев:  Куйбышев.  гос.  пед.  инс-т,  1982.  —  56  с.

2.Бейтмен  Г.,  Эрдейи  А.  Высшие  трансцендентные  функции.  Т.  1.  Гипергеометрическая  функция.  Функции  Лежандра.  М.:  Наука,  1973.  —  295  с.

3.Волкодавов  В.Ф.,  Николаев  Н.Я.  Интегральные  уравнения  Вольтерра  первого  рода  с  некоторыми  специальными  функциями  в  ядрах  и  их  приложения.  Самара:  Самарский  университет,  1992.  —  100  с.