ОБЛАСТЬ  УСТОЙЧИВОСТИ  НЕЙРОННОЙ  СЕТИ  С  ТОПОЛОГИЕЙ  В  ВИДЕ  ТОРА  ПРИ  РАЗРЫВЕ  НЕКОТОРЫХ  СВЯЗЕЙ

Речкалова  Лариса  Владимировна

магистрант,  факультет  информатики,  Челябинский  государственный  педагогический  университет,  РФ,  г.  Челябинск

Email:  rechkalovalv@cspu.ru

Кипнис  Михаил  Маркович

д-р  физ.-мат.  наук,  профессор,  кафедра  математики  и  методики  обучения  математике,  Челябинский  государственный  педагогический  университет,  РФ,  г.  Челябинск

Email:  '; // -->

THE  STABILITY  DOMAIN  OF  A  NEURAL  NETWORK  OF  TORUS  CONFIGURATIONS  WHEN  SOME  LINKS  ARE  BROKEN

Rechkalova  Larisa

graduate  student,  Dept.  of  Computer  Science,  Chelyabinsk  State  Pedagogical  University,  Russia  Chelyabinsk

Kipnis  Mikhail

professor,  PhD,  Department  of  Mathematics,  Chelyabinsk  State  Pedagogical  University,  Russia  Chelyabinsk

Работа  выполнена  при  поддержке  гранта  Министерства  образования  и  науки  1.1711.2011. 

АННОТАЦИЯ

Численными  экспериментами  получена  область  устойчивости  в  пространстве  параметров  дискретной  нейронной  сети  с  топологией  связей  в  виде  тора  и  проведено  сравнение  с  областями  устойчивости  нейронных  сетей  типа  цилиндр  и  плоское  поле,  которые  можно  получить  из  тора,  разорвав  некоторые  связи  между  нейронами.  Задача  сводится  к  проблеме  устойчивости  матричных  разностных  уравнений  высоких  порядков  с  запаздыванием. 

ABSTRACT

The  stability  domain  of  a  discrete  neural  network  are  obtained  by  numerical  experiments.  The  network  has  a  torus  architecture.  The  stability  domains  of  a  neural  networks  of  toroidal,  cylindrical,  similar  field  architectures  are  compared.  The  problem  is  reduced  to  the  matrix  delay  equations  of  higher  order. 

Ключевые  слова:  нейронные  сети;  разностные  матричные  уравнения;  устойчивость;  конфигурация  «тор».

Keywords:  neural  networks;  difference  matrix  equations;  stability;  torus.

Нейронная  сеть  это  система  соединённых  между  собой  и  влияющих  друг  на  друга  искусственных  нейронов.  Нейроны  периодически  посылают  сигналы  друг  другу.  Из-за  запаздываний  в  передаче  сигналов  в  нейронных  сетях  иногда  возникают  нежелательные  колебания,  это  называется  неустойчивостью.

Искусственные  нейронные  сети  с    нейронами  в  дискретном  линеаризованном  варианте  описываются  разностными  уравнениями  [3—5]

                                       .                        (1)

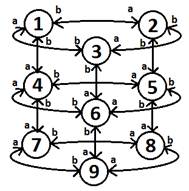
Мы  рассматриваем  нейронную  сеть  из  девяти  нейронов  с  архитектурой  связей  в  виде  тора  (Рисунок  1). 

Рисунок  1.  Нейронная  сеть  конфигурации  «тор»

Уравнение  (1)  для  этой  нейронной  сети  примет  вид

                                       ,                      (2)

где    единичная  матрица  размером  ,    коэффициент  демпфирования  собственных  колебаний  нейронов,  ,    матрица  взаимодействий  между  нейронами  в  сети  с  запаздыванием  ,    9-мерный  вектор  состояния  нейронной  сети  в  момент  .

Матрица  взаимодействий    имеет  вид

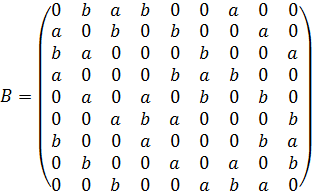                     ,                              (3)

где    сила  взаимодействия  между  нейронами,  действующая  по  часовой  стрелке,    сила  между  нейронами,  действующая  против  часовой  стрелки.

Устойчивость  нейронной  сети  это  стремление  к  нулю  векторов  состояний    при  ,  при  любых  начальных  условиях.

Характеристическое  уравнение  для  матричного  уравнения  (2)  таково:

                                                                   (4)

Уравнение  (4)  имеет  порядок  ,  где    —  запаздывание,    —  количество  нейронов  в  сети.  Нейронная  сеть  является  асимптотически  устойчивой,  если  корни  характеристического  уравнения    удовлетворяют  условию

                                                                                                     (5) 

При  фиксированном  значении  запаздывания    и  фиксированном  коэффициенте  демпфирования    с  помощью  программы  Mathcad  была  определена  область  устойчивости  в  плоскости  .

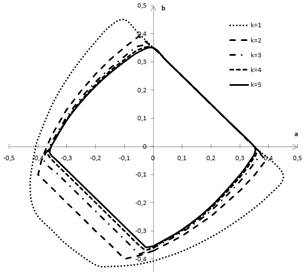
Рисунок  2.  Область  устойчивости  тора  в  плоскости    при 

В  процессе  проведения  численного  эксперимента  было  установлено,  что  коэффициент  запаздывания    влияет  на  размер  и  форму  области  устойчивости  для  нейронной  сети,  представленной  на  Рисунке  1  и  описанной  уравнением  (2)  с  матрицей  взаимодействий  (3).  Были  рассмотрены  запаздывания  на  1,  2,  3,  4  и  5  тактов  (Рисунок  2).  При  увеличении  коэффициента  запаздывания  ,  область  устойчивости  нейронной  сети  в  виде  тора  уменьшается.

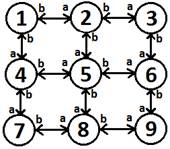
Рассмотрим  нейронную  сеть,  получаемую  в  результате  разрыва  некоторых  связей  между  нейронами  сети  с  топологией  в  виде  тора.  Топологию  этой  сети  назовем  «цилиндр»  (Рисунок  3).  В  работе  [1]  была  рассмотрена  нейронная  сеть  в  виде  цилиндра  из  шести  нейронов.

Рисунок  3.  Конфигурация  и  матрица  взаимодействий  нейронной  сети  в  виде  цилиндра  из  девяти  нейронов

Если  разорвать  некоторые  связи  в  цилиндре,  то  получим  нейронную  сеть  с  архитектурой  связей  в  виде  однородного  плоского  поля  (решетки)  [2].

Рисунок  4.  Конфигурация  и  матрица  взаимодействий  нейронной  сети  в  виде  решетки

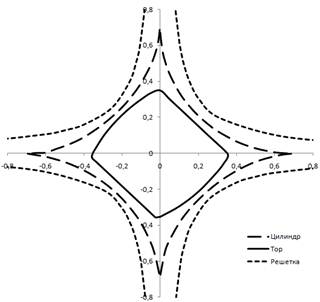
Рисунок  5.  Области  устойчивости  тора,  цилиндра  и  однородного  плоского  поля  в  плоскости    при    и 

Сравнивая  области  устойчивости  нейронных  сетей  разных  конфигураций  (Рисунок  5),  можно  сделать  вывод,  что  при  разрыве  некоторых  связей  конфигурация  становится  более  устойчивой  [5]  при  значениях  коэффициента  запаздывания  . 

Рисунок  6.  Области  устойчивости  тора,  цилиндра  и  однородного  плоского  поля  в  плоскости    при    и 

При    (Рисунок  6a)  область  устойчивости  однородного  поля  шире  области  устойчивости  цилиндра,  а  область  устойчивости  цилиндра  шире  области  устойчивости  тора,  но  есть  точки  [5],  в  которых  тор  устойчив,  а  цилиндр  и  решетка  неустойчивы  (область  1)  и  есть  точки,  в  которых  тор  и  цилиндр  устойчивы,  а  решетка  неустойчива  (область  2).

При 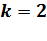   (Рисунок  6b)  область  устойчивости  решетки  в  целом  шире  области  устойчивости  цилиндра,  а  область  устойчивости  цилиндра  везде  шире  области  устойчивости  тора,  но  есть  точки,  в  которых  тор  неустойчив,  цилиндр  устойчив  и  решетка  неустойчива  (область  1)  и  есть  точки,  в  которых  тор  и  цилиндр  устойчивы,  а  решетка  неустойчива  (область  2)  .

Список  литературы:

1.Иванов  С.А.,  Козлова  С.А.,  Невзорова  Е.Н.  Устойчивость  рекурсивных  нейронных  сетей  цилиндрической  архитектуры  с  запаздывающими  взаимодействиями  //  «Инновации  в  науке»:  материалы  XVI  международной  заочной  научно-практической  конференции.  Новосибирск:  Изд.  «СибАК»,  —  2013.  —  Ч.  1.  —  С.  7—11.

2.Иванов  С.А.,  Пархоменко  А.А.  Устойчивость  плоского  однородного  нейронного  поля  //  «Инновации  в  науке»:  материалы  XVI  международной  заочной  научно-практической  конференции.  Новосибирск:  Изд.  «СибАК»,  —  2013.  —  Ч.  1.  —  С.  11—16.

3.Ivanov  S.A.,  Kipnis  M.M.  Stability  analysis  of  discrete-time  neural  networks  with  delayed  interactions:  torus,  ring,  grid,  line.  //  International  Journal  of  Pure  and  Applied  Math.  (2012)  V.  78(5).  —  P.  691—709.

4.Khokhlova  T.N.,  Kipnis  M.M.  Numerical  and  qualitative  stability  analysis  of  ring  and  linear  neural  networks  with  a  large  number  of  neurons  //  International  Journal  of  Pure  and  Applied  Math.  (2012)  V.  76(3).  —  P.  403—419.

5.Khokhlova  T.N.,  Kipnis  M.M.  The  breaking  of  a  delayed  ring  neural  network  contributes  to  stability:  The  rule  and  exceptions  //  Neural  Networks  (2013)  V.  48.  —  P.  148—152.