Статья опубликована в рамках: XXVII Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 02 декабря 2013 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ВЛИЯНИЕ ВОДНОГО БАРЬЕРА НА ЭФФЕКТИВНОСТЬ ТУШЕНИЯ ЛЕСНОГО ПОЖАРА
Романова Наталья Алексеевна
ассистент Нижегородского государственного технического университета им. Р.Е. Алексеева, РФ, г. Нижний Новгород
Маслеников Дмитрий Александрович
ассистент, канд. физ.-мат. наук Нижегородского государственного технического университета им. Р.Е. Алексеева, РФ, г. Нижний Новгород
E-mail: dmitrymaslennikov@rambler.ru
Белоцерковская Ирина Ефимовна
ассистент Нижегородского государственного технического университета им. Р.Е. Алексеева, РФ, г. Нижний Новгород
E-mail: miran_kaspir@mail.ru
Катаева Лилия Юрьевна
д-р физ.-мат. наук, профессор Нижегородского государственного технического университета им. Р.Е. Алексеева, РФ, г. Нижний Новгород, профессор Нижегородского Филиала Московского государственного университета путей сообщения, РФ, г. Нижний Новгород
E-mail:
INFLUENCE OF THE WATER BARRIER ON THE EFFICIENCY OF FOREST FIRE EXTINGUISHING
Nataly Romanova
assistant, Nizhny Novgorod State Technical University. R.E. Alekseev, Russia Nizhny Novgorod
Dmitriy Maslennikov
assistant, PhD. Physics and Mathematics Nizhny Novgorod State Technical University. R.E. Alekseev, Russia Nizhny Novgorod
Irina Belocerkovskay
assistant, Nizhny Novgorod State Technical University. R.E. Alekseev, Russia Nizhny Novgorod
Liliy Kataeva
Doctor of Physics and Mathematics, Professor, of Nizhny Novgorod State Technical University. R.E. Alekseev, Russia Nizhny Novgorod
АННОТАЦИЯ
Данная работа посвящена моделированию тушения пожара на основе математической модели. Водный барьер может быть образован путём смачивания лесных материалов или как аналог пожарной помпы (пожарный центробежный насос). В отличие от влаги, находящейся в древесине, у свободной воды существует температура кипения, которая считалась постоянной в данной работе (373 К). Показано влияние рельефа на количество воды в водном барьере, требуемой для его тушения. Так как обтекание оврага способствует растягивания фронта, то его тушение там неэффективно.
ABSTRACT
This work is devoted to the modeling of fire extinguishing on the basis of mathematical model. The moisture barrier can be formed by wetting forest materials or as an analogue fire pump (fire-fighting centrifugal pump). Unlike the moisture contained in the wood, there is free water boiling point, which was considered to be constant in this work (373 K). Shows the influence of the relief on the amount of water in a water barrier required for extinguishing it. As runaround ravine helps to stretch the front, his extinguishing there inefficient.
Ключевые слова: численное моделирование; лесные пожары; тушение пожаров.
Keywords: numerical simulation; forest fires; extinguishing.
Одним из основных средств тушения лесных пожаров является, как правило, вода. Её неэффективное использование является ключевым недостатками существующих подходов к тушению пожаров. Наличие рельефа приводит к возникновению эффектов обтекания, которые в свою очередь существенно влияют на динамику пожара [8]. В данной работе предполагается использование математической модели взаимодействия воды с пожаром, позволяющая учитывать гидродинамику пожара.
В математической модели лесных пожаров, рассмотренных в работах Катаевой [3], [4] и Масленникова [5], [6], скорость химико-физических процессов, в том числе испарения воды, вычисляется по закону Аррениуса. В отличие от влаги, находящейся в древесине, у свободной воды существует температура кипения, которую можно приблизительно считать постоянной с учётом величины перепада давления в области горения. В настоящей статье тушением пожара называется процесс взаимодействия свободной воды с фронтом пожара, которая поглощает энергию пожара за счёт испарения и, вытесняя кислород, что препятствует распространению пожара.
Для моделирования свободной воды в математическую постановку [2], [7] вводится соответствующая ей новая фаза и соотношения, моделирующие её поведение [1] (1—4):
![]() (1)
(1)
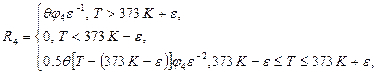 (2)
(2)
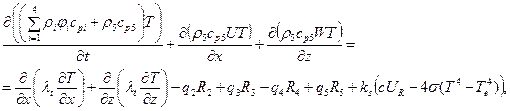 (3)
(3)
![]() . (4)
. (4)
Уравнение (2) с одной стороны моделирует резкое возникновение реакции кипения при достижении заданной температуры, с другой стороны зависимость скорости реакции от температуры носит непрерывный характер. В уравнении (3) и (4) вносится тепловой эффект реакции кипения и переход массы испарённой воды в массу водяного пара.
В данной статье рассматривается моделирование тушения пожара с помощью расположенного на пути его следования водного барьера. Барьер расположен на расстоянии 20 м от левого края расчётной области, его ширина составляет 0,4 м, по вертикали барьер занимает всю высоту леса. В начальный момент вода в барьере распределена равномерно. Начальные условия объемной доли воды в барьере имеют вид:
![]() , (5)
, (5)
Для расчёта количества воды, требуемой для создания водного барьера можно использовать соотношение:
![]() (6)
(6)
где: ![]() — достаточно малая положительная константа, К;
— достаточно малая положительная константа, К;
![]() ;
;
![]() — объёмная доля свободной воды;
— объёмная доля свободной воды;
![]() — отношение массы воды к массе лесных горючих материалов в барьере;
— отношение массы воды к массе лесных горючих материалов в барьере;
![]() — плотность воды, кг/м3;
— плотность воды, кг/м3;
T — температура среды, K;
![]() — плотность, объёмная доля и удельная теплоёмкость i-й фазы, кг/м3, безразмерная величина, Дж/(кг·К);
— плотность, объёмная доля и удельная теплоёмкость i-й фазы, кг/м3, безразмерная величина, Дж/(кг·К);
U, W — горизонтальная и вертикальная компоненты скорости газовой фазы, м/с;
![]() — теплопроводность газовой фазы, Вт/(м·K);
— теплопроводность газовой фазы, Вт/(м·K);
![]() — удельный тепловой эффект и массовая скорость химико-физических процессов соответственно (i=2 — испарение влаги, находящейся в лесных горючих материалах, i=3 — горение конденсированных продуктов пиролиза, i=4 — кипение свободной воды, i=5 — горение летучих продуктов пиролиза), Дж/кг, кг/с;
— удельный тепловой эффект и массовая скорость химико-физических процессов соответственно (i=2 — испарение влаги, находящейся в лесных горючих материалах, i=3 — горение конденсированных продуктов пиролиза, i=4 — кипение свободной воды, i=5 — горение летучих продуктов пиролиза), Дж/кг, кг/с;
![]() — спектральный коэффициент поглощения,
— спектральный коэффициент поглощения,
с — скорость света, м/с;
![]() — плотность потока излучения, кг·(м/с2);
— плотность потока излучения, кг·(м/с2);
![]() — постоянная Стефана-Больцмана, кг·с-3·К-4;
— постоянная Стефана-Больцмана, кг·с-3·К-4;
![]() — температура окружающей среды, К;
— температура окружающей среды, К;
![]() — масса воды, необходимая для создания барьера, кг;
— масса воды, необходимая для создания барьера, кг;
![]() — объём водного барьера, м3;
— объём водного барьера, м3;
![]() — доля потраченной воды, оставшейся в барьере.
— доля потраченной воды, оставшейся в барьере.
При проведении практических вычислений, предполагается, что в каждой ячейке, имеющей температуру выше 373 К и ненулевую долю свободной воды, имеет место кипение. Его скорость определяется минимумом между количеством свободной воды, которая есть в ячейке и количеством, для кипения которой достаточно энергии. Очаг пожара был задан на расстоянии 12 м от водного барьера.
Согласно проведённым расчётам (рис. 1—6), пожар может преодолеть барьер или погаснуть в зависимости от доли воды в барьере. Для выполнения расчётов были выбраны три модельные конфигурации рельефа: холм, равнина и овраг.
Для определения критического значения доли воды, необходимой для предотвращения дальнейшего распространения пожара, был использован метод дихотомии. При проведении расчётов, предполагается, что существует критическое значение ![]() , такое, что пожар преодолевает барьер при любом значении
, такое, что пожар преодолевает барьер при любом значении ![]() и гаснет при
и гаснет при ![]() .
. ![]() означает, что при сложившихся условиях пожар гаснет даже в отсутствии барьера. Пожар считается потушен при выполнении двух ключевых критериев: если максимальная температура в пологе леса упала ниже 700 К; если доля сухого органического вещества на расстоянии 4 м от границы составляет менее
означает, что при сложившихся условиях пожар гаснет даже в отсутствии барьера. Пожар считается потушен при выполнении двух ключевых критериев: если максимальная температура в пологе леса упала ниже 700 К; если доля сухого органического вещества на расстоянии 4 м от границы составляет менее ![]() .
.
На рис. 1—3 показана динамика пожара. Тонкая сплошная, тонкая штриховая и жирная сплошная линии соответствуют температурам 1500 К, 1000 К, 500 К. Стрелки показывают поле скоростей. Водный барьер отображён в виде синей области, толщина которой соответствует распределению доли воды, оставшейся в барьере по высоте.
На рис.1 представлена динамика пожара на различные моменты времени при распространении пожара через трапециевидный холм. Отношение массы воды в барьере к массе сухого органического вещества ![]() =1,23 и 1,24 соответственно. Из рис. 1 (слева) видно, что отличия в динамике пожара незначительны на момент времени 6,8 сек. В связи с тем, что пламя наклонено вперёд, испарение воды в барьере происходит преимущественно в его верхней части. Дальнейшее распространение характеризуется резким снижением температуры в верхней части полога леса за счёт расхода энергии на испарение барьера. Незначительные различия в количестве воды в барьере оказывают существенное влияние на динамику пожара после испарения барьера: так, на рис. 1 слева на момент 11,2 сек видно, как вновь формируется фронт пожара, тогда как на рис. 1 справа можно видеть отрыв горячих газовых масс и постепенное затухание пожара. Заметим, что водный барьер в обоих случаях полностью испаряется.
=1,23 и 1,24 соответственно. Из рис. 1 (слева) видно, что отличия в динамике пожара незначительны на момент времени 6,8 сек. В связи с тем, что пламя наклонено вперёд, испарение воды в барьере происходит преимущественно в его верхней части. Дальнейшее распространение характеризуется резким снижением температуры в верхней части полога леса за счёт расхода энергии на испарение барьера. Незначительные различия в количестве воды в барьере оказывают существенное влияние на динамику пожара после испарения барьера: так, на рис. 1 слева на момент 11,2 сек видно, как вновь формируется фронт пожара, тогда как на рис. 1 справа можно видеть отрыв горячих газовых масс и постепенное затухание пожара. Заметим, что водный барьер в обоих случаях полностью испаряется.
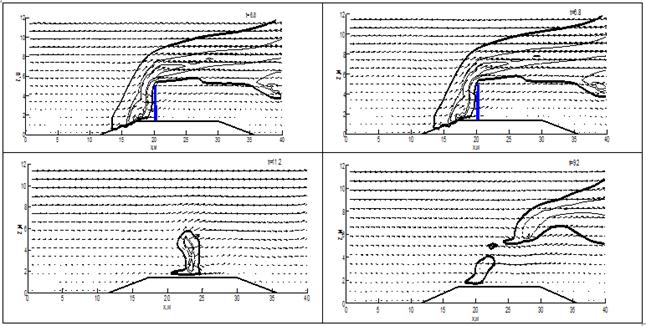
Рисунок 1. Динамика лесного пожара при распространении через водный барьер по холму; отношение массы воды в барьере к массе сухого органического вещества ![]() =1,23(слева),
=1,23(слева), ![]() =1,24(справа)
=1,24(справа)
На рис. 2 представлена динамика пожара на различные моменты времени при распространении пожара через равнину. Отношение массы воды в барьере к массе сухого органического вещества ![]() =0,78 и 0,79 соответственно.
=0,78 и 0,79 соответственно.
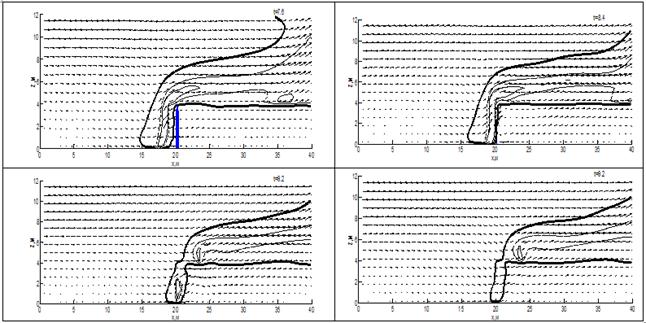
Рисунок 2. Динамика лесного пожара при распространении через водный барьер по равнине; отношение массы воды в барьере к массе сухого органического вещества ![]() =0,78(слева),
=0,78(слева), ![]() =0,79(справа)
=0,79(справа)
Ещё до столкновения с водным барьером ядра пожара, вода в барьере начинается испаряться. Несмотря на незначительность различия количества воды в барьере в расчётах, результаты которых показаны на рис. 2, можно видеть некоторые отличия в полях скоростей перед барьером. Следует отметить, что на рис. 2 (справа) за промежуток времени от 8,4 до 9,2 сек происходит активное охлаждение фронта пожара, даже, несмотря на практически полное испарение водного барьера. Этот эффект обуславливается с одной стороны тем, что барьер препятствовал распространению тепла и как следствие пиролизу и сушке лесных горючих материалов, вследствие чего энергия пожара была израсходована на сушку.
На рис. 3 представлена динамика пожара на различные моменты времени при распространении пожара через овраг. Отношение массы воды в барьере к массе сухого органического вещества ![]() =3,48 и 3,49 соответственно.
=3,48 и 3,49 соответственно.
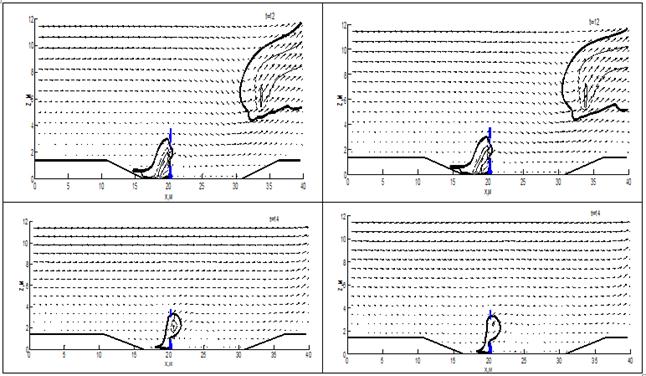
Рисунок 3. Динамика лесного пожара при распространении через водный барьер по оврагу; отношение массы воды в барьере к массе сухого органического вещества ![]() =3,48(слева),
=3,48(слева), ![]() (справа)
(справа)
На рис. 3 ввиду увеличения скорости газовой фазы с ростом высоты, пожар пробивает барьер в середине, при этом в нижней и верхней части барьера ещё остаётся запас воды, и они частично сдерживают пожар, продолжаю испаряться. В момент 14 сек, ядро пожара преодолевает барьер. В зависимости от массы воды в барьере пожар либо затухает, либо разгорается. Низкая скорость ветра в области ядра пожара препятствует интенсивному оттоку энергии, что даёт возможность пожару разгореться. Следует отметить, что разработанный алгоритм определяет критическое соотношение воды в барьере, но не отвечает на вопрос о возможности удерживания лесными материалами такого количества воды.
В данной статье продемонстрирован подход к моделированию тушения пожара с помощью свободной воды на основе математической модели, учитывающей гидродинамику. Поле скоростей определяет угол наклона факела пламени, который свою очередь влияет на эффективность водного барьера (с увеличением наклона факела пламени растёт требуемое для тушения количество воды).
Список литературы:
1.Белоцерковская И.Е., Масленников Д.А., Катаева Л.Ю., Лощилов С.А. Влияние водного барьера на динамику ландшафтных лесных пожаров // Естественные и технические науки, — 2013, — № 3, — с. 26—31.
2.Катаева Л.Ю. Анализ динамических процессов аварийных ситуаций природного и техногенного характера: Дис. … д-ра. физ.-мат. наук. Нижний Новгород, 2009.
3.Катаева Л.Ю. О методе Гира численного моделирования динамических систем, описываемых жесткими обыкновенными дифференциальными уравнениями/Л.Ю. Катаева, В.Б. Карпухин // Наука и техника транспорта. М.:РГОТУПС, — 2008, — № 1. — С. 57—66
4.Катаева Л.Ю., Белоцерковская И.Е., Масленников Д.А., Куркин А.А. Сравнение аналитического и численного решения математической модели низового пожара с учетом влияния угла наклона подстилающей поверхности // Пожаровзрывобезопасность. — 2010. — Т. 19, — № 11. — С. 25—31.
5.Масленников Д.А. Особенности математического моделирования распространения лучистого теплового потока от очага горения при лесных пожарах на неоднородном рельефе: Дис. … канд. физ.-мат. наук. Нижний Новгород, 2012.
6.Масленников Д.А., Катаева Л.Ю., Белоцерковская И.Е. Численное моделирование динамики пожара с учетом рельефа местности и внешнего поля скоростей // Пожаровзрывобезопасность. М.: Пожнаука, — 2012. — Т. 21, — № 12. — C. 13.
7.Масленников Д.А. Влияние холмов на динамику лесного пожара / Д.А. Масленников, Л.Ю. Катаева, Н.В. Галина // Успехи современного естествознания: материалы конференции / Пенза — 2012. — № 6 — С. 189—189.
8.Романов A.B., Катаева Л.Ю. Метод Патанкара и возможности его оптимизации// Наука и техника транспорта, № 3, 2008. М.:РГОТУПС.
дипломов


Оставить комментарий