Статья опубликована в рамках: XXIV Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 09 сентября 2013 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ОБ ОДНОЙ МНОГОТОЧЕЧНОЙ КРАЕВОЙ ЗАДАЧЕ
Митрохин Сергей Иванович
канд. физ.-мат. наук, доцент, старший научный сотрудник НИВЦ МГУ им. М.В. Ломоносова, г. Москва
ABOUT ONE MULTIPOINT BOUNDARY VALUE PROBLEM
Sergey Mitrohin
candidate of Physical and Mathematical Sciences, associate professor, senior research scientist of Research Computing Center of M.V. Lomonosov Moscow State University, Moscow
АННОТАЦИЯ
В статье изучена многоточечная краевая задача для дифференциального оператора нечётного порядка, которая возникает при исследовании колебаний балок и мостов. Потенциал предполагается суммируемой функцией на рассматриваемом отрезке. Впервые изучена асимптотика решений уравнения с суммируемым коэффициентом, выведено уравнение на собственные значения этой задачи. Методами спектральной теории дифференциальных операторов найдена асимптотика собственных значений рассматриваемой краевой задачи.
ABSTRACT
The article studies a multipoint boundary value problem for a differential operator of odd order, which appears during an investigation of a variance of beams and bridges. The potential is hypothesized by a summable function at a given interval. An asymptotics of solutions of an equation with a summable coefficient was examined for the first time; an equation on eigenvalues of this problem was established. Using methods of spectral theory of differential operators there was found the asymptotics of eigenvalues of the boundary value problem in question.
Ключевые слова: многоточечная краевая задача; дифференциальный оператор; суммируемый потенциал; асимптотика решений; асимптотика собственных значений.
Keywords: multipoint boundary value problem; differential operator; summable potential; asymptotics of solutions; asymptotics of eigenvalues.
Изучим следующую краевую задачу:
![]() (1)
(1)
с граничными условиями
![]() (2)
(2)
потенциал ![]() предполагается суммируемой функцией на отрезке
предполагается суммируемой функцией на отрезке ![]() .
.
Впервые такой тип граничных условий (для дифференциального оператора четвёртого порядка) был изучен Ю. Белабасси в работе [1].
Случай суммируемого потенциала (для дифференциального оператора второго порядка) впервые изучен в работах [2], [3]. В работах [4], [5], [6] автором изучены спектральные свойства дифференциальных и функционально-дифференциальных операторов четвёртого и шестого порядков с суммируемыми коэффициентами. Методами работ [7], [8], [9] доказывается следующее утверждение.
Теорема 1. Общее решение дифференциального уравнения (1) имеет следующий вид:
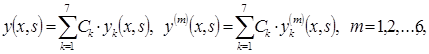 (3)
(3)
где: ![]() — произвольные постоянные, причём для фундаментальной системы решений
— произвольные постоянные, причём для фундаментальной системы решений ![]() справедливы следующие асимптотические разложения при
справедливы следующие асимптотические разложения при ![]() :
:
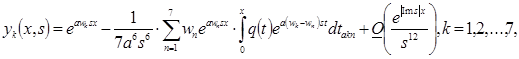 (4)
(4)
где: ![]() — различные корни 7-ой степени из единицы,
— различные корни 7-ой степени из единицы,
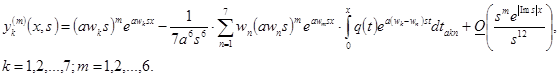 (5)
(5)
Перенумеруем числа ![]() следующим образом:
следующим образом:
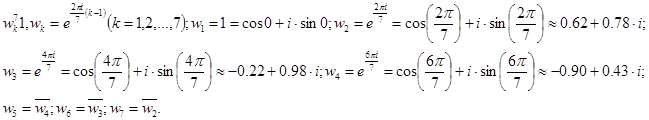
Подставляя формулы (3) в граничные условия (2), имеем:
![]() (6)
(6)
Система (6) — однородная система из семи уравнений с семью неизвестными. Из метода Крамера следует, что такие системы имеют ненулевые решения ![]() только в том случае, когда их определитель равен нулю. Поэтому верна следующая теорема.
только в том случае, когда их определитель равен нулю. Поэтому верна следующая теорема.
Теорема 2. Уравнение на собственные значения краевой задачи (1)—(2) имеет следующий вид:
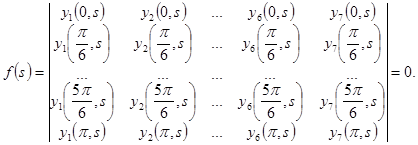 (7)
(7)
Подставляя формулы (4)—(5) в уравнение (7), получаем:
 (8)
(8)
где введены обозначения:
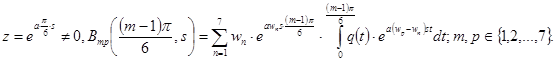 (9)
(9)
Раскладывая определитель ![]() из (8)—(9) по столбцам на сумму определителей, приходим к выводу, что
из (8)—(9) по столбцам на сумму определителей, приходим к выводу, что
![]() (10)
(10)
 (11)
(11)
Основное приближение уравнения (10) (при ![]() ) имеет вид
) имеет вид
![]() . (12)
. (12)
Вычисляя определитель ![]() из (11)—(12), имеем:
из (11)—(12), имеем:
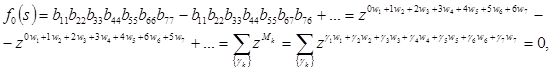 (13)
(13)
![]() при
при ![]() .
.
Всего в уравнении (13) ![]() слагаемых. Из общей теории нахождения асимптотики корней (при
слагаемых. Из общей теории нахождения асимптотики корней (при ![]() ) уравнения вида (10)—(13) (см. [10, глава 12]) следует, что необходимо изучить так называемую индикаторную диаграмму этих уравнений, т.е. выпуклую оболочку показателей экспонент, входящих в уравнение (12)—(13). В силу обозначений (5) имеем:
) уравнения вида (10)—(13) (см. [10, глава 12]) следует, что необходимо изучить так называемую индикаторную диаграмму этих уравнений, т.е. выпуклую оболочку показателей экспонент, входящих в уравнение (12)—(13). В силу обозначений (5) имеем:
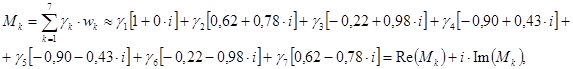 (14)
(14)
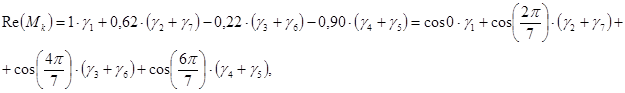 (15)
(15)
 (16)
(16)
Из формул (14)—(16) видно, что ![]() достигается в случае, когда
достигается в случае, когда
![]() при этом (17)
при этом (17)
![]()
В формуле (17) возможны 8 различных случаев выбора точек ![]() , поэтому одной из сторон индикаторной диаграммы уравнений (8)—(9), (10)—(11) или (12)—(13) является вертикальный отрезок
, поэтому одной из сторон индикаторной диаграммы уравнений (8)—(9), (10)—(11) или (12)—(13) является вертикальный отрезок ![]() , при этом координаты точек равны
, при этом координаты точек равны ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Это означает, что одна из серий собственных значений краевой задачи (1)—(2) находится в секторе малого раствора, биссектриса которого перпендикулярна отрезку
. Это означает, что одна из серий собственных значений краевой задачи (1)—(2) находится в секторе малого раствора, биссектриса которого перпендикулярна отрезку ![]() и проходит через середину этого отрезка, т.е. через точку
и проходит через середину этого отрезка, т.е. через точку ![]() .
.
Точки ![]() соответствуют следующим перестановкам чисел
соответствуют следующим перестановкам чисел ![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , знаки этих перестановок равны
, знаки этих перестановок равны ![]() .
.
Поэтому из представления (13) с учётом формул (11), (10) и (12) следует справедливость следующего утверждения.
Теорема 3. В секторе![]() уравнение на собственные значения краевой задачи (1)—(2) имеет следующий вид:
уравнение на собственные значения краевой задачи (1)—(2) имеет следующий вид:
 (19)
(19)
Проведя необходимые преобразования, уравнение (19) можно привести к следующему виду:
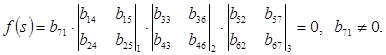 (20)
(20)
Из (20) видно, что серия собственных значений, соответствующая сектору ![]() , распадается на три отдельные подсерии, например,
, распадается на три отдельные подсерии, например,
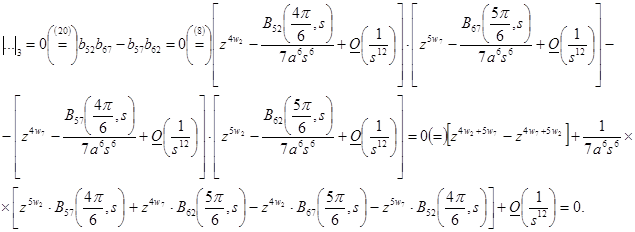 (21)
(21)
Изучая уравнение на (21), получим одну из трёх подсерий первой серии собственных значений краевой задачи (1)—(2).
Список литературы:
1.Белабасси Ю. Регуляризованный след многоточечной задачи // Вестник Московского университета. Серия: математика. — 1981. — № 2. — С. 35—41.
2.Беллман Р., Кук К. Л. Дифференциально-разностные уравнения. М.: Мир, 1967. — 548 с.
3.Винокуров В.А., Садовничий В.А. Асимптотика любого порядка собственных значений и собственных функций краевой задачи Штурма- Лиувилля на отрезке с суммируемым потенциалом // Дифференциальные уравнения. — 1998. — Т. 34, — № 10. — С. 1423—1426.
4.Винокуров В.А., Садовничий В.А. Асимптотика любого порядка собственных значений и собственных функций краевой задачи Штурма-Лиувилля на отрезке с суммируемым потенциалом // Известия РАН. Серия: матем. — 2000. — Т. 64, — № 4. — С. 47—108.
5.Митрохин С.И. Асимптотика собственных значений дифференциального оператора четвёртого порядка с суммируемыми коэффициентами // Вестник Московского университета. Сер.1, математика, механика. — 2009. — № 3. — С. 14—17.
6.Митрохин С.И. Спектральные свойства краевых задач для функционально-дифференциальных уравнений с интегрируемыми коэффициентами // Дифференциальные уравнения, — 2010. — Т. 46, — № 8. — С. 1085—1093.
7.Митрохин С.И. Асимптотика собственных значений дифференциального оператора десятого порядка с суммируемым потенциалом // Успехи современного естествознания. — 2010. — № 3. — С. 146—149.
8.Митрохин С.И. О спектральных свойствах дифференциального оператора с суммируемым потенциалом и гладкой весовой функцией. // Вестник СамГУ — естественнонаучная серия. — 2009. — № 8/1(67). — С. 172—187.
9.Митрохин С.И. О некоторых спектральных свойствах дифференциальных операторов второго порядка с разрывной весовой функцией // Доклады РАН. — 1997. — Т. 356, — № 1. — С. 13—15.
10.Митрохин С.И. Асимптотика решений дифференциального уравнения третьего порядка с суммируемыми коэффициентами // М.: МГСУ, 2010. — Сборник научных трудов. Выпуск 12. — С. 38—48.
дипломов


Оставить комментарий