Статья опубликована в рамках: XXIII Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 12 августа 2013 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ПОЛУЧЕНИЕ ТЕОРЕТИЧЕСКИХ ПАРАМЕТРОВ УРАВНЕНИЯ МНОЖЕСТВЕННОЙ РЕГРЕССИИ С ПОМОЩЬЮ МИНИМИЗАЦИИ ФУНКЦИОНАЛА ОШИБКИ
Орлов Николай Николаевич
канд. физ.-мат. наук, доцент, Институт коммерции и права, зав. кафедрой информатики и математики, г. Москва
Орлова Елена Юрьевна
канд. техн. наук, доцент, Международный университет природы, общества и человека «Дубна», зав. заочным отделением филиала «Котельники», г. Дубна
E-mail: orlova.elena.urjevna@mail.ru
OBTAINING OF THE THEORETICAL PARAMETERS OF MULTIPLE REGRESSION EQUATION USING THE MINIMIZATION OF THE ERROR FUNCTION
Nikolai Orlov
phd of Physical and Mathematical Sciences, Professor, Institute of Commerce and Law, Head of Department of Computer Science and Mathematics, Moscow
Elena Orlova
phd of Science, Associate Professor, International University of Nature, Society and Man "Dubna", Head of the department of distance learning branch "Kotelniki", Dubna
АННОТАЦИЯ
Работа посвящена корреляционно-регрессионному анализу. Получены теоретические параметры множественной (в общем случае нелинейной) регрессии и коэффициент детерминации путем минимизации функционала ошибки. Приведены примеры нахождения параметров и коэффициентов детерминации для случаев парной линейной и квадратической регрессий, а также множественной линейной регрессии трех случайных величин.
ABSTRACT
The work is dedicated to the correlation-regression analysis. The theoretical parameters of multiple (generally non-linear) regression and determination coefficient by minimization of the error function are received. Examples of finding the parameters for the cases of pair-wise linear and square regressions, as well as the multiple linear regression of three random variables are given.
Ключевые слова: множественная регрессия; ошибка аппроксимации; минимум функционала; коэффициенты уравнения; коэффициент детерминации, анализ коррелируемости величин.
Keywords: multiple regression; approximation error; minimum of the functional; the coefficients of the equation; the determination coefficient; analysis of the relationship values.
Введение
Для нахождения эмпирических коэффициентов в уравнении регрессии используется метод наименьших квадратов (МНК) [1]. В данной работе с помощью минимизации функционала определенного вида получены формулы теоретических параметров уравнения множественной регрессии (достаточно произвольного вида) и коэффициента детерминации. Из полученных соотношений, используя известные формулы математической статистики, можно записать эмпирические коэффициенты уравнения регрессии и детерминации.
1. Функционал ошибки и его минимум
Пусть имеются непрерывные случайные величины (СВ) ![]() и
и ![]() с функцией плотности распределения вероятностей
с функцией плотности распределения вероятностей ![]() . Требуется найти такую линейную относительно коэффициентов
. Требуется найти такую линейную относительно коэффициентов ![]() аппроксимацию (1), в которой СВ
аппроксимацию (1), в которой СВ ![]() была бы наименьшей в «вероятностном» смысле:
была бы наименьшей в «вероятностном» смысле:
![]() (1)
(1)
Здесь 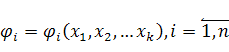 — некоторое множество линейно независимых функций от СВ
— некоторое множество линейно независимых функций от СВ ![]()
![]() — некоторые параметры (коэффициенты), подлежащие определению.
— некоторые параметры (коэффициенты), подлежащие определению.
Будем искать значения 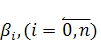 путем минимизации функционала, учитывающего не только ошибку
путем минимизации функционала, учитывающего не только ошибку ![]() , но и вероятность
, но и вероятность
![]() попадания в область пространства
попадания в область пространства ![]() :
:
|
|
(2) |
Где
|
|
(3) |
и интегрирование ведется по всему «объему» ![]() .
.
Так как функции ![]() и
и ![]() для любых значений
для любых значений 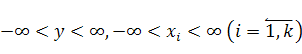 , то функционал
, то функционал ![]() имеет минимум, который находится из условий:
имеет минимум, который находится из условий:
|
|
(4) |
2. Получение коэффициентов множественной регрессии
Найдем частные производные от рассматриваемого функционала и приравняем их к нулю:
|
|
|
|
5) |
|
|
|
|
|
6) |
Здесь ![]()
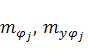 и
и ![]() — математические ожидания от функций
— математические ожидания от функций 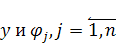 .
.
Из условий (4), получим систему линейных уравнений для определения коэффициентов ![]() :
:
|
|
(7) |
Выразим из 1-ого уравнения системы (7) параметр ![]() через остальные коэффициенты
через остальные коэффициенты 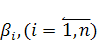 :
:
|
|
(8) |
и подставим его в оставшиеся уравнения:
|
|
|
или
|
|
(9) |
Здесь ![]() — ковариации функций
— ковариации функций ![]() и
и 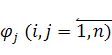 СВ
СВ ![]() :
:
|
|
|
|
|
(10) |
![]() — ковариации функций
— ковариации функций ![]() и
и  СВ
СВ ![]() , соответственно.
, соответственно.
Представим систему уравнений (9) в матричном виде:
|
|
(11) |
Где
|
|
(12) |
Матрица ![]() — симметричная (
— симметричная (![]() ), так как
), так как  .
.
Для невырожденной матрицы ![]() получим коэффициенты уравнения регрессии:
получим коэффициенты уравнения регрессии:
|
|
(13) |
Здесь ![]() транспонированные векторы
транспонированные векторы ![]() , соответственно.
, соответственно.
3. Определение коэффициента корреляции и его свойства
Подставим выражение (3) в функционал (2) с учетом (5), (6) и (8):
|
|
114) |
Здесь 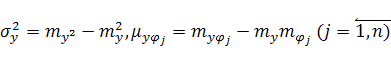 и, согласно (13), коэффициент детерминации
и, согласно (13), коэффициент детерминации ![]() определяется соотношением:
определяется соотношением:
|
|
(15) |
Из формулы (14) следует, что ![]() .
.
При  между СВ
между СВ ![]() либо не существует зависимости вида (1), либо эта зависимость носит иной характер (следует выбрать другие функции
либо не существует зависимости вида (1), либо эта зависимость носит иной характер (следует выбрать другие функции 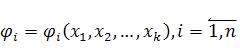 ).
).
При ![]() - функционал ошибки равен нулю
- функционал ошибки равен нулю ![]() и, следовательно, между СВ
и, следовательно, между СВ ![]() существует функциональная (в смысле вероятности) зависимость.
существует функциональная (в смысле вероятности) зависимость.
4. Частные случаи регрессии
Рассмотрим частные случаи регрессии.
I. Классическая парная линейная регрессия ![]() [2]:
[2]:
|
|
(16) |
В этом случае формулы (8), (12), (13) и (16) принимают вид:
|
|
(17) |
|
|
(18) |
|
|
(19) |
|
|
(20) |
Соотношения (16)—(20) были получены в работе [2] и соответствуют формулам классической парной линейной регрессии [1].
II. Линейная регрессия для трех СВ ![]() :
:
|
|
(21) |
В этом случае формулы (8), (12), (13) и (15) принимают вид:
|
|
(22) |
|
|
(23) |
|
|
(24) |
|
|
(25) |
|
|
(26) |
|
|
(27) |
III. Нелинейная квадратичная регрессия для двух СВ:
IV.
|
|
(28) |
Подставим функций ![]() в формулы (22), (26) и (27):
в формулы (22), (26) и (27):
|
|
(29) |
|
|
(30) |
|
|
(31) |
Заключение
В работе предложен метод получения теоретических параметров (коэффициентов) множественной регрессии и коэффициента детерминации путем минимизации функционала ошибки.
1. При выводе формул (8) и (13) не предполагались какие-либо ограничения, кроме условия (2). Следовательно, среди всех зависимостей вида (1) коэффициенты 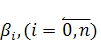 , найденные по (8) и (13), приводят к минимальной в смысле (2) погрешности аппроксимации.
, найденные по (8) и (13), приводят к минимальной в смысле (2) погрешности аппроксимации.
2. Получена формула (16) для вычисления коэффициента множественной детерминации.
3. Показано, что если ![]() , то между случайными величинами
, то между случайными величинами ![]() имеется функциональная зависимость вида (1).
имеется функциональная зависимость вида (1).
4. Приведены примеры получения формул для теоретических параметров парной линейной и квадратической зависимостей, а также множественной линейной регрессии трех случайных СВ.
Список литературы:
1.Доугерти К. Введение в эконометрику: Пер. с англ. М.:ИНФРА-М, 2001. — XIV, — 402 с., ISBN 5-86-225-458-7.
2.Орлов Н.Н., Орлова Е.Ю. Получение теоретических коэффициентов в уравнении парной линейной регрессии с помощью минимизации функционала ошибки// Материалы XXI международной заочной научно-практической конференции. (17 июня 2013 г.); Новосибирск: Изд. «СибАК», 2013. — С. 5—13. ISBN 978-5-4379-0302-5.
дипломов


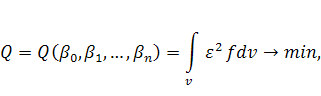


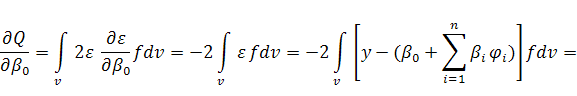
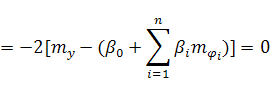

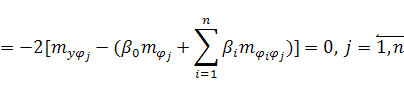


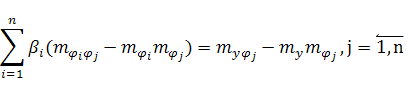
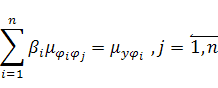
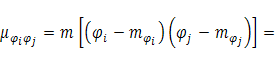

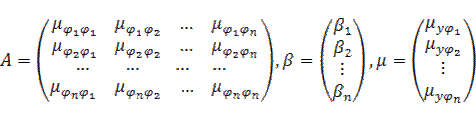


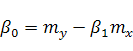
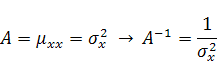

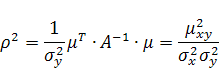
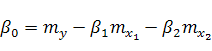
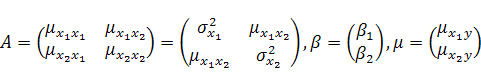
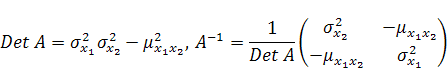
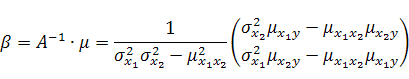
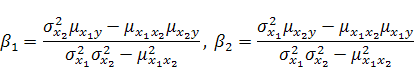
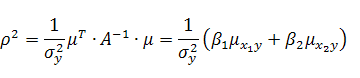
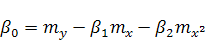


Оставить комментарий