Статья опубликована в рамках: XXII Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 15 июля 2013 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ОСОБЕННОСТИ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ ОСЦИЛЛЯТОРА ПОД ДЕЙСТВИЕМ ГАРМОНИЧЕСКИХ ИМПУЛЬСОВ СИЛЫ
Гетманова Елена Евгеньевна
канд. ф.-мат. наук, доцент кафедры физики, преподаватель OOO «Дистанционный репетитор», Москва
E-mail:
FORCED VIBRATION OF OSCILLATOR UNDER THE ACTION OF HARMONICS FORCE IMPULSES
Getmanova Elena
candidate of Phys.-Math. Science, Associate Prof. of Physics Deartment,
Educator of Company “DistTutor”, Moscow
АННОТАЦИЯ
В докладе аналитически и численно изучены особенности вынужденных колебаний гармонического осциллятора с различными начальными условиями под действием периодических гармонических импульсов силы. На сайте http://osciltheory.ucoz.com/ помещена Flash анимация рассмотренных колебаний.
ABSTRACT
Features of the forced oscillations of an pendulum with different initial conditions under action of periodic harmonics impulses of force have been considered. Animation of oscillations is shown on the site http://osciltheory.ucoz.com/.
Ключевые слова: Вынужденные периодические колебания, компьютерное Flash моделирование, периодические гармонические импульсы силы
Keywords: the forced periodic oscillations, Flash modeling, the periodic harmonics impulses of force.
В работе представлено исследование поведения осциллятора с различными начальными условиями под действием внешних периодических гармонических импульсов силы. Исследование проводилось аналитически (методом припасовывания [2, c. 62]), и численно. Метод припасовывания применялся для решения нелинейных задач [2, c. 62]. В работе данный метод используется при изучении поведения линейной системы под действием внешних периодических импульсов силы. Анимация, описанных в статье колебательных процессов, представлена на сайте http://osciltheory.ucoz.com/.
Рассмотрим осцилляторы (пружинные маятники), совершающие гармонические колебания под действием периодических импульсов силы меняющейся в интервалах ![]() , по закону
, по закону ![]() (
(![]() частота внешних периодических импульсов силы,
частота внешних периодических импульсов силы, ![]() время действия импульса силы,
время действия импульса силы, ![]() временной интервал между двумя последовательными силовыми воздействиями) по закону (рис. 1) (
временной интервал между двумя последовательными силовыми воздействиями) по закону (рис. 1) (![]() номер временного интервала действия импульса силы,
номер временного интервала действия импульса силы, ![]() номер временного интервала, где сила не действует).
номер временного интервала, где сила не действует).
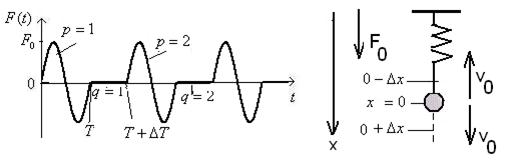
Рисунок 1. Периодические импульсы силы и осциллятор с различными начальными условиями
Сопротивление среды не учитывается, собственная частота колебаний осцилляторов равна ![]() . Отрицательное, положительное или нулевое начальные смещения
. Отрицательное, положительное или нулевое начальные смещения![]() , означают, что пружина сжата, растянута или не деформирована, соответственно. Отрицательное, положительное или нулевое значение начальной скорости
, означают, что пружина сжата, растянута или не деформирована, соответственно. Отрицательное, положительное или нулевое значение начальной скорости ![]() , означает, что она направлена противоположно, совпадает с направлением действия силы или равна нулю (рис. 1). Исследование проводилось для
, означает, что она направлена противоположно, совпадает с направлением действия силы или равна нулю (рис. 1). Исследование проводилось для
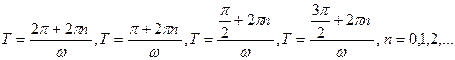 ,
, 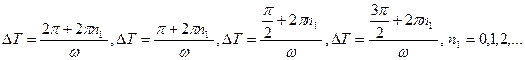 .
.
При рассмотренных значениях ![]() и
и ![]() , и соотношении частот и
, и соотношении частот и ![]()
![]() возможны периодические колебания с периодами
возможны периодические колебания с периодами ![]() ,
, ![]()
![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,а также колебания с нарастающей амплитудой.
,а также колебания с нарастающей амплитудой.
При соотношении частот и ![]()
![]() возможны периодические колебания с периодами
возможны периодические колебания с периодами ![]() ,
, ![]()
![]() ,
,![]()
![]() ,
,![]() ,а также колебания с нарастающей амплитудой.
,а также колебания с нарастающей амплитудой.
Например, при ![]() , амплитуда колебаний нарастает (http://osciltheory.ucoz.com/, «Гармонические импульсы 3»).
, амплитуда колебаний нарастает (http://osciltheory.ucoz.com/, «Гармонические импульсы 3»).
Зависимость смещения от времени в ![]() интервалах (свободные колебания) имеет вид
интервалах (свободные колебания) имеет вид
 .
.
При начальных условиях![]() , осциллятор находится в состоянии покоя в соответствующем
, осциллятор находится в состоянии покоя в соответствующем ![]() интервале (рис. 2а,
интервале (рис. 2а, ![]() ,
, ![]() ).
).
Зависимость смещения от времени в ![]() интервалах (вынужденные колебания)
интервалах (вынужденные колебания)
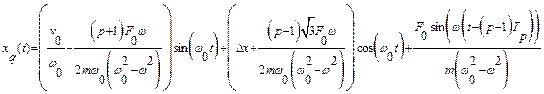
При начальных условиях![]() осциллятор совершает колебания с частотой вынуждающей силы в соответствующем
осциллятор совершает колебания с частотой вынуждающей силы в соответствующем ![]() интервале (рис. 2б,
интервале (рис. 2б, ![]() ,
,![]() ).
).
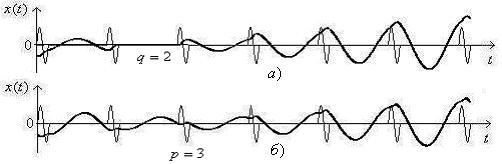
Рисунок 2. Осциллятор неподвижен в ![]() , совершает колебания с частотой вынуждающей силы в
, совершает колебания с частотой вынуждающей силы в ![]()
В случае периодических колебаний, существуют начальные условия, при которых маятник совершает колебания с частотой внешней силы в заданных ![]() или находится в состоянии покоя в заданных
или находится в состоянии покоя в заданных ![]() интервалах. Сдвиг фаз между колебаниями в соседних
интервалах. Сдвиг фаз между колебаниями в соседних ![]() (
(![]() ) интервалах, при указанных начальных условиях, равен
) интервалах, при указанных начальных условиях, равен ![]() .При
.При ![]() , период колебаний
, период колебаний ![]() . При начальных условиях
. При начальных условиях![]() колебания выполняются с частотой внешней силы в
колебания выполняются с частотой внешней силы в ![]() интервалах (рис. 3а), при
интервалах (рис. 3а), при ![]() - в
- в ![]() интервалах (рис. 3б). Сдвиг фаз между колебания осцилляторов, с приведенными выше начальными условиями, равен
интервалах (рис. 3б). Сдвиг фаз между колебания осцилляторов, с приведенными выше начальными условиями, равен ![]() .
.
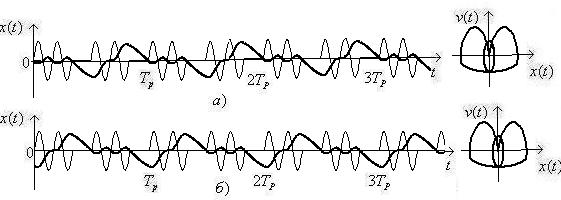
Рисунок 3. Колебания с частотой внешней силы в ![]() и
и ![]()
При начальных условиях![]() осциллятор неподвижен в
осциллятор неподвижен в ![]() интервалах (рис. 4а), при нулевых начальных условиях — в
интервалах (рис. 4а), при нулевых начальных условиях — в ![]() интервалах (рис. 4б).
интервалах (рис. 4б).
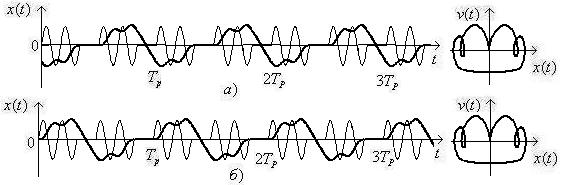
Рисунок 4. Осциллятор неподвижен в ![]() и
и ![]()
При ![]() , период колебаний
, период колебаний ![]() .
.
Существуют начальные фазы (начальные условия), при которых осциллятор совершает колебания с частотой вынуждающей силы в ![]() интервалах. Например, при
интервалах. Например, при ![]() колебания выполняются с частотой внешней силы в
колебания выполняются с частотой внешней силы в ![]() интервалах (рис. 5а), при
интервалах (рис. 5а), при ![]() — в
— в ![]() интервалах (рис. 5б),
интервалах (рис. 5б),
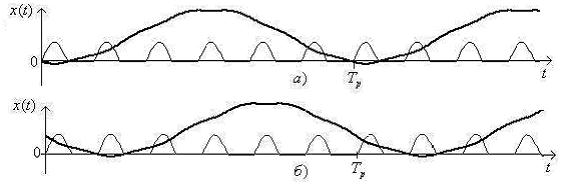
Рисунок 5. Колебания с частотой внешней силы в ![]() и
и ![]()
При 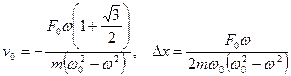 осциллятор неподвижен в
осциллятор неподвижен в ![]() (рис. 6а), при
(рис. 6а), при ![]() — в
— в ![]() интервалах (рис. 6б).
интервалах (рис. 6б).
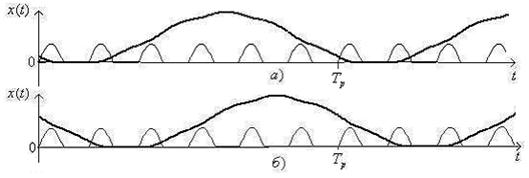
Рисунок 6. Осциллятор неподвижен в ![]() и
и ![]()
При ![]() , период равен
, период равен ![]() .
.
Существуют начальные условия, при которых осциллятор совершает колебания с частотой вынуждающей силы в ![]() интервалах. В частности, при
интервалах. В частности, при ![]() в
в ![]() интервалах колебания выполняются с частотой внешней силы (рис. 7а), при
интервалах колебания выполняются с частотой внешней силы (рис. 7а), при ![]() — в
— в ![]() интервалах (рис. 7б).
интервалах (рис. 7б).
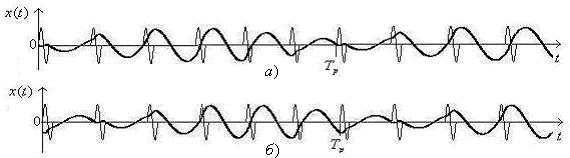
Рисунок 7. Колебания с частотой внешней силы в ![]() и
и ![]()
Аналогично можно определить начальные условия, при которых маятник будет неподвижен в любых заданных ![]() интервалах. Например, при
интервалах. Например, при ![]() в
в ![]() интервалах осциллятор неподвижен (рис. 8а). При
интервалах осциллятор неподвижен (рис. 8а). При ![]() в
в ![]() интервалах (рис. 8б).
интервалах (рис. 8б).
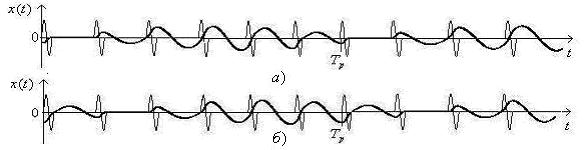
Рисунок 8. Осциллятор неподвижен в ![]() и
и ![]()
При ![]() ,период колебаний равен
,период колебаний равен ![]() .
.
При ![]() осциллятор неподвижен в в
осциллятор неподвижен в в ![]() интервалах (рис. 9а). При
интервалах (рис. 9а). При ![]() — в
— в ![]() интервалах (рис. 9б).
интервалах (рис. 9б).
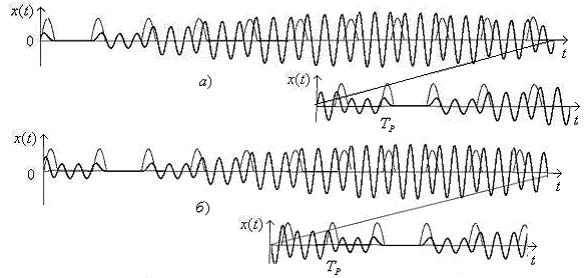
Рисунок 9. Осциллятор неподвижен в ![]() и
и ![]()
При ![]() колебания выполняются с частотой внешней силы в
колебания выполняются с частотой внешней силы в ![]() интервалах (рис. 10а), При
интервалах (рис. 10а), При ![]() — в
— в ![]() интервалах (рис. 10б).
интервалах (рис. 10б).
Можно определить начальные условия, при которых маятник будет неподвижен в любом наперед заданном ![]() интервале или двигаться под действием внешней силы в
интервале или двигаться под действием внешней силы в ![]() интервале.
интервале.
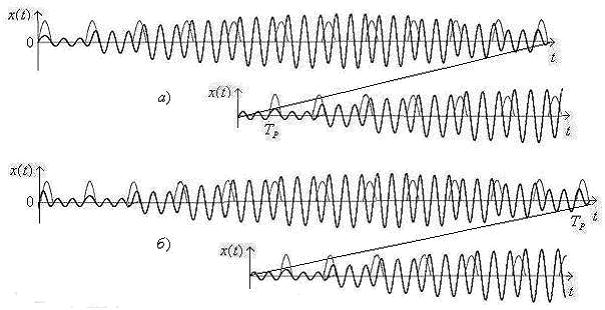
Рисунок 10. Колебания с частотой внешней силы в ![]() и
и ![]()
Явление нелинейных волн может быть феноменологически описано как вынужденные колебания совокупности несвязанных линейных осцилляторов, с модулированной начальной фазой, т. е. с начальными условиями, которые задают колебания с частотой вынуждающей силы в последовательных ![]() интервалах и состояние покоя в последовательных
интервалах и состояние покоя в последовательных ![]() интервалах.
интервалах.
На рис. 11 представлен профиль волны, составленной из осцилляторов с заданными начальными условиями,( ![]() ) в моменты времени
) в моменты времени ![]() (рис. 11а),
(рис. 11а), ![]() , (рис.11б),
, (рис.11б), ![]() , (рис. 11в). Темные кружки соответствуют осцилляторам, траектория колебаний которых показана на рис. 5, светлые — на рис. 6. На рис. 12 представлен профиль волны, составленной из осцилляторов с заданными начальными условиями (
, (рис. 11в). Темные кружки соответствуют осцилляторам, траектория колебаний которых показана на рис. 5, светлые — на рис. 6. На рис. 12 представлен профиль волны, составленной из осцилляторов с заданными начальными условиями (![]() ), в моменты времени
), в моменты времени ![]() , (рис.12а),
, (рис.12а), ![]() , (рис. 12б),
, (рис. 12б), ![]() , (рис. 12в). Темные кружки соответствуют осцилляторам, траектория колебаний которых показана на рис. 7, светлые — на рис. 8.
, (рис. 12в). Темные кружки соответствуют осцилляторам, траектория колебаний которых показана на рис. 7, светлые — на рис. 8.
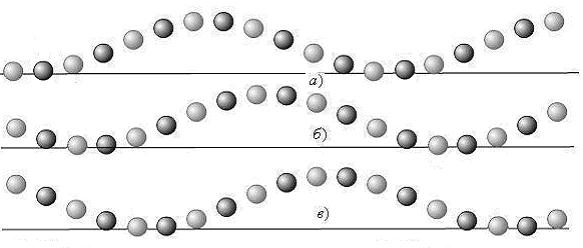
Рисунок 11. Профиль волны, составленной из осцилляторов
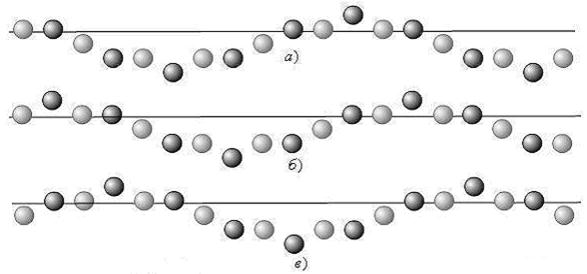
Рисунок 12. Профиль волны, составленной из осцилляторов
На рис. 13 представлен профиль волны, составленной из осцилляторов, с заданными начальными условиями (![]() ) в моменты времени
) в моменты времени ![]() , (рис. 13а),
, (рис. 13а), ![]() , (рис. 13б),
, (рис. 13б), ![]() , (рис. 13в), Темные кружки соответствуют осцилляторам, траектория колебаний которых показана на рис. 9, светлые — на рис. 10.
, (рис. 13в), Темные кружки соответствуют осцилляторам, траектория колебаний которых показана на рис. 9, светлые — на рис. 10.
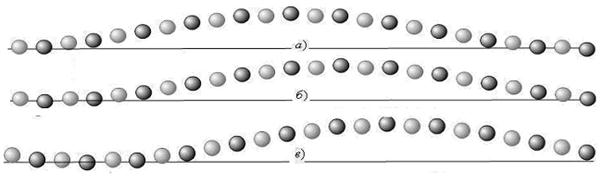
Рисунок 13. профиль волны, составленной из осцилляторов
Анимация колебаний приведена на сайте http://osciltheory.ucoz.com/.
Проведенное исследование показало, что при действии гармонических периодических импульсов на линейный осциллятор, при определенных соотношениях между временными интервала и частотами, возможен как режим нарастания амплитуды, так и периодических колебаний. Существуют начальные условия (начальная фаза), при которых осциллятор будет неподвижен в интервале между силовыми воздействиями или совершать колебания с частотой внешней силы в интервале действия силы. Явление нелинейных волн может быть феноменологически описано как вынужденные колебания совокупности несвязанных линейных осцилляторов, с модулированной начальной фазой.
Следует отметить, что вынужденные колебания линейных осцилляторов под действием внешних периодических импульсов постоянной или линейной нарастающих силы, также имеют или периодический характер, или амплитуда колебаний нарастает [1, c. 3] (http://osciltheory.ucoz.com/).
Список литературы:
1.Гетманова Е.Е. Колебания гармонического осциллятора под действием импульсов силы // Сборник научных трудов «SWorld». —т. 11, 2013.
2.Пановко Я.Г. Введение в теорию механических колебаний, M.: Наука, 1991, — 255 c.
дипломов


Оставить комментарий