Статья опубликована в рамках: XXI Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 17 июня 2013 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ПОЛУЧЕНИЕ ТЕОРЕТИЧЕСКИХ КОЭФФИЦИЕНТОВ В УРАВНЕНИИ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ С ПОМОЩЬЮ МИНИМИЗАЦИИ ФУНКЦИОНАЛА ОШИБКИ
Орлов Николай Николаевич
канд. ф.-м. наук, доцент, Институт коммерции и права, зав.кафедрой информатики и математики, г. Москва
E-mail: n_orloff@mail.ru
Орлова Елена Юрьевна
канд. техн. наук, доцент, Международный университет природы, общества и человека «Дубна», зав. заочным отделением филиала «Котельники», г. Дубна
E-mail: orlova.elena.urjevna@mail.ru
THEORETICAL COEFFICIENT CALCULATION IN LINEAR REGRESSION EQUATION BY MINIMIZING OF FUNCTIONAL VARIATIONS
Orlov Nikolai
PHd of Physical and Mathematical Sciences, Professor, Institute of Commerce and Law, Head of Department of Computer Science and Mathematics, Moscow
Orlova Elena
PHd of Science, Associate Professor, International University of Nature, Society and Man "Dubna", Head of the department of distance learning branch "Kotelniki", Dubna
АННОТАЦИЯ
Работа посвящена параметризации линейной регрессии. Представлен метод определения теоретических коэффициентов парной линейной регрессии путем минимизации функционала ошибки. Проанализировано соответствие полученных формул с результатами метода наименьших квадратов.
ABSTRACT
The work is devoted to the parameterization of the linear regression. The method of determining the theoretical Simple Linear Regression coefficients by minimizing the functional errors is presented in the work. The correspondence of the formulas obtained with the results of the method of least squares is analyzed.
Ключевые слова: линейная регрессия; ошибка аппроксимации; минимум функционала; коэффициенты уравнения; коэффициент корреляции.
Key words: linear regression, error of approximation; functional minimum, and the coefficients of the equation, the coefficient of correlation.
Введение
Во всех современных публикациях вывод эмпирических коэффициентов уравнения линейной регрессии основан на методе наименьших квадратов. Полученные коэффициенты являются оценками теоретических коэффициентов, хотя в теории должно быть наоборот — известны теоретические величины, для которых находятся эмпирические оценки.
1. Функционал ошибки и его минимум
Для определения эмпирических коэффициентов в уравнении линейной регрессии используется метод наименьших квадратов (МНК). В данной работе предлагается минимизировать функционал, который позволяет получить формулы для вычисления теоретических коэффициентов уравнения линейной регрессии.
Для простоты изложения все выкладки проводятся для случая парной линейной регрессии.
Пусть имеются две непрерывные случайные величины X и Y с функцией плотности распределения вероятности f(x,y). Требуется найти такую линейную аппроксимацию (1), в которой ошибка ![]() была бы наименьшей в «вероятностном» смысле:
была бы наименьшей в «вероятностном» смысле:
![]() , (1)
, (1)
здесь ![]() и
и ![]() —некоторые параметры, подлежащие определению.
—некоторые параметры, подлежащие определению.
Будем искать значения ![]() и
и ![]() путем минимизации следующего функционала:
путем минимизации следующего функционала:
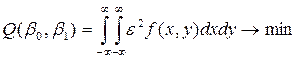 , (2)
, (2)
который представляет собой интегральную ошибку линейной аппроксимации:
![]() , (3)
, (3)
учитывающую совместную вероятность распределения ![]() случайных величин Х и Y
случайных величин Х и Y
Так как функции ![]() и
и ![]() для любых значений
для любых значений ![]()
![]() , то функционал
, то функционал ![]() имеет минимум, который находится из условий:
имеет минимум, который находится из условий:
 . (4)
. (4)
Найдем эти производные:
![]() , (5)
, (5)
![]() , (6)
, (6)
здесь введены следующие обозначения:
![]()
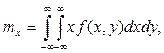
 (7)
(7)
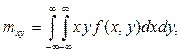
 (8)
(8)
Из решения системы линейных уравнений (5) и (6) получим формулы для вычисления неизвестных коэффициентов ![]() и
и ![]() :
:
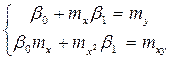 , (9)
, (9)
![]() , (10)
, (10)
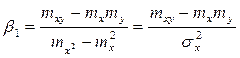 , (11)
, (11)
Где
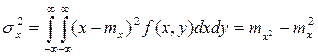 . (12)
. (12)
При выводе формул (10) и (11) не предполагались какие-либо ограничения, кроме условия (2). Следовательно, среди всех зависимостей вида (1) коэффициенты ![]() и
и ![]() , найденные по (10), (11), приводят к минимальной в смысле (2) погрешности аппроксимации.
, найденные по (10), (11), приводят к минимальной в смысле (2) погрешности аппроксимации.
2. Свойства ошибки аппроксимации
Из условий (5) и (6) вытекают следующие свойства случайной
величины ![]() :
:
1) 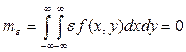 , (13)
, (13)
2)  , (14)
, (14)
3) 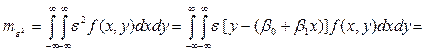
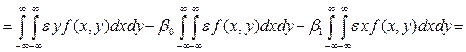
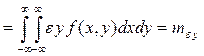 . (15)
. (15)
Подставим найденные значения ![]() и
и ![]() в основной интеграл
в основной интеграл ![]() :
:
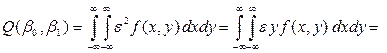
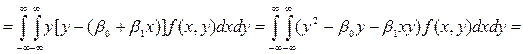
![]()

 , (16)
, (16)
где
 — коэффициент корреляции. (17)
— коэффициент корреляции. (17)
Так как 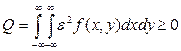 , то
, то
![]() или
или ![]() . (18)
. (18)
Очевидно, что при ![]() ошибка аппроксимации
ошибка аппроксимации
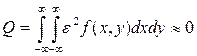 . (19)
. (19)
Из непрерывности подынтегральной функции ![]() следует, что
следует, что ![]() для всех
для всех ![]() , т. е. случайная величина Y является линейной функцией от случайной величины X:
, т. е. случайная величина Y является линейной функцией от случайной величины X:
![]() . (20)
. (20)
Из (17) следует, что при значении ![]() :
:
![]() или
или ![]() , (21)
, (21)
т. е.
![]() , (22)
, (22)
что равносильно утверждению, что между величинами X и Y нет линейной зависимости или эта зависимость имеет более сложный характер.
Случай выполнения равенства (19) равносилен следующему соотношению (некоррелированность случайных величин ![]() и
и ![]() ):
):
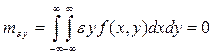 . (23)
. (23)
3. Переход к формулам классической парной линейной регрессии
Пусть имеются некоторые экспериментальные данные: ![]() , являющиеся репрезентативной выборкой объема «n». В этом случае, используя точечные оценки характеристик
, являющиеся репрезентативной выборкой объема «n». В этом случае, используя точечные оценки характеристик ![]() и
и ![]() , можно получить формулы для вычисления коэффициентов
, можно получить формулы для вычисления коэффициентов ![]() ,
, ![]() и
и ![]() (экспериментальных значений теоретических величин
(экспериментальных значений теоретических величин ![]() ,
, ![]() и
и ![]() ) соответственно [1, с. 62]:
) соответственно [1, с. 62]:
![]() , (24)
, (24)
![]() , (25)
, (25)
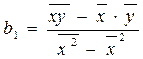 , (26)
, (26)
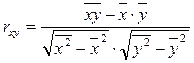 , (27)
, (27)
где 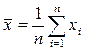 ,
,  ,
,
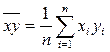 ,
,  . (28)
. (28)
Свойства (13), (14) и (15) имеют аналоги:
1) ![]() , (29)
, (29)
2) ![]()
![]() , (30)
, (30)
3)![]() . (31)
. (31)
Значение ошибки из экспериментальных данных определяются таким образом:
![]()
![]()
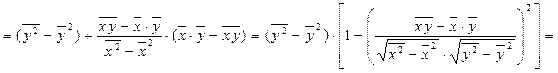
![]() . (32)
. (32)
Заключение
С помощью предложенного метода минимизации функционала ошибки:
1. При выводе формул (10) и (11) не предполагались какие-либо ограничения, кроме условия (2). Следовательно, среди всех зависимостей вида (1) коэффициенты ![]() и
и ![]() , найденные по (10), (11), приводят к минимальной в смысле (2) погрешности аппроксимации.
, найденные по (10), (11), приводят к минимальной в смысле (2) погрешности аппроксимации.
2. Получены формулы (10), (11) для вычисления теоретических коэффициентов ![]() и
и ![]() парной линейной регрессии.
парной линейной регрессии.
3. Показано, что если ![]() , то между случайными величинами X и Y имеется линейная зависимость.
, то между случайными величинами X и Y имеется линейная зависимость.
4. В случае репрезентативной выборки по формулам (25), (26) и (27) можно найти соответствующие (экспериментальные) приближения ![]() ,
, ![]() и
и ![]() теоретических величин
теоретических величин ![]() ,
, ![]() и
и ![]() .
.
5. Соотношения (25)—(26), полученные заменой в формулах (10)—(11) соответствующих величин их статистическими (выборочными) характеристиками (точечными оценками), совпадают с формулами, найденными по методу наименьших квадратов.
Список литературы:
1.Доугерти К. Введение в эконометрику: Пер. с англ. — М.:ИНФРА-М, 2001. — XIV, 402 с., ISBN 5-86-225-458-7.
дипломов


Оставить комментарий