СПОСОБЫ  РЕШЕНИЯ  ЗАДАЧ ЕДИНОГО  ГОСУДАРСТВЕННОГО  ЭКЗАМЕНА ПО  МАТЕМАТИКЕ  НА  НАХОЖДЕНИЕ  УГЛА МЕЖДУ  ПЛОСКОСТЯМИ

Ганеева  Айгуль  Рифовна

канд.  пед.  наук,  филиал  Казанского  (Приволжского)  Федерального  университета  в  г.  Елабуга,  доцент  кафедры  математического  анализа,  алгебры  и  геометрии

E-mail:  aigul_ganeeva@mail.ru

WAYS  TO  SOLVE  UNIFIED  STATE EXAMINATION  PROBLEMS IN  MATHEMATICS  ON  FINDING  OF  THE  CORNER  BETWEEN  THE  PLANES

Aygul  Ganeeva

Ph.  D.  in  Pedagogy,  Elabuga  branch  of  Kazan  (Volga  Region)  Federal  University,  associate  professor  in  mathematical  analysis,  algebra  and  geometry

АННОТАЦИЯ

Единый  государственный  экзамен  по  математике  на  протяжении  многих  лет  является  инновацией,  как  для  учащихся,  так  и  для  учи­телей,  так  как  каждый  год  появляются  все  новые  и  интересные  задачи.  Особо  новыми  и  нестандартными  задачами  являются  задачи  части  С.  В  данной  статье  рассмотрим  решение  задач  С2  единого  государст­венного  экзамена  по  математике  на  нахождения  угла  между  плоскостями.  Задачи  с  такой  проблемой  были  на  ЕГЭ  по  математике  в  2012  году. 

ABSTRACT

For  many  years  the  unified  state  examination  in  mathematics  is  an  innovation,  both  for  pupils,  and  for  teachers  as  every  year  there  appear  new  and  interesting  problems.  Especially  new  and  non-standard  tasks  are  problems  of  part  C.  In  this  article  we  will  consider  the  solution  of  problems  in  C2  of  the  unified  state  examination  on  mathematics  on  finding  a  corner  between  the  planes.  Such  problem,  were  on  Unified  State  Examination  in  mathematics  in  2012.

Ключевые  слова:  единый  государственный  экзамен;  математика.

Keywords:  unified  state  examination,  mathematics.

Задание  С2  Единого  государственного  экзамена  вот  уже  два  года  представляло  стереометрическую  задачу  на  определение  расстояний  или  углов  в  пространстве  между  объектами,  связанными  с  некоторым  многогранником.  При  решении  задач  на  расстояния  и  углы  в  стереометрии  обычно  используют  поэтапно  вычислительный  или  координатно-векторный  метод. 

Знание  учениками  нескольких  методов  решения  задач  имеет  свои  преимущества.  Так,  решив  задачу  одним  способом,  школьник  может  проверить  правильность  ответа  другим  способом.  Кроме  этого,  возможность  выбора  учащимися  разных  способов  решения  задачи  способствует  развитию  вариативного  мышления  у  школьников. 

Решая  задачу  о  нахождении  угла  между  плоскостями  в  курсе  стереометрии,  упор  делается  на  дополнительные  построения,  которые  позволяют  выделить  искомый  угол,  а  затем  рассчитать  его  величину.  Здесь  уместно  вспомнить  задачи  на  построение  сечений  многогран­ников,  которые  рассматриваются  в  10  классе  и  у  многих  школьников  вызывают  трудности.  Существование  формального  алгоритма  для  таких  построений  совершенно  не  облегчает  задачу,  поскольку  каждый  случай  достаточно  уникален,  а  любая  систематизация  лишь  усложняет  процесс.  Именно  поэтому  задача  C2  оценивается  в  два  балла.  Первый  балл  дается  за  правильные  построения,  а  второй  —  за  правильные  вычисления  и  собственно  ответ.

Преимуществами  применения  поэтапного  вычислительного  метода  являются:  высокая  наглядность  дополнительных  построений,  которые  подробно  изучаются  на  уроках  геометрии  в  10—11  классах;  значительное  сокращение  объема  вычислений  при  правильном  подходе.

Рассмотрим  определение  двугранного  угла

Рисунок  1.

Определение  1.  Двугранный  угол,  образованный  полуплос­костями  измеряется  величиной  его  линейного  угла,  получаемого  при  пересечении  двугранного  угла  плоскостью,  перпендикулярной  его  ребру.

ÐAOB  —  линейный  угол  двугранного  угла  с  ребром  СD.  Так  как  ОА^СD,  ОВ^СD,  то  плоскость  АОВ  перпендикулярна  к  прямой  СD  (рис.  1).

Чтобы  построить  линейный  угол  двугранного  угла,  нужно  взять  на  линии  пересечения  плоскостей  произвольную  точку,  и  в  каждой  плоскости  провести  к  этой  точке  луч  перпендикулярно  линии  пересечения  плоскостей.  Угол,  образованный  этими  лучами  и  есть  линейный  угол  двугранного  угла.

Задача.  Дана  шестиугольная  правильная  призма  А…F₁.  Сторона  основания  равна  2,  а  высота  4,  СL:LC₁=3:1,  FK:KF₁=1:3.  Найти  угол  между  плоскостью  KLB  и  плоскостью  основания  призмы.

Решение. 

1.         способ  (Используя,  определение  1).  LK∩CF=P  (рис.  2).

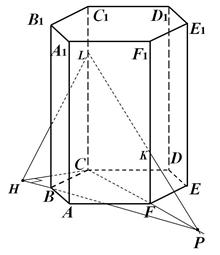
Рисунок  2.

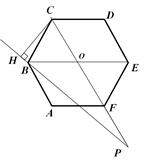
Рисунок  3.

Плоскость  основания  призмы  пересекается  с  плоскостью  BKL  по  прямой  ВР.  CL=3,  FK=1,  СF=4.

Из  подобия  треугольников  LCP  и  KFP  следует    Пусть  РF=x,  тогда  СР=х+4  и  поучим  уравнение    Т.  е.  РF=2,  тогда  СР=6. 

Из  треугольника  СВР  по  теореме  косинусов  найдем  ВР  (рис.  3).

ВР²=СВ²+СР²  –  2СВ·СР  соsÐВСР. 

Найдем  площадь  треугольника  ВСР  двумя  способами  и  приравняем  полученные  выражения  площадей.

где:  СН  —  высота  треугольника  ВСР.

Угол  LHC  является  искомым  углом,  т.  к.  LH^BP  и  CH^BP.

Найдем  LH  и  косинус  угла  из  треугольника  CHL.

Ответ: 

К  недостаткам  использования  поэтапного  вычислительного  метода  можно  отнести  необходимость:  знать  большое  количество  формул  из  стереометрии  и  планиметрии;  строить  дополнительные  построения.  И  это  может  оказаться  серьезной  проблемой  даже  для  хорошо  подготовленных  учеников.

Если  у  учащихся  хорошее  стереометрическое  воображение,  проблем  с  дополнительными  построениями  не  возникнет.  Остальным  школьникам  предлагаем  отказаться  от  традиционного  геометрического  метода  и  рассмотреть  более  эффективный  метод  координат. 

2.         способ.  Метод  координат.

Задачу  о  нахождении  угла  между  плоскостями  α  и  β,  заданными  в  прямоугольной  декартовой  системе  координат  уравнениями  a₁x+b₁y+c₁z+d=0  и  a₂x+b₂y+c₂z+d=0  соответственно,  удобнее  свести  к  задаче  о  нахождении  угла  между  векторами  их  нормалей    используя  формулу 

Решим  задачу  вторым  способом. 

Введем  систему  координат  (рис.  4).  Начало  координат  поместим  в  точке  O,  где  О  —  это  центр  нижнего  основания.  Оси  координат  x,  y,  z  направим  по  лучам  ОМ,  ОЕ,  ОО₁  соответственно,  где  М  —  середина  АF,  O₁  —  центр  верхнего  основания  призмы. 

Укажем  координаты  трех  точек:

B(0,  —  2,0  ),  К(,  1,  1),  L

Любую  прямую,  перпендикулярную  плоскости,  кратко  называют  нормалью  к  плоскости.  Любой  вектор,  лежащий  на  этой  прямой,  называют  нормальным  вектором  этой  плоскости.  Нетрудно  заметить,  что  угол  между  плоскостями  равен  между  нормальными  векторами  к  данным  плоскостям. 

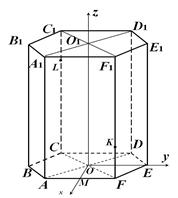
Рисунок  4.

Плоскость  основания  призмы  совпадает  с  плоскостью:  z=0.  Нормальный  вектор  данной  плоскости  имеет  вид

Найдем  уравнение  плоскости  ax+by+cz+d=0,  проходящей  через  точки  B,  К,  L. 

Отсюда

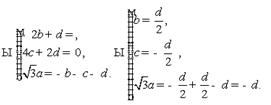
Итак, 

Имеем,  в  частности,  такое  уравнение 

Нормальным  вектором  этой  плоскости  будет 

Задачи  для  самостоятельного  решения. 

Дана  шестиугольная  правильная  призма  А…F₁.  Сторона  основания  равна  2,  а  высота  4.

1. ВL:LВ₁=3:1,  K  середина  АА₁.  Найти  угол  между  плоскостью  KLМ  и  плоскостью  основания  призмы,  где  М  середина  ВС.  Найти  угол  между  плоскостью  CKL  и  плоскостью  основания  призмы.  Найти  угол  между  плоскостью  DKL  и  плоскостью  основания  призмы.  Найти  угол  между  плоскостью  FKL  и  плоскостью  основания  призмы.

2. СL:LC₁=3:1,  AK:KA₁=1:3.  Найти  угол  между  плоскостью  KLM  и  плоскостью  основания  призмы,  где  М  середина  ВС.  Найти  угол  между  плоскостью  DKL  и  плоскостью  основания  призмы.

3. CL:LC₁=3:1,  K  середина  АА₁.  Найти  угол  между  плоскостью  EKL  и  плоскостью  основания  призмы.

4. L  середина  CC₁,  AK:KA₁=1:3.  Найти  угол  между  плоскостью  EKL  и  плоскостью  основания  призмы.

5. СL:LC₁=3:1,  K  середина  АА₁.  Найти  угол  между  плоскостью  EKL  и  плоскостью  основания  призмы.  Найти  угол  между  плоскостью  ВKL  и  плоскостью  основания  призмы.

6. L  середина  CC₁,  FK:KF₁=1:3.  Найти  угол  между  плоскостью  АKL  и  плоскостью  основания  призмы.  Найти  угол  между  плоскостью  ВKL  и  плоскостью  основания  призмы. 

7. СL:LC₁=3:1,  FK:KF₁=1:3.  Найти  угол  между  плоскостью  АKL  и  плоскостью  основания  призмы.  Найти  угол  между  плоскостью  ВKL  и  плоскостью  основания  призмы.  Найти  угол  между  плоскостью  KLМ  и  плоскостью  основания  призмы,  где  М  середина  AF.

8. СL:LC₁=3:1,  K  середина  FF₁.  Найти  угол  между  плоскостью  АKL  и  плоскостью  основания  призмы.  Найти  угол  между  плоскостью  ВKL  и  плоскостью  основания  призмы.

Список  литературы:

1. Атанасян  Л.С.  Геометрия.  Учебник  для  10—11  классов.  —  М.:  Просвещение,  2009.  —  255  с.

2. ЕГЭ  —  2013.  Математика:  типовые  экзаменационные  варианты:  30  вариантов  /  под  ред.  А.Л.  Семенова,  И.В.  Ященко.  —  М.:  Национальное  образование,  2012.  —  192  с.

3. Материалы  курса  «Готовим  к  ЕГЭ  хорошистов  и  отличников»:  лекции  5—8  /  А.Н.  Корняков,  А.А.  Прокофьев.  —  М.:  Педагогический  университет  «Первое  сентября»,  2012.  —  100  с.