Статья опубликована в рамках: XLVI Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 24 июня 2015 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
КОНЕЧНОЭЛЕМЕНТНОЕ МОДЕЛИРОВАНИЯ ПРОЦЕССА РАСПРОСТРАНЕНИЯ УПРУГИХ ВОЛН В ОДНОМЕРНОЙ СРЕДЕ СО СФЕРИЧЕСКОЙ СИММЕТРИЕЙ
Гуш Максим Николаевич
аспирант, кафедра прикладной математики
Новосибирского государственного технического университета,
РФ, г. Новосибирск
FINITE-ELEMENT MODELING OF ELASTIC WAVES IN ONE-DIMENSIONAL MEDIUM WITH SPHERICAL SYMMETRY
Maxim Gush
postgraduate student Department of Applied Mathematics
Novosibirsk State Technical University,
Russia, Novosibirsk
АННОТАЦИЯ
В данной статье рассматривается конечноэлементное моделирование процесса распространения упругих волн в одномерной среде, обладающей сферической симметрией. Приводятся вывод эквивалентной вариационной постановки и построение конечноэлементного аналога. Оценивается порядок аппроксимации разработанной схемы.
ABSTRACT
The article discusses the finite element modeling of elastic wave propagation in one-dimensional medium with spherical symmetry. An equivalent variation formulation has been developed and finite element discretization has been carried out. The order of approximation has been estimated.
Ключевые слова: упругие волны; метод конечных элементов; вариационная постановка; дискретный аналог.
Keywords: elastic waves; finite element method; variation formulation; finite element discretization.
Распространение упругих волн в изотропной среде обладающей сферической симметрией описывается одномерным волновым уравнением и является наиболее простым случаем распространения упругих волн. При этом в силу симметрии в такой среде будут наблюдаться только продольные упругие волны, в которых смещение направлено вдоль вектора распространения самой волны. В практических задачах среды, обладающие сферической симметрией, встречаются крайне редко, однако, данная задача может быть использована для исследования качественного характера получаемых численных решений в задачах распространения упругих волн и для отладки более сложных процедур (моделирование распространения упругих волн в двух- и трёхмерных средах, решение обратной задачи сейсмической разведки и т. д.).
Математическая модель одномерной задачи в сферических координатах описывается следующим уравнением [1, с. 513]:
|
|
(1) |
где: u(r,t) — деформация среды в точке r,
![]() (r,t) — функция задающая внешние силы,
(r,t) — функция задающая внешние силы, ![]()
![]() — плотность,
— плотность,
![]() — модуль сдвига,
— модуль сдвига,
![]() — коэффициент Пуассона.
— коэффициент Пуассона.
Начальные условия:
|
|
(2) |
Краевые условия:
|
|
(3) |
Получим вариационную формулировку в форме уравнения Галёркина [2, с. 84]. Для этого потребуем, чтобы невязка дифференциальных уравнений была ортогональна (в смысле скалярного произведения пространства ![]() ) некоторому пространству
) некоторому пространству ![]() пробных функций
пробных функций ![]() , т. е.
, т. е.
|
|
(4) |
Расписывая скалярное произведение, получим:
|
|
(5) |
По свойствам дивергенции:
|
|
(6) |
где: ![]() — скалярное поле,
— скалярное поле,
![]() — векторное поле. Тогда справедливо:
— векторное поле. Тогда справедливо:
|
|
(7) |
По теореме о дивергенции:
|
|
(8) |
где ![]() — вектор нормали к поверхности
— вектор нормали к поверхности ![]() .
.
Учитывая (8), соотношение (7) примет вид:
|
|
(9) |
Тогда
|
|
(10) |
Подставим полученные соотношения (10) в (5):
|
|
(11) |
Поскольку на границе ![]() краевыми условиями не определяется значение
краевыми условиями не определяется значение ![]() , то слагаемое
, то слагаемое ![]() следует исключить из уравнения, потребовав, чтобы пространство пробных функций Φ содержало только функции, которые принимали бы только нулевые значения на границе
следует исключить из уравнения, потребовав, чтобы пространство пробных функций Φ содержало только функции, которые принимали бы только нулевые значения на границе ![]() . Обозначим их
. Обозначим их ![]() .
.
Обратим внимание, что в полученное выше уравнение входят производные пробных функций ![]() . Поэтому в качестве пространства пробных функций Φ мы можем выбрать
. Поэтому в качестве пространства пробных функций Φ мы можем выбрать ![]() — пространство функций, имеющих суммируемые с квадратом производные и равные 0 на границе
— пространство функций, имеющих суммируемые с квадратом производные и равные 0 на границе ![]() .
.
Таким образом, получаем систему вариационных уравнение вида:
|
|
(12) |
В силу (3) приходим к уравнению
|
|
(13) |
Сделаем дискретизацию по времени [2, c. 364]. Будем полагать, что ось времени ![]() разбита на так называемые временные слои значениями
разбита на так называемые временные слои значениями ![]() ,
, ![]() , а значения искомой функции
, а значения искомой функции ![]() на k-м временном слое обозначим через
на k-м временном слое обозначим через ![]() , которые не зависят от времени, но остаются функциями пространственных координат.
, которые не зависят от времени, но остаются функциями пространственных координат.
Рассмотрим процедуру построения неявной четырехслойной схемы для решения дифференциального уравнения гиперболического типа.
Представим искомое решение ![]() на интервале
на интервале ![]() в следующем виде:
в следующем виде:
![]()
где функции ![]() являются значениями искомой функции при
являются значениями искомой функции при ![]() , а функции
, а функции ![]() являются кубическими полиномами и имеют вид:
являются кубическими полиномами и имеют вид:
|
|
(15) |
|
|
(16) |
|
|
(17) |
|
|
(18) |
Применим представление (14) для аппроксимации второй производной по времени в уравнениях на временном слое ![]() :
:
|
|
(19) |
|
|
(20) |
Подставим (20) в уравнения (13) и получим:
|
|
(21) |
Перейдём к конечноэлементной СЛАУ. При построении численного решения по методу Галёркина минимум невязки ищется не на пространствах ![]() и
и ![]() , а на аппроксимирующих их конечномерных подпространствах
, а на аппроксимирующих их конечномерных подпространствах ![]() и
и ![]() . При этом конечномерное пространство
. При этом конечномерное пространство ![]() , подпространствами которого являются
, подпространствами которого являются ![]() и
и ![]() , мы определим как линейное пространство, натянутое на базисные функции
, мы определим как линейное пространство, натянутое на базисные функции ![]() .
.
Заменим функции ![]() аппроксимирующие их функции
аппроксимирующие их функции ![]() , а функцию
, а функцию ![]() функцией
функцией ![]() :
:
|
|
(22) |
Любая функция ![]() может быть представлена в виде линейной комбинации базисных функций пространства
может быть представлена в виде линейной комбинации базисных функций пространства ![]() :
:
|
|
(23) |
Функции ![]() так же можно представить в виде линейной комбинации базисных функций пространства
так же можно представить в виде линейной комбинации базисных функций пространства ![]() :
:
|
|
(24) |
причём ![]() компонент векторов весов
компонент векторов весов![]()
![]() должны быть фиксированы и могут быть определены из условий
должны быть фиксированы и могут быть определены из условий
![]()
Подставляя (23) и (24) в (22) получим дискретный аналог для (13):
|
|
(26) |
В результате мы получили систему из ![]() уравнений с
уравнений с ![]() неизвестными
неизвестными ![]() . Чтобы определить матрицу и вектор правой части полученной конечноэлементной СЛАУ, пронумеруем её уравнения и неизвестные следующим образом.
. Чтобы определить матрицу и вектор правой части полученной конечноэлементной СЛАУ, пронумеруем её уравнения и неизвестные следующим образом.
Систему уравнений (26) можно записать в матричном виде:
|
|
(27) |
где
|
|
(28) |
|
|
(29) |
Используемые в МКЭ базисные функции являются финитными, т.е. каждая функция ![]() не равна 0 только на нескольких примыкающих к определяющему её i-му узлу конечных элементах
не равна 0 только на нескольких примыкающих к определяющему её i-му узлу конечных элементах ![]() . Следовательно, для фиксированной функции
. Следовательно, для фиксированной функции ![]() только небольшое число функций
только небольшое число функций ![]() отличны от 0 в подобласти, где
отличны от 0 в подобласти, где ![]() . Тогда из соотношений (28) очевидно, что в каждой строке матрицы
. Тогда из соотношений (28) очевидно, что в каждой строке матрицы ![]() содержится мало ненулевых элементов, поэтому для хранения и обработки матрицы будет использован разреженный формат хранения.
содержится мало ненулевых элементов, поэтому для хранения и обработки матрицы будет использован разреженный формат хранения.
Поскольку базисные функции кусочно-полиномиальные, то интегралы в (28) практично вычислять, как сумму интегралов по конечным элементам ![]() на которые разбита расчётная область и тогда матрица
на которые разбита расчётная область и тогда матрица ![]() представляется в виде суммы вкладов
представляется в виде суммы вкладов ![]() от соответствующих конечных элементов
от соответствующих конечных элементов ![]() :
:
|
|
(30) |
При этом фактически все ненулевые компоненты матрицы ![]() (размера
(размера ![]() ) можно разместить в локальной матрице
) можно разместить в локальной матрице ![]() размера
размера ![]() , где
, где ![]() – количество базисных функций, отличных от нуля на конечном элементе
– количество базисных функций, отличных от нуля на конечном элементе ![]() .
.
Локальные лагранжевы базисные функции на конечном элементе ![]() представляются в виде [2, c. 68]:
представляются в виде [2, c. 68]:
|
|
(31) |
Каждая базисная функция равна единице в узле соответствующем её номеру и нулю в остальных.
Локальные матрицы для линейных лагранжевых базисных функций будем вычислять численно по схеме Гаусс-4.
Протестируем аппроксимацию решения по пространству.
Расчётная область: ![]() ;
; ![]()
Параметры среды: ![]() ;
;
Аналитическое решение:

Определим по правилу Рунге порядок аппроксимации:
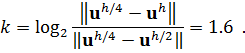
Вывод: Решение с дроблением сетки по пространству сходится к правильному. Порядок пространственной аппроксимации ![]() совпадает с теоретическим.
совпадает с теоретическим.
Протестируем аппроксимацию решения по времени.
Расчётная область: ![]() ;
; ![]()
Расчётный интервал времени: ![]() ;
; ![]()
Параметры среды: ![]() ;
;
Аналитическое решение:
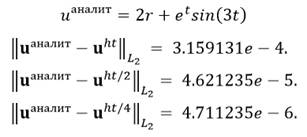
Определим по правилу Рунге порядок аппроксимации:
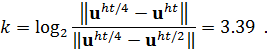
Вывод: Решение с дроблением сетки по времени сходится к правильному. Порядок аппроксимации по времени ![]() совпадает с теоретическим.
совпадает с теоретическим.
Список литературы:
1.Новацкий В. Теория упругости: учебное пособие. М.: «Мир», 1975. — 872 с.
2.Соловейчик Ю.Г., Рояк М.Э., Персова М.Г. Метод конечных элементов для решения скалярных и векторных задач: учебное пособие. Новосибирск: Изд-во НГТУ, 2007. — 896 с.
дипломов




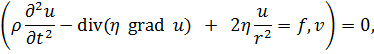

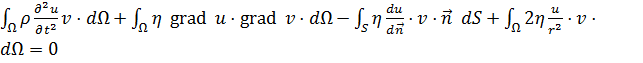 .
.
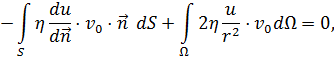


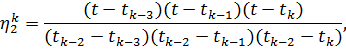
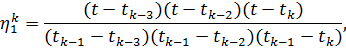
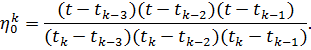
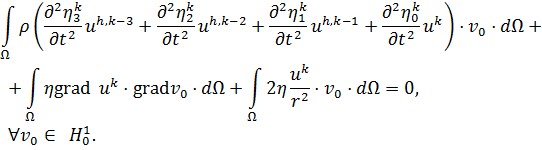
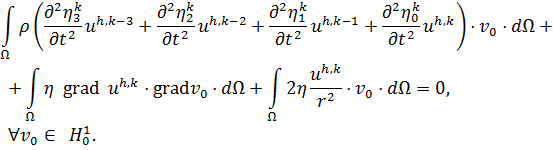

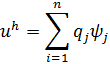
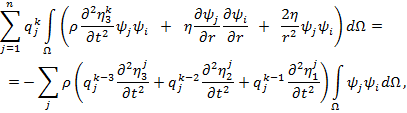



Оставить комментарий