РЕШЕНИЕ  НАЧАЛЬНО-ГРАНИЧНЫХ  ЗАДАЧ  ДЛЯ  ВОЛНОВОГО  УРАВНЕНИЯ  МЕТОДОМ  ИНТЕГРАЛЬНЫХ  ПРЕОБРАЗОВАНИЙ  ФУРЬЕ

Фахретдинова  Дилара  Ильдаровна

студент  4  курса  Стерлитамакского  филиала  Башкирского  Государственного  Университета,  РФ,  г.  Стерлитамак

E -mail:  dilaragirl09@bk.ru

Сабитова  Юлия  Камилевна

канд.  физ.-мат.  наук,  доцент  Стерлитамакского  филиала  Башкирского  Государственного  Университета,  РФ,  г.  Стерлитамак

E-mail: 

SOLUTION  OF  THE  INITIAL-BOUNDARY  VALUE  PROBLEMS  FOR  THE  WAVE  EQUATION  FOURIER  INTEGRAL  METHOD

Dilara  Fakhretdinova

4th  year  student  of  Sterlitamak  Branch  the  Bashkir  State  University,  Russia,  Sterlitamak

Julia  Sabitova

candidate  of  physico-mathematical  sciences,  associate  professor  of  Sterlitamak  Branch  the  Bashkir  State  University,  Russia,  Sterlitamak

АННОТАЦИЯ

В  данной  статье  решены  начально-граничные  задачи  для  однородного  и  неоднородного  волновых  уравнений,  методом  интегральных  преобразований  Фурье.

ABSTRACT

This  article  addressed  the  initial-boundary  value  problems  for  homogeneous  and  inhomogeneous  wave  equation,  the  Fourier  integral  method.

Ключевые  слова :  методом  интегральных  преобразований  Фурье;  начально-граничная  задача;  преобразование  Фурье.

Keywords:  Fourier  integral  method;  initial-boundary  problem;  Fourier  transform.

Если  функция  ,  является  непрерывной,  кусочно-гладкой  из  класса  абсолютно  интегрируемых  на  функций,  то  справедлива  интегральная  формула  Фурье 

Назовем  образом  Фурье  функции    функцию

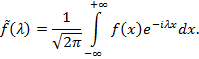
В  силу  интегральной  формулы  Фурье  функция    может  быть  восстановлена  с  помощью  формулы

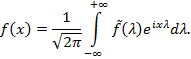
Переход  от    к    называется  интегральным  преобразованием  Фурье,  а  переход  от    к    называется  обратным  преобразованием  Фурье.

Если  же  функция    задана  на  полупрямой  ,  то  можно  рассматривать  косинус-образ  Фурье

переход  от  которого  к  оригиналу    осуществляется  по  формуле

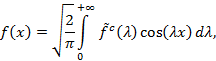
и  синус  —  образ  Фурье

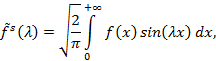
переход  от  которого  к  оригиналу    осуществляется  по  формуле

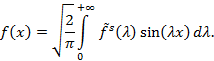
Основными  свойствами  преобразования  Фурье  является:

1.линейность,  т.  е.    (произвольные  постоянные);

2.преобразование  частных  производных,  т.  е.  если    и  преобразование  Фурье  проводится  по  переменной  x,  то 

,

а  образы  частных  производных  по  t  даются  формулами

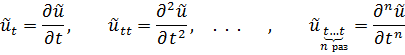
Под  действием  преобразования  Фурье  операция  дифференцирования  по  x  заменяется  умножением.  Этот  важный  факт  используется  при  решении  граничных  задач  для  дифференциальных  уравнений  с  частными  производными.

Пример  1 .  Решить  краевую  задачу

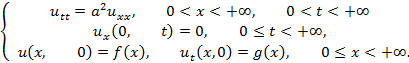
Решение.   Применим  косинус  —  преобразование  Фурье  по  переменной  x.  Пусть 

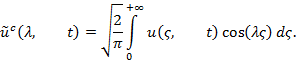
Проверим  выполнение  граничного  условия    Имеем

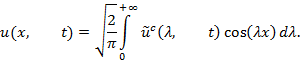
Дифференцирование  по  x  дает

откуда  следует,  что  .  Тогда,  учитывая,  что

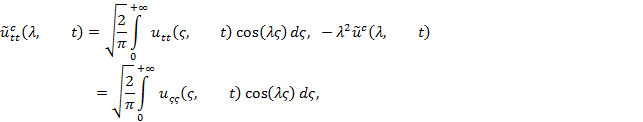
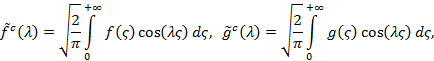
приходим  к  задаче  Коши  для  дифференциального  уравнения  второго  порядка

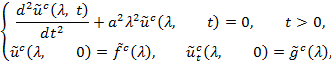
для  определения  функции  .  Решение  этой  задачи  имеет  вид

Искомую  функцию    находим  с  помощью  обратного  косинус  —  преобразования  Фурье:

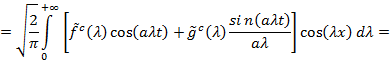
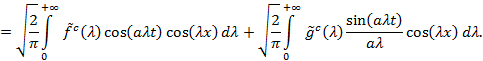
Рассмотрим  два  случая.

1)  .  Тогда

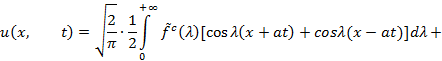
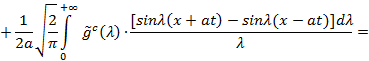
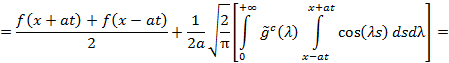
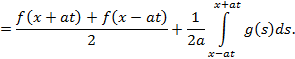
2)  .  Тогда

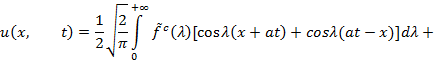
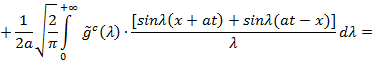
Поскольку  функция  g(x)  определена  только  для  положительных  значений  x,  то  нужно  преобразовать  последний  интеграл:

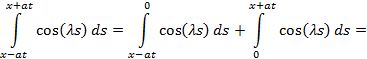
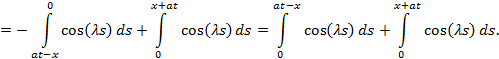
Теперь

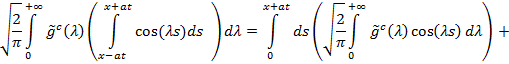
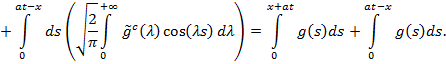
Искомое  решение  имеет  вид:

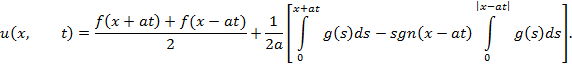
Замечание  1 .  В  качестве  функций    могут  быть,  например,  взяты  функции    и  т.  д.

Замечание  2 .  Для  решения  задач  на  полуограниченной  прямой  с  граничными  условиями    нужно  воспользоваться  синус-преобразованием  Фурье,  так  как,  если    то 

Рассмотрим  более  сложную  задачу  на  применение  преобразования  Фурье.

Пример  2.   Решить  задачу  Коши

Решение.   Применим  к  левой  и  правой  частям  уравнения  с  частными  производными  преобразования  Фурье  по  переменной  x.  Получим  неоднородное  дифференциальное  уравнение  второго  порядка  с  нулевыми  условиями 

Воспользуемся  методом  Дюамеля  решения  этой  задачи  Коши.  Решим  вспомогательную  задачу  Коши.

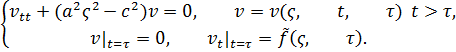
Тогда  решение  исходной  преобразованной  задачи  дается  формулой 

где 

Отсюда

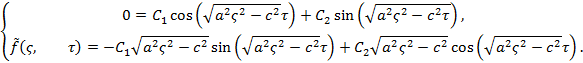
Обозначим    Тогда

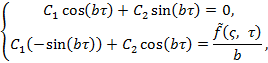
откуда

Значит,

т.  е.

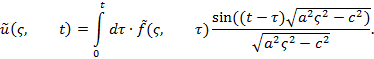
По  формуле  обращения  преобразования  Фурье

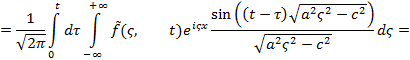
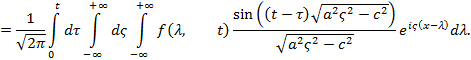
В  теории  функций  Бесселя  имеет  место  формула

Сделаем  в  этом  равенстве  замену 

Отсюда    Теперь  будем  иметь

Сделаем  в  интеграле  замену  переменной    откуда  Тогда

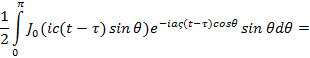
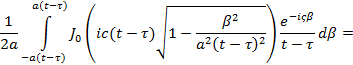
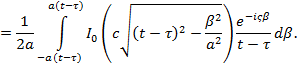
Следовательно, 

Положим 

Тогда

В  силу  интегральной  формулы  Фурье 

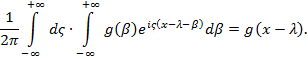
В  силу  определения  функции  ,  получим:

=

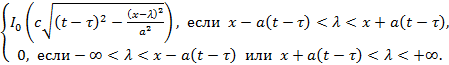
Окончательно

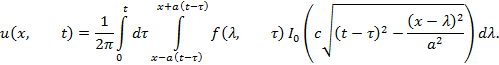
Список  литературы:

1.Будак  Б.М.,  Самарский  А.А.,  Тихонов  А.Н.  Сборник  задач  по  математической  физике.  М.:  Наука,  1978.

2.Сабитов  К.Б.  Уравнения  математической  физики.  М.:  ФИЗМАТЛИТ,  2013.

3.Бейтмен  Г.,  Эрдейе  А.  Высшие  трансцендентные  функции  т.  2.  М.:  Наука  1966,  —  296  с.