ЗАКОН ДВИЖЕНИЯ ПЛОСКОГО ТЕЛА ИДЕАЛЬНО КРУГЛОЙ ФОРМЫ ПРИ ВЗАИМОДЕЙСТВИИ СО СТРУНОЙ, ЛЕЖАЩЕЙ НА УПРУГОМ ОСНОВАНИИ

Андрианов Валерий Леонидович

канд. ф.-м. наук, доцент ННГУ, г. Н. Новгород

Яковлев Роман Николаевич

аспирант, ННГУ, г. Н. Новгород

E-mail: rn.yakovlev@gmail.com

THE LAW OF MOTION OF A FLAT BODY PERFECTLY ROUND SHAPE IN THE INTERACTION WITH THE STRING ON AN ELASTIC BASE

Valery Andrianov

Candidate of Physico-mathematical Sciences,

Associate Professor Lobachevsky

State University of Nizhny Novgorod, Nizhny Novgorod

Roman Yakovlev

Graduate student Lobachevsky

State University of Nizhny Novgorod, Nizhny Novgorod

Аннотация

В данной работе рассматривается самосогласованная задача о взаимодействии плоского тела идеально круглой формы со струной, лежащей на упругом основании.

Целью работы является вывод закона движения плоского тела идеально круглой формы, и моделирование распространения волны в струне, после взаимодействия с диском. Задача решалась методами операционного исчисление. Этот метод был выбран в силу его компактности, удобства и простоты при решении дифференциальных уравнений с частными производными.

ABSTRACT

In this paper we consider the self-consistent problem of the interaction of a flat body perfectly round in shape with the string on an elastic foundation.

The aim is to conclude the law of motion of a flat body perfectly round, and modeling of wave propagation in the string, after the interaction with the disk. The problem was solved by methods of operational calculus. This method was chosen because of its compactness, convenience and simplicity in the solution of differential equations with partial derivatives.

Ключевые слова: диск; струна; операционное исчисление; уравнение колебаний струны.

Keywords: disk; string; operational calculus; the equation of string vibration.

Пусть на покоящуюся в начальный момент времени  струну, лежащую на упругом основании, малые поперечные колебания, которой описываются уравнением:

,                                                                 (1)

                                                                           (2)

где  — скорость распространения поперечных волн в струне, величина  характеризует упругие свойства системы, «наезжает» плоское тело круглой формы с идеально гладкой поверхностью (диск радиуса ) и массой (Рис. 1).

Рис. 1 Взаимодействие диска со струной

Уравнение движения «низшей» точки диска задается уравнением:

где  — искомая функция, которая определяется из условия динамического взаимодействия диска со струной. Тогда в момент времени  в указанной системе координат уравнение «низшей» части границы тела имеет вид:

Из условия  , как легко видеть, следует, что скорость движения «точки контакта» , где

на некотором интервале времени  превышает критическую (при ), следовательно  при . Из того, что сила реакции струны  направлена по нормали к поверхности тела следует равенство углов, обозначенных через α и, следовательно, в движущейся «точке»  должны выполняться условия непрерывности и «нормального отражения» струны, т.е.:

Уравнение поперечных колебаний струны

В силу симметрии задачи уравнение (1) достаточно рассмотреть в области , при этом можно считать выполненным условие:

Решение  будем искать ограниченным при  и при . Применяем преобразование Лапласа по переменной  к (1):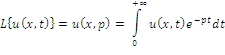                          

В результате, действуя аналогично (2) с учетом начальных условий и (3) в точкеполучаем операторное уравнение:

где обозначено  (главное значение корня при p>0), , .

Из уравнения (5), используя условие (3) (соответствующее условию «склейки» при x=0) однозначно находим образ искомого решения u(x,t):

где  .

Найдем асимптотику при больших , Rep>0 интегралов из (6). В данном случае асимптотика проще вычисляется непосредственно из вида интегралов (5) интегрированием по частям и соответствующим оценкам согласно общей методике построения асимптотического ряда [2]. В результате достаточно громоздких вычислений можно убедиться, что, например главный асимптотический член первого слагаемого имеет вид:

(здесь точка максимального вклада для интеграла x=0)

Далее исследуется асимптотика двух оставшихся слагаемых из (6):u₂и u₃, которая оказывается аналогичной приведенной выше. Точки максимально вклада интеграла здесь соответственно левый и правый концы промежутка интегрирования:

,

.

Отметим, что из приведенных асимптотических формул вытекает, что величина в правой части формулы (6) является образом и, следовательно, найдется функция  действительно являющаяся решением задачи (1—4).

Записывая формулу обращения для первого слагаемого в (6):

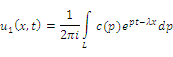
отметим, что вклад в величину  части внутреннего интеграла, а именно:

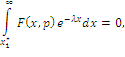
где  - первый положительный корень уравнения:

После этого допустимо поменять порядок интегрирования и затем остается воспользоваться известными формулами операционного исчисления.

Действительно пусть

где  и вертикальная прямая  принадлежит правой полуплоскости. Поскольку начало интегрирования  является точкой максимального вклада для внутреннего интеграла, то подынтегральная функция  внешнего интеграла имеет асимптотику:

где  не зависит от и на основании леммы Жордана.

Заметим, что если , т. е. решениев этом случае умножается на единичную функцию Хевисайда: .

На основании выше сказанного, первое слагаемое (6) перепишется в виде:

Известна формула:

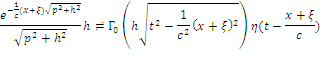
где  — функция Бесселя.

Согласно теореме запаздывания получим:

или окончательно:

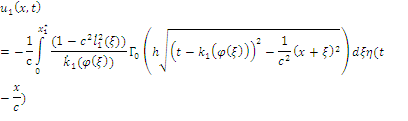
Аналогично обращаются два оставшиеся слагаемые в (6).

Окончательно можно записать:

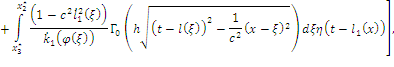
где

Закон движения плоского тела

На основании выше сказанного можем записать уравнение движения идеально — гладкогодиска радиуса и массы (рис. 1)

где  — уравнение границы тела:

-координата движущейся точки контакта,

Или в рассматриваемом случае из (1) получаем следующее нелинейное дифференциальное уравнение

где

Обратим внимание, что при рассматриваемом взаимодействии, как следует из последнего слагаемого (2), сила реакции стремится к бесконечности при Уравнение (2) легко решается в квадратурах. (3 вложенные квадратуры). Действительно, понижаем порядок (, получаем дифференциальное уравнение Бернулли

Из последнего уравнения находим

где

где  — пока произвольная постоянная.

Для проведения в дальнейшем анализа, в том числе и численного, закона движения  , далее проводятся преобразования формулы для , которые из-за громоздкости выражений не приводятся.

В результате с учётом начальных условий получаем

где обозначено

 — известные интегральные показательные функции, определяемые формулами:

Окончательно записываем закон движения тела (в виде обратной функции):

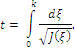
Список литературы:

1.Андрианов В.Л., Крысов С.В. Решение одной краевой задачи динамики упругой системы с движущейся нагрузкой методом интегральных преобразований // Дифференциальные и интегральные уравнения: Межвуз, тематич. сб. науч. тр. / Под редакцией Н.Ф Федорова. Горьк. гос. ун-т. Горький, 1985. С. 88—95.

2.Владимиров В.С. Уравнения математической физики. М.: Наука, 1967

3.Гахов Ф.Д. Краевые задачи. М.: Наука, 1977.

4.Григорян С.С., Григорян Д.М. Об ударе конусом по тонкой упругой мембране. ПММ, 1966, т. 30, вып. 6.

5.Диткин В.А., Прудников А.П. Операционное исчисление. М.: Высш. школа, 1975, С. 266—267.

6.Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного. М.: Наука, 1973.

7.Ленский Э.В. Удар клином по упругой нити. Инж. ж. МТТ, 1968, № 2.

8.Рахматулин Х.А., Демьянов Ю.А. Прочность при интенсивных кратковременных нагрузках. М.: АФизматгиз, 1961

9.Рябис А.А. поперечный удар притупленным телом по гибкой связи при наличии трения. Вестн. МГУ, сер.матем. механ., 1966, № 6.