ОБ ОДНОМ ПОДХОДЕ К ФОРМАЛИЗАЦИИ ОПЕРАЦИИ СТРУКТУРИЗАЦИИ, ПРОЦЕДУРНЫХ ПРЕОБРАЗОВАНИЙ И Т-ПРЕДСТАВЛЕНИЙ В ДЕСКРИПТИВНЫХ АЛГЕБРАХ ИЗОБРАЖЕНИЙ

Исхаков Алмаз Раилевич

преподаватель каф. «Информационных и полиграфических систем и технологий», ФГБОУ ВПО Башкирский государственный педагогический университет им. М. Акмуллы

Исламов Фаузиль Фаритович

студент Института профессионального образования и информационных технологий, ФГБОУ ВПО Башкирский государственный педагогический университет им. М. Акмуллы

Логвин Григорий Васильевич

студент Института профессионального образования и информационных технологий, ФГБОУ ВПО Башкирский государственный педагогический университет им. М. Акмуллы

Агафонов Михаил Сергеевич

студент Института профессионального образования и информационных технологий, ФГБОУ ВПО Башкирский государственный педагогический университет им. М .Акмуллы, г. Уфа

E-mail: intellab@mail.ru

Автоматизация обработки, анализа, оценивания и понимания информации, представленной в виде изображений, является одной из актуальной и узловой проблемой теоретической информатики, искусственного интеллекта и теории распознавания образов. Разнообразие применяемых методов не заменяет необходимости иметь некоторую регулярную основу для систематизации и выбора адекватных методов анализа изображений, единообразного представления обрабатываемых данных (изображений), отвечающих требованиям стандартных алгоритмов распознавания к исходной информации, построения математических моделей изображений, ориентированных на задачи распознавания, и в целом - наличия некоторого универсального языка для единообразного описания изображений и преобразований над ними. В рамках указанной проблемы ведущим направлением стала «алгебраизация» обработки, анализа и распознавания изображений [3, с. 1-19], заключающаяся в разработке и исследовании различных алгебр изображений (АИ). Основной целью алгебраического подхода является построение теоретического аппарата, обеспечивающего представление изображений и преобразований над ними в виде алгебраических структур, позволяющих использовать в анализе и распознавании изображений математические методы [6, с. 518 - 541].

В области распознавания образов и анализа изображений выделяют следующие основные стадии «алгебраизации»: математическая морфология (Г. Матерон (Matheron), Ж. Серра (Serra) [1970-е]); алгебра алгоритмов (Ю.И. Журавлев [1970-е]); теория образов (У. Гренандер (Grenander) [1970-е]); теория категорий в области распознавания образов (М. Павел (Pavel) [1970-е]); АИ (Ж. Серра, С. Стернберг (Sternberg) [1980- е]); стандартная алгебра изображений (САИ) (Г. Риттер (Ritter) [1990-е]); дескриптивная алгебра изображений (ДАИ) (И. Гуревич [1990- е]); ДАИ1К (И. Гуревич, В. Яшина [2002 и далее]).

Разработанный к настоящему моменту времени математический аппарат ДАИ [6, c. 518 - 541] и ДАИ1К [5, с. 298 - 328] обладает рядом недостатков: неудобная терминология формальных обозначений, отсутствие конструктивности в описаниях методов и операций, обобщенное определение операции структуризации, слабая связь семантической и контекстной информации изображений и т. п. В данной статье предлагается формализованный подход к перечисленным проблемам, обеспечивающий удобное описание различных действий над изображениями и связывающее математические аппараты смежных областей в единый универсальный аппарат.

Реализации изображений в ДАИ

Пусть объектом наблюдения является совокупность объектов или процессов действительности, которую будем называть сценой наблюдения или просто сценой. Изображение сцены может быть задано в разных форматах, которые называются его реализациями [6, c. 518 – 541]. Таким образом, изображение  может быть задано в виде совокупности его реализаций , соответствующих бинарным, полутоновым и цветным (полноцветное или палитровое) изображениям:

1.            , где ;

2.            , где ;

3.            , где .

По умолчанию цветные реализации представляются в полноцветной форме.

Операция структуризации реализаций изображений в ДАИ

К числу операций, проводимых над реализациями изображений, относятся [6, c. 518 – 541]: операция структуризации ; процедурные преобразования  и параметрические преобразования ; Т-представления  и Р-представления . Далее будут приведены теоретические положения, полученные лично А.Р. Исхаковым в ходе исследований диссертационной работы для операции структуризации, процедурных преобразований и Т-представлений.

Согласно определению моделирования и смысла термина «структуризация», под действием структуризации нужно понимать процесс создания модели сцены в виде изображения, содержащего идеальные формы изображений реальных объектов на сцене. Предлагаются следующие варианты интерпретации операции структуризации : выделение на изображении структурных элементов или сложной структуры и восстановление идеальной формы структурных элементов или сложной структуры. Зафиксированные на изображении «идеальные» структурные элементы в дальнейшем будет удобно использовать в качестве совокупности фактов для системы распознавания посредством логического вывода. В данной работе операция структуризации рассматривается в виде действия ввода в реализацию изображения  некоторой структуры через фиксацию в нем структурных элементов. Таким образом, предлагаются следующие варианты интерпретации операции структуризации:

,

где , где  - конечное множество структурных элементов, обычно представляемых геометрическими фигурами на плоскости. Запись  означает ввод структурного признака  в исходное изображение  и получение после этого действия изображения . Отдельно можно выделить еще одну форму этой операции:

,

где  - есть пустой структурный элемент множества .

Определенная таким образом операция структуризации обладает важными свойствами для линейной последовательности и иерархической взаимосвязи структурных элементов.

Основное свойство операции структуризации для линейного представления:

Дополнительное свойство структуризации для древовидного представления :

, где

 есть дерево, заданное множествами вершин  и дуг , а  - множество, получаемое из множества  исключением корня, узлов и повторяющихся листочков.

Процедурные преобразования в ДАИ

Преобразования изображений представляет единственный инструмент преобразования данных одного вида в другой или в тот же самый. Процедурное преобразование согласно определению в себя включает такие распространенные действия над изображением (или группой изображений), как конвертирование из одного формата в другое, фильтрацию шумов в изображении, определение краев и т. п. Таким образом, большинство алгоритмов обработки изображений относятся к группе процедурных преобразований.

Операция конвертации или конвертирования позволяет изменять форму реализации. Современные инструментальные средства позволяют конвертировать полутоновое изображение в бинарное изображение и цветное изображение в полутоновое изображение (или наоборот) [4, с. 517]. Предлагаемый подход обладает рядом преимуществ: ясна природа операции конвертирования, конструктивность определения операции, прозрачность в применении операции, совместимость с другими видами операциями. Операции конвертирования формализовано можно записать следующим образом:

1.  пороговое конвертирование полутоновой реализации в бинарную реализацию с порогом :

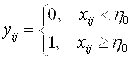, где  и , т.е.  или .

2.  конвертирование цветной реализации (полноцветное изображение) в полутоновую реализацию:

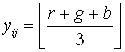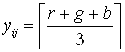, где  или  и , т.е.  или .

3.  комплексная операция конвертирования цветной реализации (полноцветное изображение) в бинарное бинарную реализацию с отсечением по порогу :

Следовательно,

,

где , т.е. .

Аналогичным образом можно записывать и процедурные преобразования, использующие операции пространственных линейных и нелинейных фильтраций [1, с. 131; 2, с. 103; 4, с. 532]. Пусть задана полутоновая реализация  размера . Рассмотрим линейные и нелинейные пространственные фильтры и маску размера , где  и a и b – суть неотрицательные целые числа. Отклик в точке  для реализации  обозначим . В таком случае он будет определен как , где  - маска размера , .

Ясно, что отклик  используется для вычисления яркости в точке с координатами . Если же отклик за область определений полутоновой реализации, то применяется техническая операция отсечения. В таком случае уместно будет сказать, что отклик вычисляется с точностью до остатка, т. е.

Тогда процедурное преобразование с операцией фильтрации запишется следующим образом:

, где

1.            для общего случая фильтрации

2.            для однородного усредняющего фильтра

3.            для сглаживающего фильтра с взвешенным средним

4.            для фильтров, основанных на порядковых статистиках (медианный)

, где

 - алгоритм сортировки по неубыванию

5.            для фильтра повышения резкости с использованием лапласиана

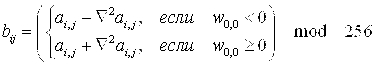
6.            для фильтрации с нерезким маскированием

, где

 - исходное изображение, а  - расфокусированное изображение

7.            для фильтрации с подъемом высоких частот

, где

Следующей разновидностью процедурных преобразований являются методы математической морфологии [1, с. 747; 2, с. 351; 4, с. 571]. В данной работе роль базовых морфологических операций играют операции дилатации и эрозии.

Определение [2, с. 354]: Дилатацией множества A по множеству B называется множество

Определение [2, с. 354]: Эрозией множеств A и B называется множество .

Используем для операции дилатации обозначение , а для операции эрозии – обозначение , где , .

Аналогично можно определить операции замыкания и размыкания [2, с. 354]:

 и

В ходе исследований было сформулировано и доказано утверждение.

Утверждение (об эквивалентности логических и алгебраических операций): Для процедурных преобразований бинарных реализаций на базе морфологических операций дилатации и эрозии выполняются следующие равенства:

,

где .

Доказательство: Эти равенства будут выполнены, если маски левых и правых частей равенства будут совпадать, т. е.

, для любых  и

Итак, рассмотрим первое равенство. Для левой части этого равенства верно

,

где 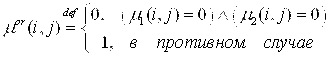    (1)

Для правой части этого равенства верно ,

где 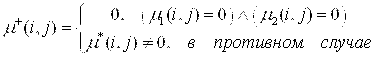  (2)

При определении операций, как в (1) и (2) верно неравенство . Это означает, что, если определить (2) как

   (3),

то будет выполняться равенство  для любых  и .

Аналогично можно доказать второе равенство:

Пусть маски определены следующим образом:

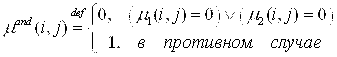(4)

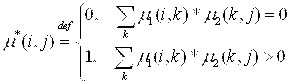и        (5)

Равенство  нужно рассматривать для двух случаев, в силу сложности самих операций. Пусть, для первого случая ,

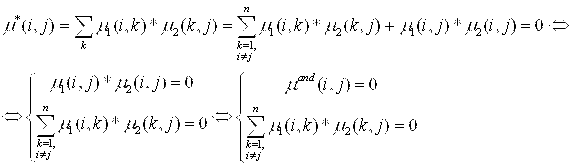
Следовательно, так как , то  и .

Если же , то согласно (5)  и

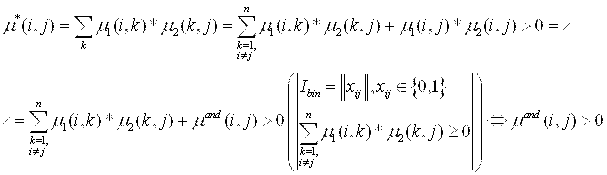, т.е.

, в силу того, что .

Т-представления в ДАИ

Представление изображения применяется при создании формальной схемы, предназначенной для получения описания изображения сцены в терминах структурных элементов. В алгебраическом подходе к анализу и обработке изображений И.Б. Гуревича определяются Т-, Р- и G-представления [6, с. 518 - 541]. T-представления позволяют решать задачи обработки и преобразования изображений. Сформулируем математические модели Т-представлений для рассмотренных выше процедурных преобразований.

Обобщенная математическая модель Т-представления с операциями порогового конвертирования с произвольной реализации  в бинарную реализацию  с последующей фиксацией структурных элементов  будет иметь вид:

,

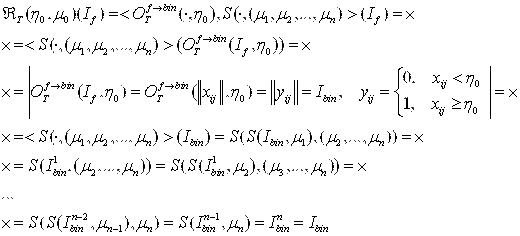где .

Математическая модель Т-представления с операциями пространственной фильтрации с ядром ранга  и структуризацией элементов  имеет вид:

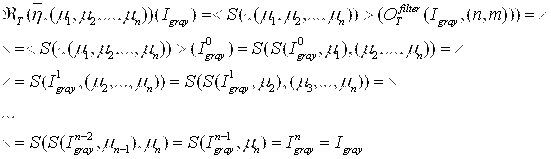
Аналогичным образом можно записать и математическую модель Т-представления с использованием операций математической морфологии. Например, математическую модель Т-представления с морфологической операцией размыкания и операцией структуризации последовательности элементов  в бинарной реализации  имеет вид:

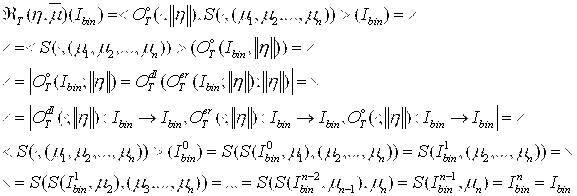
Заключение

В данной статье приведены теоретические положения, полученные А.Р. Исхаковым в ходе исследований по диссертационной работе. В число основных результатов, описанных в статье, входят: формализованное определение операции структуризации с ее основным и дополнительным свойствами, математические модели процедурных преобразований на основе операции конвертирования, линейной и нелинейной операций фильтрации, морфологических операций дилатации, эрозии, замыкания и размыкания. Для морфологических операций сформулировано и доказано утверждение «об эквивалентности логических и алгебраических операций». Эти результаты имеют важное значение для развития и обобщения алгебраического подхода к обработке, анализу и распознаванию изображений.

Список литературы

1. Гонсалес Р., Вудс Р. Цифровая обработка изображений, 2005

2. Гонсалес Р., Вудс Р., Эддинс С. Цифровая обработка изображений в среде Matlab. М.: Техносфера, 2006

3.Гуревич И.Б., Журавлев Ю.И., Сметанин Ю.Г. Дескриптивные алгебры изображений: определения и примеры // Автометрия.-1999.-No.6.-С. 1 -19.

4.  Дьяконов В., Абраменкова И. Matlab: обработка сигналов и изображений, 2002

5. I.B. Gurevich, V.V. Yashina. Operations of Descriptive Image Algebras with One Ring // Pattern Recognition and Image Analysis: Advances in Mathematical Theory and Applications. Pleiades Publishing, Inc. 2006. – Vol.16,No. 3.-pp. 298-328.

6. I.B. Gurevich and V.V. Yashina. Descriptive Approach to Image Analysis: Image Models // Pattern Recognition and Image Analysis: Advances in Mathematical Theory and Applications. – MAIK "Nauka/Interperiodica"/Pleiades Publishing, Inc., 2008. - Vol.18, No.4. - P. 518-541.