Статья опубликована в рамках: LI Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 30 ноября 2015 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции, Сборник статей конференции часть II
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
УПРАВЛЕНИЕ И МОДЕЛИРОВАНИЕ СЛУЧАЙНОГО ДВИЖЕНИЯ КОСМИЧЕСКОГО АППАРАТА В ОКРЕСТНОСТИ РЕЗОНАНСА ПРИ СПУСКЕ В АТМОСФЕРЕ ВЕНЕРЫ
Любимов Владислав Васильевич
д-р техн. наук, доцент, заведующий кафедрой высшей математики, Самарский Государственный Аэрокосмический Университет, РФ, г. Самара
E-mail: vlubimov@mail.ru
Лашин Вячеслав Сергеевич
аспирант, Самарский Государственный Аэрокосмический Университет, РФ, г. Самара
CONTROL AND SIMULATION OF A RANDOM MOTION OF THE SPACECRAFT IN THE VICINITY OF THE RESONANCE AT THE DESCENT IN VENUS ATMOSPHERE
Vladislav Lyubimov
associate professor, doctor of technical sciences, Head of the Chair of Higher Mathematics, Samara State Aerospace University, Russia, Samara
Vyacheslav Lashin
postgraduate student, Samara State Aerospace University,
Russia, Samara
АННОТАЦИЯ
Рассматривается спуск космического аппарата с малой инерционной и аэродинамической асимметрией в атмосфере Венеры. Исследуется случайный характер вращательного движения космического аппарата в окрестности главного резонанса при малых углах атаки. Показывается, что применение двух разных законов управления величиной инерционной асимметрии обеспечивает гарантированный проход через резонанс. Приводится условие гарантированного прохода через резонанс.
ABSTRACT
We consider the descent of the spacecraft with a small inertial and aerodynamic asymmetry in the atmosphere of Venus. We study the random nature of the rotational motion of the spacecraft in the vicinity of the main resonance at small angles of attack. Recorded the condition of the guaranteed passage through resonance. It is shown that the application of the two different laws control the amount of inertial asymmetry provides a guaranteed passage through resonance.
Ключевые слова: твердое тело; космический аппарат; атмосфера; резонанс; вероятность захвата; асимметрия; угловая скорость; угол атаки.
Keywords: solid; spacecraft; atmosphere; resonance; probability of capture; asymmetry; angular velocity; angle of attack.
При отделении от базового космического аппарата спускаемому аппарату передается небольшое значение кинетического момента [1]. Это приводит к появлению малой начальной угловой скорости, которую имеет спускаемый аппарат при входе в плотные слои атмосферы. Известно, что наличие асимметрии у спускаемого аппарата может привести к реализации различных резонансных явлений, способных явиться причиной различных аварийных ситуаций. Кроме непосредственно длительных резонансов моменты от асимметрии могут быть причиной аварийных ситуаций, вызванных реализацией вторичных резонансных эффектов [2–4].
Начальные условия движения на сепаратрисе, отделяющей область вращения от области резонансных колебаний, расположены случайным образом. В связи с этим возникает задача о нахождении вероятности захвата системы в резонансную область [5].
Рассмотрим движение космического аппарата в атмосфере Венеры как твердого тела конической формы с малой инерционной и аэродинамической асимметриями при малых углах атаки. Квазилинейная система уравнений движения асимметричного космического аппарата относительно центра масс, полученная посредством известного подхода [6], имеет вид:
 , (1)
, (1)
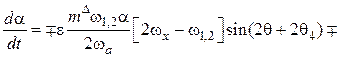
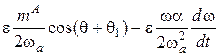 , (2)
, (2)
![]()

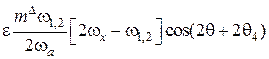 , (3)
, (3)
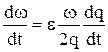 . (4)
. (4)
Здесь q=j-p/2, ![]() - угловая скорость тела относительно связанной с телом оси X, α – угол атаки, j-угол аэродинамического крена, w-известная функция переменных движения центра масс,
- угловая скорость тела относительно связанной с телом оси X, α – угол атаки, j-угол аэродинамического крена, w-известная функция переменных движения центра масс, ![]() ,
, ![]() ,
, 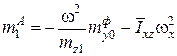 ,
, 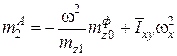 ;
;![]() ,
, ![]() ,
, ![]() ,
, ![]() – коэффициенты аэродинамической асимметрии формы, лобового сопротивления и восстанавливающего момента.
– коэффициенты аэродинамической асимметрии формы, лобового сопротивления и восстанавливающего момента.
При малых величинах момента a и малых углах атаки можно получить выражение для оценки вероятности захвата [7]:
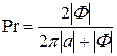 . (5)
. (5)
Здесь 
где
 ,
,  .
.
Выражение (5) рассматривается при выполнении неравенства ![]() .
.
В итоге получаем, что величина параметра асимметрии ![]() при вероятности захвата равной нулю (гарантированный проход через резонанс) определяется следующим образом:
при вероятности захвата равной нулю (гарантированный проход через резонанс) определяется следующим образом:
 . (6)
. (6)
Здесь величины ![]() вычисляются на сепаратрисе [7].
вычисляются на сепаратрисе [7].
С целью уменьшения величины вероятности захвата в резонанс введем в рассмотрение экспоненциальный и синусоидальный законы уменьшения инерционной асимметрии:
![]() , (7)
, (7)
![]() . (8)
. (8)
Здесь k и ![]() – коэффициенты управления, Н- высота полета аппарата.
– коэффициенты управления, Н- высота полета аппарата.
При атмосферном спуске наблюдается уменьшение высоты полёта H. В результате осуществляется уменьшение параметра инерционной асимметрии ![]()
При численном моделировании предполагалось, что космический аппарат конической формы с массой 10 кг и малой асимметрией совершает спуск в атмосфере Венеры при малых углах атаки. Значения коэффициентов управления были следующими: k=0.029, ![]() =
=![]() и k=0.3,
и k=0.3, ![]() =10-6 (для экспоненциального и синусоидального законов управления, соответственно).
=10-6 (для экспоненциального и синусоидального законов управления, соответственно).
Часть результатов численного моделирования для экспоненциального закона представлена на рисунках 1–3. На рисунке 1 содержатся: изменение угловой скорости ![]() (t) и её резонансных значений
(t) и её резонансных значений ![]() (t) (кривая, пропорциональная изменению скоростного напора q(t)). Параметры управления выбраны таким образом, что показанное на рис. 1 изменение угловой скорости
(t) (кривая, пропорциональная изменению скоростного напора q(t)). Параметры управления выбраны таким образом, что показанное на рис. 1 изменение угловой скорости ![]() (t) и резонансного значения данной угловой скорости
(t) и резонансного значения данной угловой скорости ![]() (t)
(t)
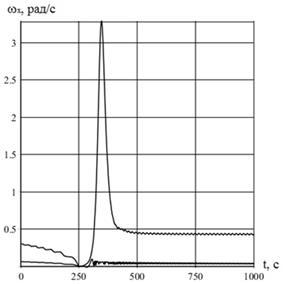
Рисунок 1. Эволюция угловой скорости ![]() и резонансного значения
и резонансного значения

Рисунок 2. изменение параметра по экспоненциальному закону
характерно как для экспоненциального, так и для синусоидального закона изменения ![]() . На рисунке 1 показано, что при уменьшении инерционной асимметрии (в соответствии с законом (7)) на восходящей ветви скоростного напора происходит реализация прохода через резонанс. Проход через резонанс
. На рисунке 1 показано, что при уменьшении инерционной асимметрии (в соответствии с законом (7)) на восходящей ветви скоростного напора происходит реализация прохода через резонанс. Проход через резонанс

Рисунок 3. Вероятность захвата твердого тела в резонанс при экспоненциальном законе изменения
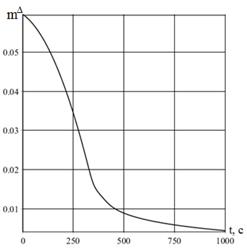
Рисунок 4. изменение параметра по синусоидальному закону
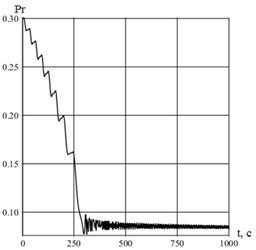
Рисунок 5. Вероятность захвата твердого тела в резонанс при синусоидальном законе изменения
имеет место на 250 секунде полета в атмосфере. Дальнейшее уменьшение параметра асимметрии ![]() приводит к стабилизации угловой скорости и угла атаки. На рисунке 2 представлен результат изменения инерционной асимметрии
приводит к стабилизации угловой скорости и угла атаки. На рисунке 2 представлен результат изменения инерционной асимметрии ![]() в соответствии с экспоненциальным законом (7). На рисунке 3 показано, что уменьшение инерционной асиметрии способствует также уменьшению вероятности захвата. При достижении резонансных значений угловой скорости (250 с.) вероятность захвата равна малой величине (менее 0,15). На рисунках 4–5 представлены: уменьшение инерционной асимметрии и расчет вероятности захвата, соответственно. При этом, в качестве закона управления асимметрией использовался синусоидальный закон (8). Численное моделирование случайного движения космического аппарата в окрестности резонанса позволяет сделать вывод о том, что выбор коэффициентов в законах управления (7) и (8) позволяет обеспечить гарантированный проход через резонанс. Из сравнения результатов численного моделирования, представленных на рисунках 2 и 4 следует, что синусоидальный закон управления (по сравнению с экспоненциальным законом) позволяет достигнуть меньших величин инерционной асимметрии. Величины вероятности захвата в резонанс при достижении резонансных значений угловой скорости на рисунках 3 и 5 также несколько меньше при синусоидальном законе, чем при экспоненциальном законе. Следовательно, выбирая один из законов управления величиной инерционной асимметрии (7) или (8) можно уменьшить вероятность захвата системы в резонанс до величины, обеспечивающей гарантированный проход системы уравнений движения через резонанс (6).
в соответствии с экспоненциальным законом (7). На рисунке 3 показано, что уменьшение инерционной асиметрии способствует также уменьшению вероятности захвата. При достижении резонансных значений угловой скорости (250 с.) вероятность захвата равна малой величине (менее 0,15). На рисунках 4–5 представлены: уменьшение инерционной асимметрии и расчет вероятности захвата, соответственно. При этом, в качестве закона управления асимметрией использовался синусоидальный закон (8). Численное моделирование случайного движения космического аппарата в окрестности резонанса позволяет сделать вывод о том, что выбор коэффициентов в законах управления (7) и (8) позволяет обеспечить гарантированный проход через резонанс. Из сравнения результатов численного моделирования, представленных на рисунках 2 и 4 следует, что синусоидальный закон управления (по сравнению с экспоненциальным законом) позволяет достигнуть меньших величин инерционной асимметрии. Величины вероятности захвата в резонанс при достижении резонансных значений угловой скорости на рисунках 3 и 5 также несколько меньше при синусоидальном законе, чем при экспоненциальном законе. Следовательно, выбирая один из законов управления величиной инерционной асимметрии (7) или (8) можно уменьшить вероятность захвата системы в резонанс до величины, обеспечивающей гарантированный проход системы уравнений движения через резонанс (6).
Результаты работы представляют определенный практический интерес, так как в рассмотренной системе малое уменьшение величины инерционной асимметрии позволяет обеспечить реализацию нерезонансного вращения космического аппарата. Представленная работа относиться к классу задач, в которых изучается управление в системах с динамическим хаосом [8].
Список литературы:
- Калаев М.П., Любимов В.В., Сёмкин Н.Д. Полунатурное и имитационное моделирование процесса отделения микроспутника // Гироскопия и навигация. – 2014. – № 2 (85). – С. 52–60.
- Любимов В.В. Асимптотический анализ вторичных резонансных эффектов при вращении космического аппарата с малой асимметрией в атмосфере // Известия вузов. Авиационная техника. – 2014. – № 3. – С. 23–28.
- Любимов В.В., Лашин В.С., Численное моделирование резонансного эффекта с изменением направления вращения при атмосферном спуске асимметричного наноспутника // Информационные технологии и нанотехнологии (ИТНТ-2015): материалы международной конференции и молодежной школы. – Самара, 2015. – С. 250–253.
- Заболотнов Ю.М., Любимов В.В. Вторичный резонансный эффект при движении КА в атмосфере // Космические исследования. – 1998. – Т. 36. – № 2. – С. 206–214.
- Нейштадт А.И. Захват в резонанс и рассеяние на резонансах в двухчастотных системах // Тр. МИАН. – 2005. – Т. 250. – C. 198–218.
- Заболотнов Ю.М. Асимптотический анализ квазилинейных уравнений движений в атмосфере КА с малой асимметрией III. Космические исследования// – 1994. – Т. 32. – № 4–5. – C. 112–125.
- Любимов В.В. Оценка вероятности захвата в резонанс при движении динамически несимметричного твердого тела // Вестник СамГТУ. Серия: Физико-математические науки. – 2007. – № 2. (15) – С. 110–115.
- Магницкий Н.А., Сидоров С.В. Новые методы хаотической динамики. – М.: Едиториал УРСС, 2004. – 320 с.
дипломов


Оставить комментарий