СТРУКТУРНАЯ  САМООРГАНИЗАЦИИ  ПРИ  МОЛЕКУЛЯРНО-ДИНАМИЧЕСКОМ  СТЕКЛОВАНИИ  СПЛАВА  СИСТЕМЫ  Fe-P

Дейч  Денис  Борисович

старший  преподаватель  ВГТУ,  г.  Воронеж

E-mail: 

В  настоящей  работе  модельные  представления  о  структуре  моноатомных  металлических  стекол,  изложенные  в  работах  [1;  2]  были  развиты  и  обобщены  на  случай  двухкомпонетных  аморфных  систем  типа  металл-металлоид  на  примере  сплава  Fe₈₃P₁₇. 

Молекулярно-динамическая  модель  расплава  Fe₈₃P₁₇,  содержащая  100000  атомов  (83000  атомов  Fe  и  17000  атомов  P)  была  построена  при  T=2300  K  с  плотностью  7180  кг/м³  (величина  плотности  взята  из  работы  [3]).  Исходная  структура  представляла  собой  случайную  плотную  упаковку  атомов.

Взаимодействие  пар  Fe-Fe  описывали  с  помощью  эмпирического  парного  потенциала  Пака-Доямы  [4].  Для  пар  Fe-P  был  выбран  эмпирический  парный  потенциал,  предложенный  Джонсоном,  Динсом  и  Дамаском  для  описания  взаимодействия  пар  Fe-C  [5]  с  модифицированными  параметрами.  Согласно  имеющимся  в  литературе  данным  по  экспериментальному  исследованию  термодинамических  свойств  расплавов  системы  Fe-P  тенденция  к  объединению  атомов  фосфора  в  жидкости  отсутствует.  Чтобы  исключить  контакт  этих  пар  на  малых  расстояниях  для  описания  их  взаимодействия  был  выбран  чисто  отталкивательный  потенциал  Борна-Майера  [4]. 

Методика  молекулярно-динамического  расчета  состояла  в  численном  интегрировании  уравнений  движения  с  временным  шагом  Δt=1.523×10^-15с  по  алгоритму  Верле  [6].  Система  в  изохорических  условиях  охлаждалась  со  скоростью  4.4´10¹²  К/с 

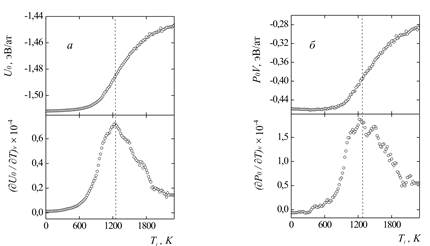
Как  видно  из  рис.  1,  в  процессе  охлаждения  на  температурных  зависимостях  U₀  и  P₀V  вблизи  температуры  1220  K  наблюдается  точка  перегиба,  о  чем  свидетельствуют  максимумы  первых  производных  от  указанных  термодинамических  величин. 

Рисунок  1.  Зависимость  термодинамических  функций  модели  после  статической  релаксации  и  их  производных  от  температуры  «окружающей  среды»  T_i  в  условиях  охлаждения  расплава  со  скоростью  4.4×10¹²  K/с:  (а)-потенциальная  энергия,  (б)-  произведение  давления  на  объем.

На  основе  статистико-геометрического  анализа  путем  построения  многогранников  Вороного  (МВ)  было  установлено  распределение  координационных  многогранников  модели  аморфного  сплава  Fe₈₃P₁₇.  Напомним,  что  отдельный  МВ  можно  описать  совокупностью  чисел  n_q,  равных  числу  граней,  имеющих  q  сторон  (n₃-n₄-n₅-…). 

Рисунок  2.  Основные  координационные  многогранники  системы  Fe-P:  (а)  -  икосаэдр  (б)  –  антипризма  Архимеда,  накрытая  двумя  полуоктаэдрами;  (в)  –  одиннадцативершинник

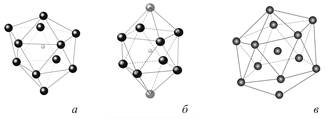
В  распределении  по  типу  МВ,  построенных  на  атомах  фосфора  в  модели  аморфного  сплава  Fe₈₃P₁₇,  самым  распространенным  является  МВ  (0-2-8-1)  (25,18%)  (рис.  2а).  Соответствующий  этому  МВ  координационный  многогранник  можно  получить  из  антипризмы  Архимеда  (рис.  2б),  накрытой  двумя  полуоктаэдрами,  путем  добавления  одного  атома,  или  из  икосаэдра  -  путем  удалении  одного  атома  (рис.2в).

В  соответствии  с  изложенными  в  [1;  2]  представлениями  о  структуре  чистых  металлических  стекол  определяющую  роль  в  стабилизации  аморфного  состояния  в  процессе  закалки  играет  увеличение  доли  икосаэдров,  имеющих  минимальный  свободный  объем  из  всех  координационных  многогранников  железа  и  в  то  же  время  несовместимых  с  трансляционной  симметрией. 

В  настоящей  работе  в  результате  статистико-геометрического  анализа  на  основе  построения  полиэдров  Вороного  для  модели  аморфного  сплава  Fe₈₃P₁₇  было  установлено,  что  основными  структурными  единицами,  стабилизирующими  аморфную  фазу,  являются  икосаэдр  (0-0-12-0)  -  преимущественно  с  атомом  железа  в  центре  и  одиннадцативершинник  (0-2-8-1)  с  атомом  фосфора  в  центре.  Под  стабилизацией  аморфной  фазы  мы  подразумеваем  существенное  уменьшение  свободного  объема  системы,  за  счет  значительного  увеличения  доли  компактных  и  энергетически  выгодных  координационных  многогранников  (0-0-12-0)  и  (0-2-8-1),  которые  несовместимы  с  трансляционной  симметрией  термодинамически  равновесных  фаз. 

Для  изучения  закономерностей  структурной  организации  таких  координационных  многогранников  при  охлаждении  модели  расплава  Fe₈₃P₁₇  в  рамках  теории  протекания  был  проведен  кластерный  анализ.  Первые  три  максимума  на  функции  радиального  распределения  атомов  g_II(r)  (рис  4а.),  находящихся  в  центрах  МВ  (0-0-12-0)  и  (0-2-8-1),  соответствуют  взаимопроникающим  контактам  (первый  максимум),  контакту  по  граням  и  ребрам  (второй  максимум)  и  контакту  по  вершинам  (третий  максимум)  рассматриваемых  координационных  многогранников.

На  рисунке  4б  приведены  зависимости  размера  наибольшего  кластера,  состоящего  из  атомов,  находящихся  в  центрах  координационных  многогранников  типа  (0-2-8-1)  и  (0-0-12-0),  с  расстояниями  между  соседями  меньшими,  либо  равными  r,  от  величины  r  при  температурах  «окружающей  среды»  2300,  1600,  1400,  1200,  1100  и  0  K.  Как  видно  на  рисунке  4б,  при  T_i>1200  K  порог  перколяции  наблюдается  правее  штриховой  вертикальной  линии,  разделяющей  область  взаимопроникающих  и  контактирующих  между  собой  координационных  многогранников  от  области  изолированных  координационных  многогранников. 

Рисунок  3.  Парная  функция  радиального  распределения  g_II(r)  атомов  (T=1150  K),  находящихся  в  центрах  координационных  многогранников  типа  0-0-12-0  и  0-2-8-1  -  а  и  число  N_I^max  таких  атомов  в  наибольшем  по  размеру  кластере  с  расстояниями  между  соседями  меньшими,  либо  равными  r-б.  Штриховая  вертикальная  линия  (r=5,19Å)  разделяет  области  взаимопроникающих  и  контактирующих  между  собой  (слева)  и  изолированных  (справа)  координационных  многогранников.  Цифры  1,  2,  3,  4,  5  и  6  соответствуют  температурам  «окружающей  среды»  2300,  1500,  1300,  1200,  1000  и  0  K.

При  охлаждении  ниже  1200  K  порог  перколяции  смещается  левее  штриховой  вертикальной  линии,  при  этом  происходит  образование  и  последующий  рост  пронизывающего  всю  структуру  перколяционного  кластера  из  взаимопроникающих  и  контактирующих  между  собой  рассматриваемых  координационных  многогранников.

Выявленные  закономерности  структурной  самоорганизации  в  аморфном  сплаве  Fe₈₃P₁₇  при  стекловании  хорошо  коррелируют  с  температурными  зависимостями  основных  термодинамических  характеристик  модели  (рис.  1),  которые  обнаруживают  при  T=1200  K  некоторые  признаки  фазового  перехода  второго  рода  и  объясняют  их  поведение  на  микроскопическом  уровне. 

Список  литературы:

1.Евтеев  А.  В.,  Косилов  А.  Т.,  Левченко  Е.  В.  Структурная  модель  стеклования  чистых  металлов  //  Письма  в  ЖЭТФ.  2002.  т.  76.  №  5.  С.  115-117.

2.Евтеев  А.  В.,  Косилов  А.  Т.,  Левченко  Е.  В.,  Прядильщиков  А.  Ю.  Молекулярно-динамическое  изучение  процесса  стеклования  бинарного  сплава  Ni₆₀Ag₄₀  //  ЖЭТФ.  2007.  т.132.  №  6.  С.  1352-1358.

3.Островский  О.  И.,  Григорян  В.  А.,  Вишкарев  А.  Ф.  Свойства  металлических  расплавов.  М.:  Металлургия,  1988.-  304  с.

4.Torrens  I.  M.  Interatomic  Potentials.  -  N.  Y.:  Acad.  Press,  1972.  –  205  p.

5.Johnson  R.  A.,  Dienes  G.  J.,  Damask  A.  C.  Calculations  of  the  Energy  and  Migration  Characteristics  of  Carbon  and  Nitrogen  in  a-Iron  and  Vanadium  //  Acta  Met.  –  1964.  Vol.  12.  –  №  11.  –  P.  1215-1224.

6.Verlet  L.  Computer  Experiments  on  Classical  Fluids.  I.  Thermodynamic  Properties  of  Lennard-Jones  Molecules  //  Phys.  Rev.  1967.  Vol.  159.  P.  98-103.