Статья опубликована в рамках: XLIII Международной научно-практической конференции «Экономика и современный менеджмент: теория и практика» (Россия, г. Новосибирск, 05 ноября 2014 г.)
Наука: Экономика
Секция: Теория управления экономическими системами
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
РЕШЕНИЕ ЭКОНОМИЧЕСКИХ ЗАДАЧ С ПОМОЩЬЮ МАТРИЧНОГО МЕТОДА
Григорьева Диана Рамилевна
доцент кафедры «Математические методы в экономике» «Казанский (Приволжский) федеральный университет», РФ, г. Набережные Челны
Герасимов Владислав Олегович
студент кафедры «Экономическая теория и экономическая политика» «Казанский (Приволжский) федеральный университет», РФ, г. Набережные Челны
ECONOMIC CONSIDERATIONS OF USING MATRIX METHODS .
Grigoreva Diana
associate Professor of " Mathematical Methods in Economics" Kazan (Volga region) Federal University, Russia, NaberezhnyeChelny
Gerasimov Vladislav
student of the Department " Economic theory and economic policy" Kazan (Volga region) Federal University, Russia, Naberezhnye Chelny
АННОТАЦИЯ
В статье рассматривается вопрос о развитии современной экономики и математических методах в решении экономических задач, в частности матричным методом решения экономических задач, а также роль человека в вычислительных процессах.
ABSTRACT
In article the question of development of modern economy and mathematical methods in the solution of economic tasks, in particular by a matrix method of the solution of economic tasks, and also a role of the person in computing processes is considered.
Ключевые слова: экономика; матричный метод; матрица; математические методы; анализ.
Keywords: economy; matrix method; the matrix; mathematical methods; analysis.
На сегодняшний день известно большое количество разных мнений на процессы, которые происходят в обществе. И не важно, как разные политические силы смогут воспринятьтакие процессы, однако, ни одна из этих сил не сможет отрицать того, что современные экономические условия в нашей жизни стали намного сложнее. Принимать важные стратегические решения для общества и частных лиц стало труднее. Именно в моменты преодоления всех этих препятствий, появляется большой интерес к математическим методам, которые можно было бы применять в экономике, то есть к таким математическим методам, которые смогли бы выработать лучшую стратегию на решение действующих проблем и на долгосрочные проекты [1]. Таким видом выхода из сложившейся ситуации стало решение задач в экономике при помощи матричных методов. На внедрение и развитие математических методов в решении экономических задач, большое влияние оказало создание и развитие современной вычислительной техники. Вычислительная техника нового поколения позволила применять на практике множество новых методов, которые были описаны ранее только в теории или объяснялись на простых примерах. Но никакая вычислительная техника не способна заменить человека и поэтому, люди должны уметь эффективно использовать теоретические знания в области математики в экономики. В нашем же случае, уметь правильно решать экономические задачи при помощи матричных методов [4].
Матрица представляет
собой математический объект, который записывается в формате прямоугольной таблицы с элементами внутри. Над матрицами можно осуществлять следующие операции:
1. равенство матриц;
2. транспонирование;
3. сложение;
4. умножение матриц на число;
5. умножение одной матрицы на другую матрицу.
Матрица имеет следующий вид записи: A= 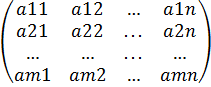 [2]/
[2]/
Матрицы начали появляться в середине восемнадцатого века в трудах английских математиков У.Р. Гамильтона и А. Кэли. Из русских ученых большой вклад в матричные операции внесли А.Н. Крылов и А.С. Лапло-Данилевский.
Сегодня любому квалифицированному экономисту просто необходима мощная математическая база. Для них, одним из главных предметов в высшей математике является линейная алгебра, а именно матричная алгебра. Это объясняется тем, что экономико-математические модели, которые часто применяются в исследовательских работах, не редко нужны для разъяснения различных взаимосвязанных экономических структур и их динамик во временных промежутках. Матричное отображение — один из наиболее компактных и удобных способов для решения многих экономических задач [3].
Обладая насыщенным экономическим содержанием, матричные методы все чаще применяются на практике: различные виды статистических расчётов, сокращение документооборота, организация внутри производства хозяйственных расчётов и экономико-математического анализа. Им пользуются при сравнении, при оценке структурных подразделений и работы самой организации в целом. Решая экономические задачи при помощи матричных методов, люди смогли решать основные задачи экономического типа на всех предприятиях и организациях [7].
Рассмотрим пример: Пусть фирма (Х) выпускает товары 3 видов (P1, P2, P3) и использует сырье 2 видов (S1, S2), нормальный расход будет равен:
А = 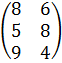 , С = (6070170). Стоимость единицы каждого вида сырья (денежных единиц) представлена матрицей: В =
, С = (6070170). Стоимость единицы каждого вида сырья (денежных единиц) представлена матрицей: В =![]() .
.
Решая данную задачу аналитическим способом мы получаем, что затраты первого сырья будут равны: ![]() = 8*60 + 5*70+9*170 = 2360 единиц;
= 8*60 + 5*70+9*170 = 2360 единиц;
Затраты второго сырья будут равны: ![]() = 6*60 + 8*70+4*170 = 1600 (единиц);
= 6*60 + 8*70+4*170 = 1600 (единиц);
Следовательно, матрица затрат сырья S может быть записана следующим способом: = С*А , где S — это затраты на сырье; С — это заказ; A — это матрица производства.
Тогда: S =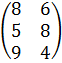 * (60 70170) = (2360 1600).
* (60 70170) = (2360 1600).
Общая стоимость сырья будет равна: Q= 2360*75+1600* 35= 233000.
Денежная единица может быть также записана и в матричном виде:
Q= S*B = (CA)B=(233000), где Q — общая стоимость; B — стоимостью единицы сырья; а S — затраты на сырье.
Использование матриц в экономике не может происходить без матриц Абеля. Именно они позволяютрассмотреть нужную отрасль компании и привести ее к критериям выбора правильной конкурентоспособности.
Рассмотрим пример:
Завоз определенных товаров на 1 склад можно представить следующей матрицей:![]() =
=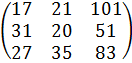 . Завоз товаров на 2 склад представить в виде матрицы:
. Завоз товаров на 2 склад представить в виде матрицы:![]() =
=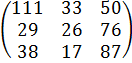 .
.
Нужно найти сумму завоза всех товаров; найти сумму годового завоза, если производится ежемесячный завоз идентичных партий товара.
Решение:
Найдём суммарный завоз:![]() +
+ ![]() =
= 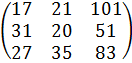 +
+ 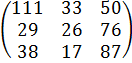 =
= 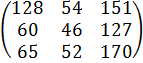
Найдём годовой завоз: 12*(![]() +
+ ![]() =
= 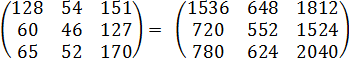
Ответ: 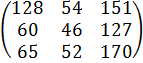 ,
,  . [5]
. [5]
Таким образом, матрицы можно эффективно использовать не только в науке, но и применять их на практике в крупных предприятиях для решения современных экономических задач. Матричный метод позволяет упростить работу человека, уменьшить количество критериев и альтернатив для выбора и получать выгодные варианты решения для выхода из различных экономических ситуаций. Также с помощью матричного метода человек получает готовый и обоснованный ответ в виде рейтинга альтернатив по всем критериям. Изучая матричный метод и чаще его практикуя в решении, можно добиться положительных результатов в кратчайшие сроки и поднять экономику на новый уровень [6].
Список литературы:
1.Басыров Р.Р., Григорьева Д.Р. The role, significance and influence of Information technologies on the economy. «Глобальный научный потенциал». СПб., — 2014 — № 7. — С. 61—63.
2.Высшая математика для экономистов: учебник / под ред. Н.Ш. Кремера. М.: ЮНИТИ-ДАНА, 2010.
3.Козак А.В., Пилиди В.С. Линейная алгебра. М.: Вузовская книга, 2005.
4.Кремер Н.Ш.; Путко Б.А.; Тришин И.М., «Математика для экономистов: от Арифметики до Эконометрики», М., 2007.
5.Морозова О.В., Долгополова А.Ф., Долгих Е.В. Экономико-математические методы: теория и практика. Ставрополь: СтГАУ «АГРУС», 2006.
6.Сирл С., Госман У. Матричная алгебра в экономике. М.: Статистика, 1974.
7.Шевцов Г.С. Линейная алгебра: теория и прикладные аспекты. М.: Финансы и статистика, 2003.
дипломов


Комментарии (1)
Оставить комментарий