МЕТОД СОСТАВЛЕНИЯ ОПТИМАЛЬНОГО ГРАФИКА РАБОТЫ ПЕРСОНАЛА

Богомольный Михаил Аркадьевич

канд. техн. наук, ГОУ ВПО КНИТУ — КАИ, доцент кафедры «Менеджмент», г. Казань

E-mail: bogomark@inbox.ru

Задача составления оптимального графика работы персонала решается менеджерами на предприятиях. Например, в [1, с. 267] приводитсяпримерсоставления графика работы обслуживающего персонала парка отдыха, наилучшего по критерию минимума общей суммы заработной платы сотрудников. В полученном решении видна недогрузка персонала, что приводит к лишним затратам организации.

Разберем упомянутый пример подробнее и далее будем именовать его базовым. В нем персонал формируется из сотрудников, работающих по пятидневной рабочей неделе с двумя днями отдыха подряд. Причем рассматривается семь видов графика рабочих и выходных дней обслуживающего персонала. У одних сотрудников днями отдыха являются суббота и воскресенье, у других — воскресенье и понедельник и так далее. Обозначим количество сотрудников, работающих по первому графику, через x₁, по второму — x₂и так далее. Переменные x_i, i= 1,2,…,7 образуют вектор x. Они должны удовлетворять требованиям  неотрицательности и целочисленности:

x_i ³0,       i = 1,2,…,7,                                              (1)

x_i   —  целые,    i = 1,2,…,7                                   (2)

На переменные накладываются также другие ог­раничения, которые требуют присутствия на рабочих местах такого количества служебного персонала, которое не меньше необходимого для нормального функционирования парка отдыха в конкретный день недели:

x^ТA^T³b^T.                                                                (3)

Здесь x^Т— вектор-строка искомых переменных, b^T— вектор-строка минимально необходимого количества сотрудников по дням недели, начиная с воскресенья и далее, A^T— матрица графиков работы сотрудников по дням недели. Приняты следующие значения:

b^T= ( 22  17  13  14  15  18  24 ) ,                                                  (4)

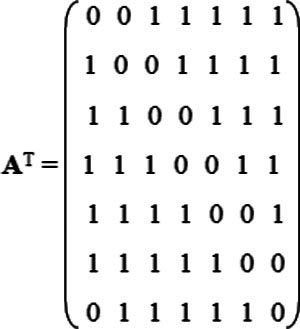                                                               (5)

Каждая строка в (5) соответствует определенному графику работы сотрудников по дням недели. Цифра 1 означает работу, 0 — отдых. Столбцы соответствуют последовательно воскресенью, понедельнику, вторнику и так далее. Последний столбец соответствует субботе. Значок Т означает операцию транспонирования.

За отработанный полный рабочий день каждый сотрудник получает 40 у.е. заработной платы. Критерий общей недельной суммы заработной платы сотрудников, работающих по пятидневному графику, имеет вид:

Z= 5*40*(x₁+x₂+x₃+x₄+x₅+x₆+x₇).                                      (6)

Здесь выражение в скобках — общее количество сотрудников. Задача сводится к определению переменных x_i, минимизирующих целевую функцию Zи удовлетворяющих ограничениям (1)‑(3). Поставленная задача относится к классу линейных оптимизационных задач с ограничениями на переменные и решается с помощью оптимизатора, входящего в состав MSEXCEL. Исходные данные и полученные значения x_iпоказаны на рис. 1.

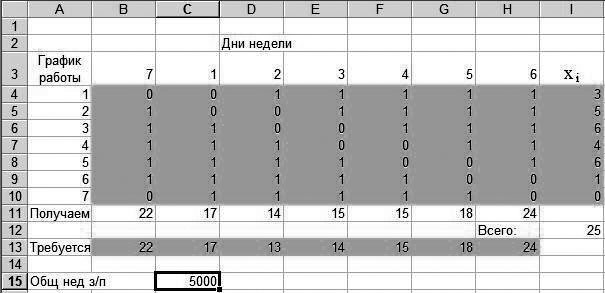
Рисунок 1. Исходные и полученные данные
(фрагмент рабочего листа EXCEL).

Анализ результатов оптимизации, проведенной из различных начальных значений Х, показывает, что решение получается не единственным. Имеется несколько локальных минимумов на поверхности целевой функции. В каждом из них значение целевой функции 5000 и число лишних рабочих выходов равно 2.

Для гарантированного результата поиска глобального минимума рекомендуют применять различные методы поиска и настройки параметров в них, и пробовать поиск из разных точек. Известно, что в ходе решения линейных оптимизационных задач с ограничениями на переменные возможно «заедание» в ходе поиска и траектория поиска не доходит до точки минимума. С целью преодоления этого возможного эффекта были сделаны попытки движения как из разных исходных, так и из найденных точек со сменой способа подсчета разностей. Однако улучшить значение целевой функции не удалось.

Понятно, что лишние рабочие выходы в найденных решениях, а, следовательно, и переплата заработной платы, получились из-за использования пятидневной рабочей недели с двумя днями отдыха подряд. Если ввести графики работы, использующие дни отдыха раздельно и/или неполную рабочую неделю, можно попытаться устранить переплаты. Так, например, в решении, показанном на рис. 1, в графике работы 6 можно во второй и третий дни недели сделать дополнительные выходные. Тогда все ограничения по численности персонала по дням недели будут выполнены с точностью до равенства, численность сотрудников не изменится и будет по-прежнему 25 человек, а общая недельная заработная плата станет равной 4920 у.е. Собственно, мы и ищем варианты организации работ с таким значением заработной платы. Таким образом, возможна ручная доводка графиков работы. Но более интересен формальный математический метод поиска.

Просчитаем ряд вариантов.

Вариант 1. Дополнительно к рассмотренным 7 видам графиков введем еще один график для людей, работающих по половине дня со вторника по субботу.

      В результате оптимизации, проведенной из различных  начальных значений Х, получены различные решения со значениями 5000 целевой функции и двумя лишними рабочими выходами.

        Добиться лучшего решения, по сравнению с базовым решением, не удалось.

Вариант 2. Дополнительно к ранее рассмотренным в базовой задаче 7 видам графиков введем еще 7 аналогичных графиков для людей, работающих по половине дня.

Более широкий набор графиков работы не дал лучшего ответа. Работников в некоторых расчетах стало больше, распределилась нагрузка и на людей, работающих по половине дня, заработная плата та же.

Вариант 3. Персонал формируется из сотрудников, работающих по полной пятидневной рабочей неделе с двумя днями отдыха, и сотрудников,  работающих пять или менее пяти дней в неделю с двумя днями отдыха, которые не обязательно идут подряд.

Поставить математически и решить эту задачу можно либо просчетом большого числа вариантов графиков работы на основе базового примера или расчетом с введением дополнительных переменных для составления выбранного числа графиков работы. Пойдем по второму пути, как более экономичному. Включим в число неизвестных дополнительно к 7 переменным из базовой задачи 7 булевых переменных со значениями 0 или 1 в первой строке матрицы графиков работ. То есть мы в 1 графике работ пытаемся составить последовательность дней работы и отдыха, обеспечивающую наряду с другими графиками работ минимум целевой функции. Задача становится нелинейной и ставится следующим образом:

определить переменные x_i, i= 1,2,…,14 , минимизирующие целевую функцию

Z = 40*( 5*(x₉+x₁₀+x₁₁+x₁₂+x₁₃+x₁₄)+x₈*(x₁+x₂+x₃+x₄+x₅+x₆+x₇))          (7)

и удовлетворяющие ограничениям

x_i³0,       i= 1,2,…,14  ,                                                                          (8)

x_i — целые, i = 1,2,…,14  .                                                                    (9)

x_i — булевы, i = 1,2,…,7  .                                                                   (10)

x₁+x₂+x₃+x₄+x₅+x₆+x₇ £5.                                                                  (11)

x^Т₀A^T ³b^T .                                                                                         (12)

x^Т₀ = (x₈   x₉  x₁₀  x₁₁  x₁₂  x₁₃  x₁₄) .                                                  (13)

b^T = ( 22  17  13  14  15  18  24 ) ,                                                       (14)

                                                               (15)

Результаты оптимизации, проведенной из различных  начальных значений Х и с различными параметрами поиска, получаются разными. Наиболее интересен результат со значением 4920 целевой функции и нулевым числом лишних рабочих дней. Он обеспечивает минимум целевой функции со штатом в 25 человек и выходом на работу каждый день недели минимально необходимого количества сотрудников. Два человека работают по графику 1 — 4 дня выход на работу, 3 дня (1, 5 и 7 дни недели) — отдых.

Таким образом, решение найдено. И при такой постановке задачи наблюдается многозначность решения и возможные остановки поиска в локальных минимумах, далеких от глобального значениях минимума.

Руководство парка отдыха должно располагать несколькими вариантами расчета загрузки персонала и применять нужные из них в зависимости от условий соглашения трудового найма сотрудников. В частности, можно просчитать и другие варианты, например 4 и 5:

Вариант 4. Использование людей, работающих по половине дня 5 дней в неделю с двумя днями отдыха, не идущими подряд:

Вариант 5. Использование людей, работающих по трудовому договору на условиях почасовой оплаты.

Таким образом, в общем случае можно рекомендовать менеджерам следующий метод составления оптимального графика работы персонала на предприятиях:

1.выбрать условия соглашения трудового найма сотрудников;

2.сформулировать математически оптимизационную задачу с ог­раничениями на переменные и решить её с помощью оптимизатора, входящего в состав MSEXCEL;

3.если решение удовлетворяет менеджера, то остановиться, в противном случае расширить условия соглашения трудового найма сотрудников и продолжить поиск.

Список литературы:

1.Горшков А. Ф., Евтеев Б. В., Коршунов В. А. и др. Компьютерное моделирование менеджмента: учебник. 2-е изд., перераб. и дополн. — М.: Изд-во «Экзамен», 2007. — 622 с.