УРАВНИТЕЛЬНЫЕ ВЫЧИСЛЕНИЯ В ПОЛИГОНОМЕТРИЧЕСКОМ ХОДЕ

Статья опубликована в рамках: XXXVII Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 24 декабря 2015 г.)

Наука: Технические науки

Секция: Архитектура, Строительство

Скачать книгу(-и): Сборник статей конференции

Библиографическое описание:

Кротенок А.Ю., Дубиков Д.И. УРАВНИТЕЛЬНЫЕ ВЫЧИСЛЕНИЯ В ПОЛИГОНОМЕТРИЧЕСКОМ ХОДЕ // Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ: сб. ст. по мат. XXXVII междунар. студ. науч.-практ. конф. № 10(36). URL: http://sibac.info/archive/technic/10(36).pdf (дата обращения: 20.04.2024)

Условия публикаций
Все статьи конференции

Проголосовать за статью

Конференция завершена

Эта статья набрала 0 голосов

Дипломы участников

У данной статьи нет
дипломов

УРАВНИТЕЛЬНЫЕ ВЫЧИСЛЕНИЯ В ПОЛИГОНОМЕТРИЧЕСКОМ ХОДЕ

Кротенок Андрей Юрьевич

студент 4 курса, кафедра Горное дело,
РФ, г. Новочеркасск

Е-mail:

" target="_blank">

Дубиков Дмитрий Игоревич

студент 4 курса, кафедра Горное дело,
РФ, г. Новочеркасск

Е-mail: dubikov.dima@mail.ru

Притчина Алла Ивановна

научный руководитель, доцент ГД(МД),
РФ, г. Новочеркасск

На основе выполненных исследований даны рекомендации о выборе способа уравновешивания ходов при создании геодезических сетей методом полигонометрии.

Задачей уравнительных вычислений в полигонометрическом ходе является устранение невязок хода, полученных вследствие ошибок угловых и линейных измерений и ошибок исходных данных.

Таким образом, при уравновешивании одиночного полигонометрического хода в первую очередь необходимо удовлетворить те три условия, которым должны отвечать дирекционные углы и приращения абцисс и ординат сторон хода [1].

При уравновешивании полигонометрических ходов может быть использован упрощенный способ распределения невязок в приращения абцисс и ординат пропорционально длинам сторон. Геометрически этот способ сводится к перемещению пунктов хода параллельно невязке в периметре в направлении, обратном направлению этой невязки.

В зависимости от формы хода его углы и линии получат в результате уравновешивания весьма неравномерные поправки. Так, линия хода, которая параллельна невязке, после уравновешивания совсем не изменит своего направления, но длина её изменится на величину

Линия, перпендикулярная невязке, не изменит длины, но изменит свой дирекционный угол на величину

Следовательно, в полигонометрии 4 класса, имеющей предельную относительную ошибку равную , будем иметь предельную

= ρ=8,2”; а в ходах 1 разряда предельная составляет ; в то время как по требованию нормативных документов [2] СКО измерения угла в 4 классе не должна превышать, а в 1 разряде 5”; при принятом коэффициенте надёжности, равном 2,5 предельные ошибки составят 5” и 12,5”. Имеем явное несоответствие.

Полигонометрические хода могут быть уравновешены по способу наименьших квадратов, но возникает вопрос, каким же способом производить обработку результатов измерений: методом условных измерений (коррелатный метод) или методом посредственных измерений (параметрический метод).

Наиболее выгодным будет тот способ, при котором решается меньшее число условных уравнений.

Из теории способа наименьших квадратов [3] известно, что при уравновешивании методом посредственных измерений число нормальных уравнений равно числу неизвестных, т. е. 2(n-1), где n – число пунктов в ходе.

При уравновешивании методом условных уравнений число нормальных уравнений определяют числом условий, которое равно числу избыточных измерений, следовательно, в одиночном полигонометрическом ходе, независимо от числа сторон, от его длины, будет только три нормальных уравнения.

Задачей настоящих исследований явилось выявление возможности использования упрощенного метода уравновешивания полигонометрических ходов в зависимости от требуемой точности положения хода.

На первом этапе исследований полигонометрический ход, имеющий 17 пунктов и протяжённость в 6147 м был проложен в соответствии с требованиями инструкции к полигонометрическому ходу 4 класса [2] иуравновешен упрощённым методом, в результате чего получены координаты точек хода [табл. 1, гр. 2,3], а относительная ошибка хода составила .

Затем этот же ход был уравнёнкоррелатным методом, в результате которого были получены поправки в измеренные и дирекционные углы, длины линий и приращения координат и по исправленным этими поправками соответствующие величины были уравновешены и получены координаты пунктов хода (табл. 2 гр. 10).

Приняв результаты строгого уравнивания за безошибочные и используя формулы теории ошибок [3] была подсчитана СКО определения координат последней точки хода (M), уравненного упрощенным методом. Для определения этой погрешности из абсолютной погрешности в каждой координате были исключены систематические погрешности (σ), а доля влияния случайных погрешностей рассчитана с учетом их весов.

В результате выполненных расчетов (табл. 1) была получена СКО положения последнего пункта хода, которая составила , при этом абсолютная невязка хода, равная 2М, будет равна 252 мм, тогда относительная погрешность хода , уравненного упрощенным методом, вычисленная через влияние только случайных ошибок, составит

Полученные результаты позволяют сделать вывод: полигонометрические хода 1 и 2 разрядов можно с достаточной точностью уравновешивать упрощённым методом, а полигонометрические хода Государственных геодезических сетей необходимо уравновешивать строгим методом.

Таблица 1.

Поправки к исходным данным

N	Координаты из упрощенного		Координаты из строгого		∆	S, км	σ	δ	δδ
	X	Y	X	Y	X, Y
1	2	3	4	5	6	7	8	9	10	11	12
Селижарово
35	4943,33	8031,52	4943,33	8031,52	0	0,359291	4,1 -3,5	10,9 -0,5	118,90 0,29	2,78 2,78	330,93 0,81
					0
36	4791,649	8357,223	4791,664	8357,219	15	0,212278	2,4 -2,0	14,6 -6,0	212,58 35,47	4,71 4,71	1001,41 167,10
					-4
37	4724,653	8558,643	4724,670	8558,635	17	0,281269	3,2 -2,7	18,8 -16,3	353,20 265,41	3,56 3,56	1255,73 943,61
					-8
38	4557,828	8785,093	4557,850	8785,074	22	0,301947	3,4 -2,9	27,6 -33,1	759,43 1095,10	3,31 3,31	2515,12 3626,79
					-19
39	4321,296	8972,782	4321,327	8972,746	31	0,484969	5,5 -4,7	53,5 -61,3	2859,19 3761,34	2,06 2,06	5895,60 7755,83
					-36
40	3865,76	9139,221	3865,819	9139,155	59	0,521213	5,9418282 -5	32 -31	1027,73 959,80	1,92 1,92	1971,80 1841,48
					-66
42	4022,365	9636,303	4022,403	9636,267	38	0,734815	8,376891 -7	21 -57	425,31 3240,31	1,36 1,36	578,80 4409,70
					-36
43	3703,936	10298,514	3703,965	10298,450	29	0,635979	7,2501606 -6	34 -80	1139,05 6380,10	1,57 1,57	1791,02 10031,93
					-64
44	3304,598	10793,481	3304,639	10793,395	41	0,460892	5,2541688 -4	44 -90	1913,70 8021,28	2,17 2,17	4152,16 17403,82
					-86
45	3137,433	11222,97	3137,482	11222,876	49	0,438921	5,0036994 -4	74 -95	5475,45 8981,96	2,28 2,28	12474,80 20463,72
					-94
46	2795,985	11498,776	2796,064	11498,677	79	0,320025	3,648285 -3	104 -92	10889,28 8448,95	3,12 3,12	34026,34 26400,90
					-99
47	2602,72	11753,849	2602,828	11753,754	108	0,21222	2,419308 -2	124 -91	15272,19 8273,05	4,71 4,71	71963,94 38983,38
					-95
48	2619,767	11965,368	2619,893	11965,275	126	0,268754	3,0637956	146	21297,38	3,72		79244,87
					-93		-3	-86	7467,02	3,72	27783,83
49	2761,268	12193,823	2761,417	12193,734	149	0,154133	1,7571162 -1	166 -86	27636,70 7312,93	6,49 6,49	179304,21 47445,61
					-89
50	2768,015	12347,798	2768,183	12347,711	168	0,245957	2,8039098 -2	202 -81	40883,26 6501,43	4,07 4,07	166221,16 26433,19
					-87
51	2749,586	12593,048	2749,791	12592,965	205	0,514065	5,860341 -5	-6 5	34,34 24,51	1,95 1,95	66,81 47,67
					-83
Подсосонье	2502,462	13043,802	2502,462	13043,802	0
					0
Сумма					1136	6,146728	70,1	1065,9	130297,67	49,78	562794,71
					-959		-59,2	-899,8	70768,95	49,78	233739,38

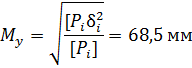
Таблица 2.

Ведомость вычисления координат

Пункты	Измеренные углы	Исправленные углы	Дирекционные углы	Исправленные дир. углы	Длины линий, м	Исправленные длины линий, м	Вычисленные приращения, м		Исправленные приращения, м		Координаты, м
1	2	3	4	5	6	7	8		9		10
							Δх	Δу	Δх	Δу	Х	Y
Селижарово
	6,9		216°22’17”
35	78°35’40”	78°35’46,9”			-0,011		-0,006	-0,015			4943,33	8031,52
	6,3		114°58'3,9"		359,302	359,291	-151,66	325,714	-151,666	325,699
36	173°25’36”	173°25’42,3”			-0,006		-0,004	-0,008			4791,664	8357,219
	6,1		108°23'46,2"		212,278	212,272	-66,99	201,424	-66,994	201,416
37	197°58’48”	197°58’54,1”			-0,008		-0,002	-0,011			4724,670	8558,635
	5,1		126°22'40,3"		281,269	281,261	-166,818	226,45	-166,820	226,439
38	195°11’19”	195°11’24,1”			-0,007		0,000	-0,010			4557,850	8785,074
	3,4		141°34'4,4"		301,947	301,94	-236,523	187,682	-236,523	187,672
39	198°21’42”	198°21’45,4”			-0,008		0,005	-0,010			4321,327	8972,746
	-0,3		159°55'49,8"		484,969	484,961	-455,513	166,419	-455,508	166,409
40	92°35’09”	92°35’8,7”			-0,013		-0,003	-0,010			3865,819	9139,155
	2,3		72°30'58,5"		521,213	521,2	156,587	497,122	156,584	497,112
42	223°09’54”	223°09’56,3”			-0,022		0,002	-0,023			4022,403	9636,267
	0,9		115°40'54,8"		734,815	734,793	-318,44	662,206	-318,438	662,183
43	193°12’53”	193°12’53,9”			-0,017		0,008	-0,010			3703,965	10298,450
	-1,5		128°53'48,7"		635,979	635,962	-399,334	494,955	-399,326	494,945
44	162°22’13”	162°22’11,5”			-0,014		0,008	-0,012			3304,639	10793,395
	-2,1		111°16'0,2"		460,892	460,878	-167,165	429,493	-167,157	429,481
45	209°48’10”	209°48’7,9”			-0,011		0,011	-0,003			3137,482	11222,876
	-4,5		141°4'8,1"		438,921	438,91	-341,429	275,804	-341,418	275,801
46	166°04’47”	166°04’42,5”			-0,009		0,011	-0,003			2796,064	11498,677
	-5,7		127°08'50,6"		320,025	320,016	-193,247	255,08	-193,236	255,077
47	138°14’36”	138°14’30,3”			-0,006		0,005	-0,006			2602,828	11753,754
	-5		85°23'20,9"		212,22	212,214	17,06	211,527	17,065	211,521
48	152°50’11”	152°50’06”			-0,006		0,002	-0,008			2619,893	11965,275
	-3,2		58°13'26,9"		268,754	268,748	141,522	228,467	141,524	228,459
49	209°15’42”	209°15’38,3”			-0,004		0,002	-0,004			2761,417	12193,734
	-2,8		87°29'5,2"		154,133	154,129	6,764	153,981	6,766	153,977
50	186°48’20”	186°48’17,2”			-0,007		0,004	-0,007			2768,183	12347,711
	-2,4		94°17'22,4"		245,957	245,95	-18,396	245,261	-18,392	245,254
51	204°26’05”	204°26’2,6”			-0,015		0,010	-0,010			2749,791	12592,965
	-3,6		118°43'25"		514,065	514,05	-247,045	450,795	-247,035	450,785
Подсосонье	328°24’50”	328°24’46,4”									2502,462	13043,802
			267°08'11,4"
						6146,575	-2440,627	5012,38

							fx=0,053	fy=-0,15
							0,16	1/38600

Список литературы:

Антонюженко В.Б. Уравновешивание полигонометрических сетей. – М.: Издательство геодезической литературы, 1962.
Инструкция по топографической съемке в масштабах 1:5000, 1:2000, 1:1000 и 1:500 (Главное уравнивание геодезии и картографии при Совете Министров СССР. – М., Недра, 2007.
Кемниц Ю.В. Теория ошибок измерений. – М.: издательство «Недра», 1967.

Проголосовать за статью

Конференция завершена

Эта статья набрала 0 голосов

Дипломы участников

У данной статьи нет
дипломов

Оставить комментарий