Статья опубликована в рамках: XXII Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 15 июля 2014 г.)
Наука: Технические науки
Секция: Электротехника
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
РЯДЫ ФУРЬЕ И ИХ ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ В ЭЛЕКТРОТЕХНИКЕ
Гевелюк Игорь Витальевич
студент 1 курса, кафедра электротехники и электроэнергетики ДВФУ, РФ, г. Владивосток
E -mail:
Дмух Галина Юрьевна
научный руководитель, канд. пед. наук, доцент кафедры алгебры, геометрии и анализа ШЕН ДВФУ, РФ, г. Владивосток
В данной статье поднимается тема прикладного применения ряда Фурье в электротехнике. Рассматриваются основные аспекты, касающиеся теории. Для большей наглядности приведены примеры, которые демонстрируют использование ряда Фурье в инженерной практике электроэнергетика.
Основные понятия: ряд Фурье, функция, ортогональная система, тригонометрический ряд, функциональный ряд, период.
Математика является одной из немногих наук, которые широко используются на практике. Любой производственно-технологический процесс не обходится без фундаментальных математических закономерностей. Эффективное применение различных инструментов математического аппарата позволяет конструировать устройства и автоматизированные агрегаты, способные выполнять операции с высоким уровнем точности, выполнять сложные расчеты и вычисления при проектировании зданий и сооружений, производить необходимые вычисления при геодезических исследованиях. Подобная тесная связь, приводит к взаимному обогащению, как самой математики, так и прикладных дисциплин. Зачастую, идеи и методы, созданные для решения частных задач, принимают общий характер и требуют строгого обоснования. Те методы, которые выдержали всесторонние проверки и весьма длительные испытания, в последствие становятся математическими теориями. В дальнейшем эти теории используются при решении более широкого круга задач, нежели те, на основе которых они были созданы. Инженерная практика в значительной мере ориентирует и стимулирует развитие математического аппарата.
Именно от того, что элементы математики встречаются на производстве практически на каждом шагу, специалистам важно знать и блестяще ориентироваться в области применения тех или иных инструментов анализа и расчета. Например, инженеру-электротехнику для расчетов периодических несинусоидальных процессов следует иметь четкое представление о таком важном понятии, как ряд Фурье.
Теперь обратимся к теории. Рассмотрим два наиболее встречающихся типа рядов Фурье.
Ряд Фурье по ортогональной системе функций . Пусть функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() или имеет на этом отрезке конечное число точек разрыва первого рода. Рядом Фурье такой функции
или имеет на этом отрезке конечное число точек разрыва первого рода. Рядом Фурье такой функции ![]() на отрезке
на отрезке ![]() по ортогональной системе
по ортогональной системе ![]() называется ряд
называется ряд
 ,
,
коэффициенты которого определяются равенствами
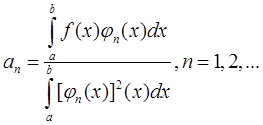
Если ряд Фурье функции ![]() по системе
по системе ![]() сходится к
сходится к ![]() в каждой ее точке непрерывности, то говорится, что функция
в каждой ее точке непрерывности, то говорится, что функция ![]() разлагается в ряд по ортогональной системе
разлагается в ряд по ортогональной системе ![]() . Очевидно, что если функция
. Очевидно, что если функция ![]() разлагается в ряд по некоторой ортогональной системе функций, то это разложение единственно.
разлагается в ряд по некоторой ортогональной системе функций, то это разложение единственно.
Тригонометрические ряды Фурье. Наиболее широко в электротехнике применяются ряды Фурье по основной тригонометрической системе функций, т. е. по системе функций
 (1.0)
(1.0)
Ряд Фурье по основной тригонометрической системе функций (1.0) называется тригонометрическим рядом Фурье. Он записывается в виде

Коэффициенты ![]() и
и ![]() рассчитываются по формулам
рассчитываются по формулам
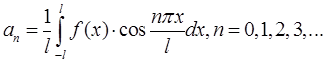 ,
,
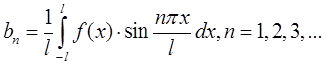
Кроме всего этого, стоит сказать о сумме тригонометрического ряда Фурье. Все функции системы (1.0) являются периодическими с общим периодом ![]() . Поэтому если ряд сходится на отрезке
. Поэтому если ряд сходится на отрезке ![]() , то он сходится и на всей числовой оси, а его сумма периодически повторяет те значения, которые она принимала на отрезке
, то он сходится и на всей числовой оси, а его сумма периодически повторяет те значения, которые она принимала на отрезке ![]() . Таким образом, можно говорить не только о разложении в тригонометрический ряд Фурье функции
. Таким образом, можно говорить не только о разложении в тригонометрический ряд Фурье функции ![]() на отрезке
на отрезке ![]() , но и о разложении в ряд периодической функции, которая будет являться периодическим продолжением ( имея период
, но и о разложении в ряд периодической функции, которая будет являться периодическим продолжением ( имея период ![]() ) на всю числовую ось.
) на всю числовую ось.
Пример 1:
Формулировка задачи: Вычислить суммарный ток в схеме на рис. 1.
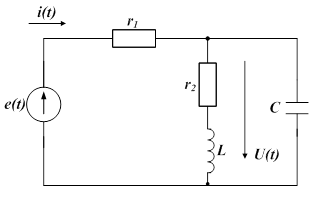
Рисунок 1. Электрическая цепь
Задано:
![]() В;
В;
![]() ;
; ![]() ;
; ![]() ;
; ![]()
Решение:
Сопротивление постоянному току ![]() Постоянная слагающая тока:
Постоянная слагающая тока:

Комплексное сопротивление цепи для основной частоты:
![]()
Комплексная амплитуда тока основной частоты:

Комплексное сопротивление цепи для утроенной частоты:
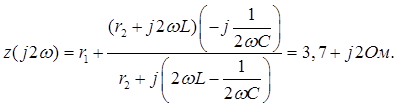
Комплексная амплитуда тока третьей гармоники:
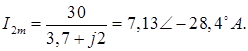
Таким образом, искомое значение суммарного тока будет иметь вид:
![]()
Пример 2:
Формулировка задачи: Вычислить активную мощность, поступающую в цепь при
![]() В;
В; ![]()
Решение:
По формуле  рассчитаем искомую величину мощности:
рассчитаем искомую величину мощности:

![]() Вт.
Вт.
Список литературы:
1.Атабеков Г.И. А92 Теоретические основы электротехники. Линейные электрические цепи: Учебное пособие. 7-е изд., стер. СПб.: Издательство «Лань», 2009. — 592 с.: ил. — (Учебники для вузов. Специальная литература).
2.Жежеленко И.В. Высшие гармоники в системах электроснабжения промпредприятий 2-е изд., перераб. и доп. М.: Энергоатомиздат, 1984. — 160 с.
3.Сигорский В.П. Математический аппарат инженера. Изд. 2-е стереотипное. “Технiка”, 1997. — 768 с.
дипломов


Оставить комментарий