Статья опубликована в рамках: XXII Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 15 июля 2014 г.)
Наука: Технические науки
Секция: Телекоммуникации
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
АСИМПТОТИЧЕСКОЕ ПОВЕДЕНИЕ СТАЦИОНАРНОГО РАСПРЕДЕЛЕНИЯ СМО С БОЛЬШИМ ОБЪЕМОМ БУФЕРА
Бойченко Станислав Борисович
студент 4 курса, институт телекоммуникационных систем НТУУ «КПИ», Украина, г. Киев
E-mail: stas 123123@gmail.com
Пилипенко Андрей Юрьевич
научный руководитель, д-р физ.-мат. наук, проф. ИТС НТУУ «КПИ», Украина, г. Киев
Все процессы в реальном мире можно так или иначе представить в виде математических моделей. Особняком стоят модели систем массового обслуживания. Почти всё ТК оборудование является СМО (сервера, коммутаторы, маршрутизаторы), на чей вход подаётся заявка/пакет/набор данных, которые обрабатываются и идут на выход. Одним из важнейших вопросов: при каких условиях произойдёт отказ оборудования? Когда нужно включить дублирующий сервер? Или когда мощностей оборудования слишком много?
Далее будем рассматривать систему ![]() , как одну из самых интересных с точки зрения практики. То есть, количество заявок в системе в один момент может либо увеличиться на величину от 1 до Х, либо уменьшиться на величину от 1 до Y, либо не измениться. Теперь ограничим буфер, т. е. максимальное количество заявок, неким числом N, которое будет гораздо больше X или Y. Теперь интересно, как же всё-таки зависит вероятность отказа системы от X,Y,N.
, как одну из самых интересных с точки зрения практики. То есть, количество заявок в системе в один момент может либо увеличиться на величину от 1 до Х, либо уменьшиться на величину от 1 до Y, либо не измениться. Теперь ограничим буфер, т. е. максимальное количество заявок, неким числом N, которое будет гораздо больше X или Y. Теперь интересно, как же всё-таки зависит вероятность отказа системы от X,Y,N.
Данную систему можно представить в виде цепи Маркова, где каждому состоянию будет соответствовать количество заявок в системе (от 1 до N), а ![]() — вероятности перехода, соответствующие определённому количеству (в индексе) обработанных (отрицательные индексы) или полученных заявок (положительные индексы) [3].
— вероятности перехода, соответствующие определённому количеству (в индексе) обработанных (отрицательные индексы) или полученных заявок (положительные индексы) [3].
Если система имеет стационарное распределение, то имеем рекуррентное уравнение
|
|
(1) |
Далее, записав для него характеристическое, найдём параметры λ. Известно, что их количество меньше количества вероятностей перехода на 1, и один из этих параметров равен единице. Получим
|
|
(2) |
где A — неизвестные константы [1] Для их нахождения можно составить систему уравнений. Для этого в соотношение (1) подставим (2) и запишем уравнения для первых X и последних Y вероятностей, т. е. для таких, которые не вписываются в общую «схему» рекуррентных уравнений для данной системы в том смысле, что в них будут отсутствовать часть слагаемых:
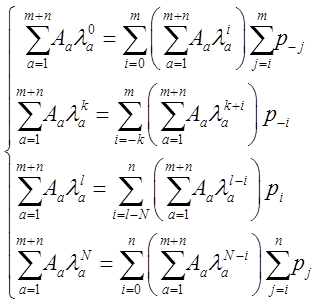 (3)
(3)
Эти уравнения будут линейно зависимые, поэтому воспользуемся известным тождеством [2]
|
|
(4) |
И заменим на него последнее уравнение в системе:
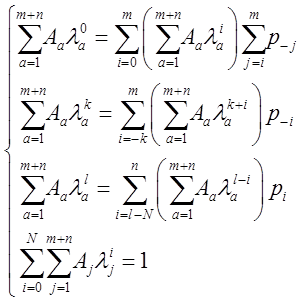 (5)
(5)
Далее, путем математических преобразований, данную систему можно записать в матричном виде так:
 (6)
(6)
Видно, что решение зависит от N, соответственно и распределение будет зависеть от него. Для того, чтобы проверить как именно, исследуем данную зависимость с помощью пакета MathCad. Просто записываем данные формулы, как функции от N и выводим графики зависимости коэффициентов от N.
Например, при 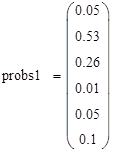 , где 0,16 соответствует
, где 0,16 соответствует ![]() , а 0,05 и 0,1 -
, а 0,05 и 0,1 - ![]() и
и ![]() соответственно, получим (рис. 1).
соответственно, получим (рис. 1).
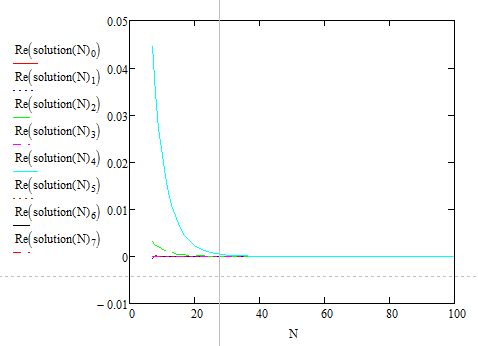
Рисунок 1. Коэффициенты А
Замечание: при решении характеристического уравнения могут получиться комплексные комплексно сопряженные корни. Соответствующие им коэффициенты также будут комплексно сопряженными. Но вероятности не будут комплексными, т. к. мнимые части сократятся; и как видно из графиков, больший «вес» имеет коэффициент чисто действительный.
На «концах цепи» получим (рис. 2)

Рисунок 2. ![]() и
и ![]() , а также их логарифмы, в зависимости от объема буфера
, а также их логарифмы, в зависимости от объема буфера
Где head и tail — ![]() и
и ![]() соответственно. Что интересно, если «отбросить» из формулы (2) все слагаемые, кроме того, что соответствует |λ|>1 (рис. 3):
соответственно. Что интересно, если «отбросить» из формулы (2) все слагаемые, кроме того, что соответствует |λ|>1 (рис. 3):
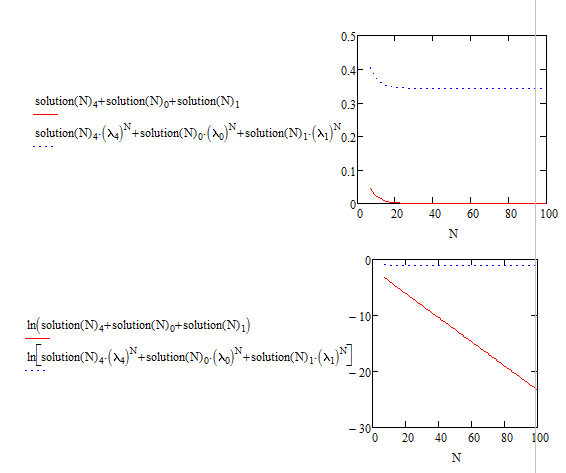
Рисунок 3. Упрощённое представление π 0 и πN![]()
Видно, что скорость изменения обоих параметров соответствует приведенным суммам.
Далее, путем вариации входных значений, можно получить такие выводы:
1. Стационарное распределение количества заявок в системе практически не зависит от объема буфера: на одном конце оно постоянное, на другом — стремится к нулю как константа в степени объема буфера.
2. Распределение симметрично для различных мат. ожиданий приходящих заявок, т. е. при отрицательном (обрабатывается больше, чем приходит) — то буфер простаивает, и наоборот — при положительном — заполнен с большей вероятностью
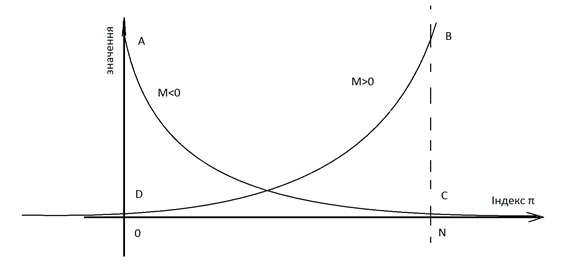
Рисунок 4. Распределение значений πі для случаев з положительным и отрицательным математическим ожиданием
3. Из предыдущего пункта, можно сказать, что для реальных систем, где нагрузка варьируется, можно подобрать интенсивность обработки и объем буфера (можно даже динамически) таким образом, чтоб обеспечить требуемый уровень отказоустойчивости системы.
Список литературы:
1.Бочарова И.Е. Решение рекуррентных уравнений// Конспект лекций по курсу “Базовые алгоритмы обработки информации”. — 2009. — [Электронный ресурс] — Режим доступа. — URL: http://k14.spb.ru/cm/uploads/105/014 (дата обращения 12.06.14).
2.Тихонов В., Бакаев Ю. Статистическая теория радиотехнических устройств. М.: ВВИО, 1978.
3.Adan I., Resing J. Queueing Theory: Ivo Adan and Jacques Resing. Eindhoven University of Technology. Department of Mathematics and Computing Science, 2001.
дипломов


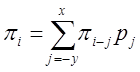
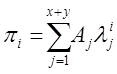
Оставить комментарий