МОДЕЛИРОВАНИЕ  ПРОЦЕССА  ГОРЯЧЕЙ  ПРОКАТКИ  В  ПРОГРАММНОМ  КОМПЛЕКСЕ  DEFORM   3D  КАК  МЕТОД  ОЦЕНКИ  ПРИГОДНОСТИ  ФОРМУЛ  ДЛЯ  РАСЧЕТА  ИЗМЕНЕНИЙ  ТЕМПЕРАТУРЫ  МЕТАЛЛА  В  ОЧАГЕ  ДЕФОРМАЦИИ

Разгулин  Игорь  Андреевич

студент  4  курса,  кафедра  обработки  металлов  давлением  МГТУ,  РФ,  г.  Магнитогорск

E -mail:  igor.darsy@mail.ru

Белов  Владимир  Игоревич

студент  4  курса,  кафедра  обработки  металлов  давлением  МГТУ,  РФ,  г.  Магнитогорск

E -mail:  beliyvovan@yandex.ru

Румянцев  Михаил  Игоревич

научный  руководитель,  канд.  техн.  наук,  профессор  МГТУ,  РФ,  г.  Магнитогорск

«DEFORM  —  система  конечно-элементного  моделирования,  которая  предназначена  для  анализа  трехмерного  течения  металла  при  различных  процессах  обработки  металлов  давлением.  DEFORM  —  практичный  и  эффективный  инструмент,  позволяющий  прогнозировать  характер  формообразования  при  операциях  обработки  металлов  давлением  без  существенных  затрат  на  экспериментальное  исследование»  [2,  с.  6].

При  разработке  и  анализе  процесса  горячей  прокатки  большое  значение  имеет  задача  оценки  изменения  температуры  металла  в  очаге  деформации,  которое  является  следствием  охлаждения  в  результате  теплоотдачи  рабочим  валкам  ()  и  разогрева()  за  счет  энергии  пластической  деформации  [3]. 

Известно  много  формул  для  расчета  величин    и  ,  но  каждая  из  них  выведена  с  определенными  допущениями.  Чтобы  оценить  применимость  той  или  другой  формулы  в  конкретных  условиях  прокатки  необходимо  сравнить  результаты  расчета  по  данной  формуле  с  результатами  эксперимента.  Однако  при  физическом  эксперименте  выделить  доли    и    в  итоговом  изменении  температуры  затруднительно.  Поэтому  в  данном  исследовании  расчеты  по  различным  формулам  сравнивали  с  результатами  моделирования  в  программном  комплексе  DEFORM  3D,  который  позволяет  проводить  анализ  процесса  прокатки  при  минимальном  количестве  допущений  [4]. 

Для  исследования  были  поставлены  две  задачи  и,  соответственно,  созданы  две  конечно-элементные  модели,  а  в  качестве  тестовых  выбрали  примеры  из  книги  [1].  В  одном  из  них  (стр.  149)  рассматривается  расчет  охлаждения  при  взаимодействии  с  рабочими  валками,  а  в  другом  (стр.  160)  —  расчет  разогрева  в  результате  пластической  деформации.

Охлаждение  металла  за  счет  передачи  тепла  валкам  исследовали  для  следующего  случая  прокатки:  полоса  из  стали  08  кп;  толщина  перед  деформацией  =20,  а  после  деформации  =10  мм;  исходная  температура  металла  =900  °С;  температура  валков  =85  °С;  радиус  валков  400  мм,  а  скорость  их  вращения  18,785  с^-1.  При  моделировании  были  приняты  следующие  допущения:  материал  —  сталь  AISI  1045  из  базы  данных  программного  комплекса;  деформируемая  среда  жестко-пластичная;  валки  жесткие;  число  шагов  —  25,  каждый  длительностью  по  0,05  с;  контактное  трение  отображается  законом  Зибеля  при  =  0,3;  коэффициент  теплопередачи  между  валками  и  заготовкой  —  11  Н/с/мм/°С,  коэффициент  перехода  механической  энергии  в  тепловую  равен  0.  На  рис.  1  представлены  распределения  температуры  по  толщине  полосы  в  сечениях  входа  и  выхода  очага  деформации.

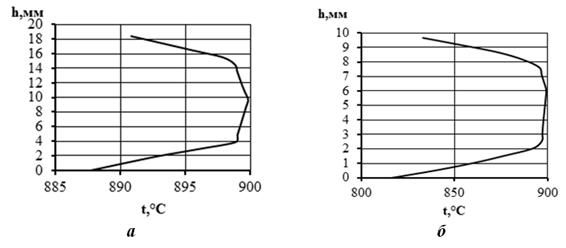
Рисунок  1.  Распределение  температуры  металла  по  толщине  полосы  в  сечениях  входа  (а)  и  выхода  (б)

На  входе  в  очаг,  вследствие  предварительного  охлаждения,  температура  поверхности  полосы  стала  примерно  на  10  С  меньше,  чем  в  середине,  а  среднее  по  толщине  значение  равно  896  С  (определено  численным  интегрированием  по  методу  трапеций).  На  выходе  из  очага  градиент  температуры  увеличился  до  20  С,  причем  температура  в  середине  полосы  за  время  перемещения  металла  через  очаг  деформации  не  изменилась.  Средняя  по  толщине  сечения  выхода  температура  равна  880  С.  Таким  образом,  при  граничных  условиях  тестового  примера  охлаждение  полосы  в  результате  теплопередачи  валкам  =16  С.  На  рис.  2  приведен  график,  иллюстрирующий  различия  между  полученным  значением  и  значениями  ,  рассчитанным  по  различным  формулам.

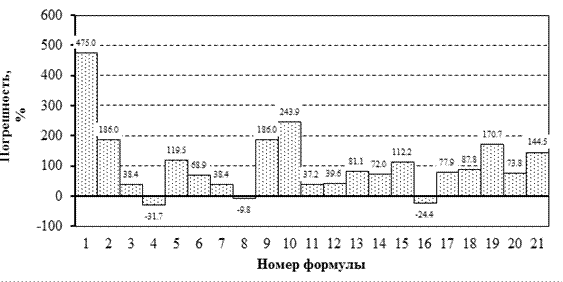
Рисунок  2.  Погрешности  расчета  по  различным  формулам:

1  —  В.  Тринкс;  2  —  В.А.  Тягунов;  3  —  Г.П.  Иванцов;  4  —  Ш.  Гелеи;  5  —  Н.Н.  Крейндлин;  6  —  Х.  Венцель;  7  —  Ю.Д.  Железнов,  Б.А.  Цифринович;  8  —  О.  Повельски;  9  —  Ф.  Серединский;  10  —  В.М.  Луговской;  11  —  Ю.В.  Коновалов,  А.Л.  Остапенко;  12  —  Ю.В.  Коновалов,  А.Л.  Остапенко;  13  —  С.Л.  Коцарь,  Б.А.  Поляков,  М.И.  Псел;  14  —  И.М.  Меерович,  И.Ф.  Франценюк,  Ю.Д.  Железнови  др.;  15  —  И.  Шварцер;  16  —  У.  Лангер;  17  —  В.И.  Зюзин,  М.Д.  Залесов,  Л.Д.  Ломтев;  18  —  Х.  Какадо,  Х.  Нишимура,  К.  Нишимура;  19  —  Ю.В.  Коновалов,  А.Л.  Остапенко,  В.И.  Пономарев;  20  —  И.  Шварцер;  21  —  Ю.В.  Коновалов,  А.Л.  Остапенко,  В.И.  Пономарев

Наименьшая  по  модулю  погрешность  (9,76%)  получается  при  расчете  по  формуле  О.  Повельски:

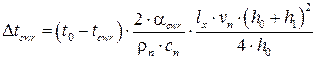                       (1)

где:  —  коэффициент  теплопередачи  на  контакте  валка  и  полосы; 

—  плотность  полосы,  кг/м³; 

—  теплоемкость  полосы,  Дж/кг·К; 

—  скорость  выхода  полосы  из  валков,  м/с; 

—  длина  очага  деформации,  м.

Разогрев  металла  за  счет  деформации  исследовали  для  следующего  случая  прокатки:  полоса  из  низкоуглеродистой  стали;  =33,5  и  =17,2  мм;  =975  °С;  =79,5  мм;  =0,97  м/с.  При  моделировании  были  приняты  следующие  допущения:  материал  —  сталь  AISI  1045  из  базы  данных  программного  комплекса;  деформируемая  среда  жестко-пластичная;  валки  жесткие;  число  шагов  —  27,  каждый  длительностью  по  0,25  с;  контактное  трение  отображается  законом  Зибеля  при  =  0,3;  коэффициент  перехода  механической  энергии  в  тепловую  равен  0,75.  На  рис.  3  представлены  распределения  температуры  по  толщине  полосы  в  сечениях  входа  и  выхода  очага  деформации. 

Рисунок  3.  Распределение  температуры  металла  по  толщине  полосы  в  сечениях  входа  (а)  и  перед  сечением  выхода  (б)

После  входа  в  очаг  деформации  происходит  разогрев  полосы  примерно  на  2  С,  температура  поверхности  полосы  примерно  на  0,5  С  меньше,  чем  в  середине.  Среднее  по  толщине  значение  равно  976,5  С.На  выходе  из  очага  температура  в  середине  полосы  возросла  примерно  на  10—15  С,  а  в  приконтактных  слоях  разогрев  достигает  50—60  С.  Градиент  температуры  увеличился  до  40  С,  а  средняя  по  толщине  температура  равна  1010°С.  Таким  образом,  при  граничных  условиях  тестового  примера  разогрев  полосы  в  результате  пластической  деформации=33,5  С.  На  рис.  4  приведен  график,  иллюстрирующий  различия  между  полученным  значением  и  значениями  ,  рассчитанными  по  различным  формулам. 

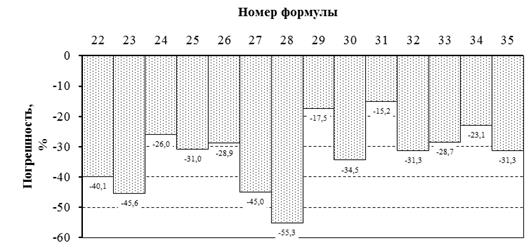
Рисунок  4.  Погрешности  расчета  по  различным  формулам:

22  —  А.И.  Целиков;  23  —  Л.Г.  Стукач;  24  —  В.А.  Тягунов;  25  —  Н.И.  Крендлин;  26  —  Ю.Д.  Железнов  Б.А.  Шифринович;  27  —  М.А.  Зайков;  28  —  Х.  Венцель;  29  —  С.Л.  Коцарь,  Б.А.  Поляков,  М.И.  Псел;  30  —  О.  Павельски;  31  —  В.И.  Зюзин,  М.Я.  Бровман,  А.Ф.  Мельников;  32  —  И.  Шварцер;  33  —  В.М.  Логовской;  34  —  Ю.В.  Коновалов,  А.Л.  Остапенко,  В.И.  Пономарев;  35  —  И.  Шварцер

Во  всех  случаях  значения,  рассчитанные  по  анализируемым  формулам,  меньше  найденного  компьютерным  моделированием.  Наименьшая  по  модулю  погрешность  (15,2  %)  получается  при  расчете  по  формуле,  авторами  которой  являются  В.И.  Зюзин,  М.Я.  Бровман,  А.Ф.  Мельников:

,                                   (2)

где:—  среднее  контактное  давление.

Несколько  большая  величина  погрешности  (17,5  %  по  модулю)  наблюдается  при  использовании  формулы  С.Л.  Коцаря,  Б.А.  Полякова  и  М.И.  Псела:

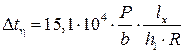,                                       (3)

где:  —  усилие  прокатки,  МН;

—  ширина  полосы,  м; 

—  радиус  валка,  мм.

Формулы  (1—3)  дают  наименьшие  погрешности  для  условий  тестовых  примеров.  Дальнейшее  исследование  будет  состоять  в  моделировании  прокатки  и  оценке  погрешностей  расчетных  формул  при  других  граничных  условиях  из  всего  диапазона  возможных  значений  для  горячей  листовой  прокатки.  Таким  образом  будут  определены  рекомендации  по  выбору  формул,  которые  позволят  наиболее  точно  прогнозировать  температуру  металла  во  время  прокатки  толстых  листов  на  стане  5000  ОАО  «ММК»  для  конкретной  совокупности  граничных  условий.  Тем  самым  повысится  точность  соблюдения  режимов  термомеханической  прокатки  и  снизится  выход  продукции  с  неудовлетворительными  свойствами. 

Список  литературы:

1.Коновалов  Ю.В.,  Остапенко  А.Л.,  Пономарев  В.И.  Расчет  параметров  листовой  прокатки.  Справочник.  М.:  «Металлургия»,  1986.  —  429  с.

2.Паршин  B.C.,  Карамышев  А.П.,  Некрасов  И.И.,  Пугин  А.И.,  Федулов  А.А.  Практическое  руководство  к  программному  комплексу  DEFORM-3D:учеб.  пособие.  Екатеринбург:  УрФУ,  2010.  —  266  с.

3.Целиков  А.И.,  Никитин  Г.С.,  Рокотян  С.Е.  Теория  продольной  прокатки.  М.:  «Металлургия»,  1980.  —  319  с.

4.Shiro  Kobayashi,  Soo-Ik  Oh,  Taylan  Altan.  Metal  Forming  and  the  Finite-  Element  Method.  New  York,  Oxford  «Oxford  University  Press»,  1989.  —  198  p.