Статья опубликована в рамках: XXII Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 15 июля 2014 г.)
Наука: Технические науки
Секция: Металлургия
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ОЦЕНКА С ПРИМЕНЕНИЕМ ПРОГРАММНОГО КОМПЛЕКСА DEFORM 3D СРЕДНИХ ЗНАЧЕНИЙ ТЕМПЕРАТУРЫ, СТЕПЕНИ И СКОРОСТИ ДЕФОРМАЦИИ ПРИ ГОРЯЧЕЙ ПРОКАТКЕ
Белов Владимир Игоревич
студент 4 курса, кафедра обработки металлов давлением ФГБОУ ВПО МГТУ «им. Г.И. Носова», РФ, г. Магнитогорск
E-mail : beliyvovan@yandex.ru
Разгулин Игорь Андреевич
студент 4 курса, кафедра обработки металлов давлением ФГБОУ ВПО МГТУ «им. Г.И. Носова», РФ, г. Магнитогорск
E-mail:
Румянцев Михаил Игоревич
научный руководитель, канд. тех. наук, профессор ФГБОУ ВПО МГТУ «им. Г.И. Носова», РФ, г. Магнитогорск
При разработке и анализе процесса горячей прокатки в режиме реального времени, например при автоматическом управлении процессом прокатки, важное значение имеет задача определения усредненных значений термомеханических параметров (степени ![]() , скорости
, скорости ![]() и температуры
и температуры ![]() деформирования) в очаге деформации. В дальнейшем эти усредненные значения применяются в расчете сопротивления металла деформации на основании которого оцениваются усилие, момент и мощность прокатки. Чтобы повысить точность прогноза указанных параметров, а значит и повысить точность выводов относительно возможности осуществления процесса, необходимо выбрать среди известных формул [2, с. 230] наиболее точные зависимости для расчета
деформирования) в очаге деформации. В дальнейшем эти усредненные значения применяются в расчете сопротивления металла деформации на основании которого оцениваются усилие, момент и мощность прокатки. Чтобы повысить точность прогноза указанных параметров, а значит и повысить точность выводов относительно возможности осуществления процесса, необходимо выбрать среди известных формул [2, с. 230] наиболее точные зависимости для расчета ![]() ,
, ![]() и
и ![]() . В данном исследовании значения параметров, полученные с помощью программы DEFORM 3D, которая позволяет моделировать процессы обработки металлов давлением при минимуме упрощающих допущений [3, с. 154], рассматриваются как действительные.
. В данном исследовании значения параметров, полученные с помощью программы DEFORM 3D, которая позволяет моделировать процессы обработки металлов давлением при минимуме упрощающих допущений [3, с. 154], рассматриваются как действительные.
В качестве примера рассматривается деформация раската размерами 186´1950´5150 мм с обжатием 20 мм. Диаметр валков 1000 мм, скорость их вращения 2,73 рад/с. Таким условиям соответствует высота очага деформации ![]() =1,07. Температура раската 1210 °С, окружающего воздуха 20 °С. При постановке задачи принято: среда жестко-пластическая; марка прокатываемой стали AISI-1045; контактное трение по Зибелю при
=1,07. Температура раската 1210 °С, окружающего воздуха 20 °С. При постановке задачи принято: среда жестко-пластическая; марка прокатываемой стали AISI-1045; контактное трение по Зибелю при ![]() = 0,25. Для сляба и обоих валков сгенерировали сетку, состоящую из 8000 элементов.
= 0,25. Для сляба и обоих валков сгенерировали сетку, состоящую из 8000 элементов.
Усредненные значения каждого параметра определяли интегрированием по методу трапеций массива значений, которые соответствуют 10 сечениям, расположенным по длине ![]() очага деформации с шагом
очага деформации с шагом ![]() и в точках, распределенных по высоте
и в точках, распределенных по высоте ![]() каждого сечения с шагом
каждого сечения с шагом ![]() .
.
Для оценки средней степени деформации ![]() исследовали распределение интенсивности деформации
исследовали распределение интенсивности деформации ![]() . На рис. 1 в качестве примера показаны распределения
. На рис. 1 в качестве примера показаны распределения ![]() по высоте очага деформации вблизи сечений входа и выхода.
по высоте очага деформации вблизи сечений входа и выхода.
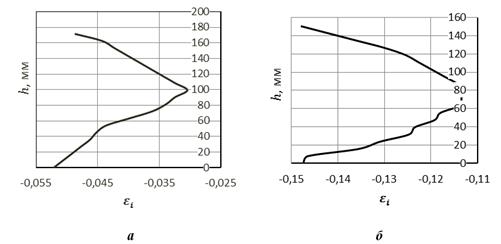
Рисунок 1. Распределение интенсивности деформации по высоте очага вблизи сечения входа (а) и выхода (б)
Применительно к анализируемому случаю в начале очага деформации ![]() находится в пределах от –0,03 до –0,055. К сечению выхода из очага деформации
находится в пределах от –0,03 до –0,055. К сечению выхода из очага деформации ![]() возрастает в три раза и находится в пределах от –0,13 до –0,15. Наибольшая интенсивность деформации наблюдается у контактной поверхности. Среднее в пределах очага значение интенсивности деформации, т. е. величина степени деформации
возрастает в три раза и находится в пределах от –0,13 до –0,15. Наибольшая интенсивность деформации наблюдается у контактной поверхности. Среднее в пределах очага значение интенсивности деформации, т. е. величина степени деформации ![]() , равна 0,192. Сравнение полученного значения с результатами расчетов степени деформации по различным формулам (табл. 1) показывает, что наименьшую погрешность дает вычисление степени деформации по формуле (1), т. е. как относительного обжатия первого вида.
, равна 0,192. Сравнение полученного значения с результатами расчетов степени деформации по различным формулам (табл. 1) показывает, что наименьшую погрешность дает вычисление степени деформации по формуле (1), т. е. как относительного обжатия первого вида.
Таблица 1.
Погрешность расчета степени деформации по различным формулам
|
Формула |
Значение |
Погреш- ность,% |
|
|
|
(1) |
0,22 |
17,60 |
|
|
(2) |
0,25 |
32,29 |
|
|
(3) |
0,15 |
-21,59 |

Рисунок 2. Распределение скорости деформации по высоте очага вблизи сечения входа (а) и выхода (б)
Для оценки средней скорости деформации ![]() исследовали распределение по длине и высоте очага скорости деформации сжатия
исследовали распределение по длине и высоте очага скорости деформации сжатия ![]() . На рис. 2 в качестве примера показаны распределения
. На рис. 2 в качестве примера показаны распределения ![]() по высоте очага деформации вблизи сечений входа и выхода.
по высоте очага деформации вблизи сечений входа и выхода.

Рисунок 3. Погрешность оценивания средней скорости деформации по различным формулам: С. Экелунд (1), Л. Вайс (2), В. Тринкс (3), Х. Гофф и Т. Даль (4), А.А. Королев (5), Д.И. Старченко (6), Р. Симс (7), А.И. Целиков (8), В.Н. Выдрин (9)
Закономерности распределения ![]() по длине и высоте очага такие же, как у распределения интенсивности деформации — от сечения входа к сечению выхода скорость деформации возрастает (от –0,07…–0,085 до –0,09…–0,115), а наибольшие значения наблюдаются вблизи контактной поверхности. Скорость деформации
по длине и высоте очага такие же, как у распределения интенсивности деформации — от сечения входа к сечению выхода скорость деформации возрастает (от –0,07…–0,085 до –0,09…–0,115), а наибольшие значения наблюдаются вблизи контактной поверхности. Скорость деформации ![]() есть абсолютная величина среднего значения скоростей деформации в пределах всего очага и равна 1,73 1/с.
есть абсолютная величина среднего значения скоростей деформации в пределах всего очага и равна 1,73 1/с.
На рис. 3 показаны погрешности расчетов скорости деформации по различным формулам, приведенным в работе [1, с. 237]. Наименьшую погрешность 0,6 % дает вычисление по формуле А.И. Целикова, которая имеет следующий вид:
![]() ,
,
где: ![]() — окружная скорость рабочих валков.
— окружная скорость рабочих валков.
Малые погрешности (не более 5 %) наблюдаются также при использовании формул: В. Тринкса (3) , А.А. Королева (5), Д.И. Старченко (6), Р. Симса (7), В.Н. Выдрина (9).
(![]() ) (3)
) (3)
(![]() ) (4)
) (4)
( ) (5)
) (5)
(![]() ) (6)
) (6)
(![]() ) (7)
) (7)
Для оценки средней температуры ![]() исследовали распределение температуры по длине и высоте очага деформации. На рис. 4 в качестве примера показаны распределения
исследовали распределение температуры по длине и высоте очага деформации. На рис. 4 в качестве примера показаны распределения ![]() по высоте очага деформации вблизи сечений входа и выхода.
по высоте очага деформации вблизи сечений входа и выхода.

Рисунок 4. Распределение температуры по высоте очага вблизи сечения входа (а) и выхода (б)
При прохождении металла через очаг деформации его температура металла от 1200—1210 до 1175—1195 °С. Наибольшая температура наблюдается в середине полосы, причем градиент температуры по толщине вблизи сечения выхода (около 25 °С) заметно больше, чем на входе в очаг деформации (10 °С). Среднее значение температуры в очаге деформации равно 1195 °С. При расчетах сопротивления деформации в качестве температуры деформирования принимают температуру металла на входе в очаг деформации [1, с. 240]. Для рассматриваемого случая замена средней температуры по очагу деформации температурой на входе в него дает погрешность 5—15 °С, т. е. не более 2 %.
Таким образом, была поставлена и реализована в программном комплексе DEFORM 3D задача оценки усредненных значений температуры, степени и скорости деформации при горячей листовой прокатке. Выявлены известные формулы, которые для рассматриваемых условий дают наименьшие погрешности расчета степени и скорости деформации. Также установлено, что для рассматриваемых условий замена средней в очаге деформации температуры металла температурой на входе в очаг допустима и привносит погрешность не более 2%. Далее разработанная конечно-элементная модель и методика анализа получаемых результатов будут применяться в исследовании по выявлению формул, дающих наименьшие погрешности средних значений термомеханических параметров для других условий горячей листовой прокатки. По результатам данного исследования будут сформулированы рекомендации по применению тех или иных известных формул в зависимости от условий процесса прокатки.
Список литературы:
1.Зайков М.А., Полухин В.П., Зайков А.М., Смирнов Л.М. Процесс прокатки. М.: «МИСИС», 2004. — 640 с.
2.Коновалов Ю.В., Остапенко А.Л., Пономарёв В.И. Расчёт параметров листовой прокатки. М.: Металлургия, 1986. — 430 с.
3.Shiro Kobayashi, Soo-Ik Oh, Taylan Altan. Metal Forming and the Finite Element Method. New York, Oxford «Oxford University Press», 1989. — 198 p.
дипломов


Оставить комментарий