ПОНЯТИЕ  КОЭФФИЦИЕНТА  ФОРМЫ.  СУЩНОСТЬ  МЕТОДА  ИНТЕРПОЛЯЦИИ  ПО  КОЭФИЦИЕНТУ  ФОРМЫ  И  ИСПОЛЬЗОВАНИЕ  МЕТОДА  ДЛЯ  ОПРЕДЕЛЕНИЯ  ПРОГИБОВ  ПЛАСТИНОК

Бобков  Евгений  Александрович

студент  4  курса,  кафедра  ГСиХ  ГУУНПК,  РФ,  г.  Орел

Моисеева  Анастасия  Ивановна

Шляхов  Станислав  Владимирович

студенты  4  курса,  кафедра  СКиМ  ГУУНПК,  РФ,  г.  Орел

E -mail:  gbobkov93@mail.ru

Коробко  Виктор  Иванович

научный  руководитель,  д-р  тех.  наук,  профессор  ГУУНПК,  РФ,  г.  Орел

Для  сравнения  геометрических  фигур  различных  форм  необходим  некоторый  геометрический  критерий.  Фигуры,  относящиеся  к  одному  классу  форм,  сравниваются  с  помощью  коэффициента  подобия  (гомотетии).  Фигуры  в  пределах  одного  класса  простых  форм  могут  сравниваться  по  определяющему  их  параметру.  При  сравнении  же  фигур  различных  классов  простых  форм  возникают  трудности  в  выборе  критерия  сравнения.

Рассмотрим  произвольную  выпуклую  область  (рисунок  1)  и  зададимся  уравнением  ее  контура  в  полярных  координатах  r  =  r(φ).  Выберем  внутри  области  точку  «а»  и  опустим  из  нее  перпендикуляр  h  на  касательную,  проведенную  к  переменной  точке  контура  области.  Интеграл,  взятый  по  периметру  заданной  области,  является  количественной  характеристикой  формы  области  и  называется  коэффициентом  формы:

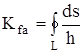  (1)

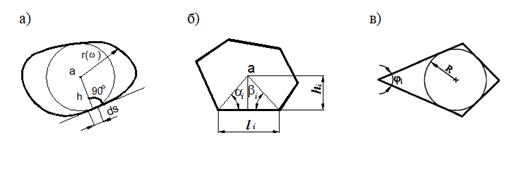
Рисунок  1.  К  определению  коэффициента  формы

Основные  свойства  коэффициента  формы:

1.  K_f  —  величина  безразмерная  и  не  зависит  от  масштаба  фигур.

2.  K_f  дает  количественную  оценку  формы  геометрических  фигур  с  выпуклым  контуром  и  может  служить  критерием  для  оценки  их  «правильности»  («симметричности»):  чем  меньше  K_f,  тем  более  «правильнее»  фигура.

3.    Любая  фигура  с  выпуклым  контуром  имеет  внутри  области  такую  единственную  точку  «а»  (центр  полярной  системы  координат),  которая  обеспечивает  минимальное  значение  коэффициенту  формы.

4.  Для  фигур,  имеющих  центр  симметрии,  точка  «a»,  обеспечивающая  minK_fa,  совпадает  с  этим  центром;  для  фигур,  имеющих  одну  ось  симметрии,  точка  «a»  лежит  на  этой  оси.

Существует  ряд  теорем  о  коэффициенте  формы  для  выпуклых  фигур.  Графическое  представление  этих  теорем  показано  на  рисунке  2

Рисунок  2.  Графическое  представление  границ  изменения  коэффициента  формы  для  всего  множества  выпуклых  фигур

В  монографии  А.В.  Коробко  [1,  с.  49]  после  интегрирования  дифферен-циального  уравнения  поперечного  изгиба  пластинок  по  всей  площади  было  получено  следующее  выражение  для  определения  максимального  прогиба  w₀:

,                                    (2)

где  D  —  цилиндрическая  жесткость  пластинки;  q(x;  y)  —  интенсивность  равномерно  распределенной  нагрузки;  f(x;  y)  —  единичная  функция  прогибов  из  выражения  w(x;  y)  =  w₀f(x;  y),  удовлетворяющая  условию  1  ≥  f(x;  y)  ≥  0;

Δ  —  оператор  Лапласа.

После  математических  преобразований  выражение  (2)  можно  приближенно  представить  в  виде  равенства:

,                                    (3)

где:  k  —  коэффициент  пропорциональности,  зависящий  от  формы  пластинки  и  ее  граничных  условий.

На  основании  известных  решений  по  определению  максимального  прогиба  при  поперечном  изгибе  от  действия  равномерно  распределенной  по  всей  площади  нагрузки  q  для  пластинок  простых  форм  с  шарнирным  опиранием  и  жестким  защемлением  контура  были  построены  кривые  «максимальный  прогиб  —  коэффициент  формы»  (рисунок  3).

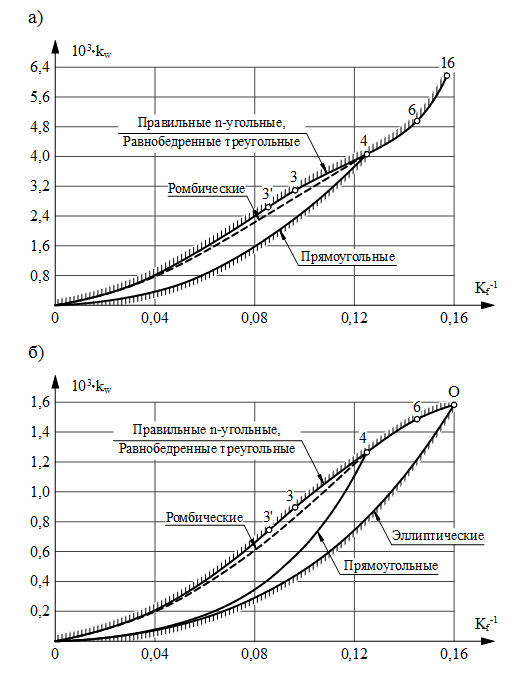
Рисунок  3.  Кривые  «максимальный  прогиб  k_w   —  коэффициент  формы  K_f»:  а)  шарнирное  опирание;  б)  жесткое  защемление

На  рисунке  3  точкам  3,  4,  6,  16  соответствуют  правильные  3-х,  4-х,  6-ти,  16-ти-угольные  пластинки;  точке  3'  —  равнобедренная  прямоугольная  треугольная  пластинка;  точке  O  —  круглая  пластинка.  Кривая  3-4-6-16(O)  объединяет  решения  для  правильных  n-угольных  пластинок,  кривая  0-3'-3  —  решения  для  равнобедренных  треугольных  пластинок.

Пусть  для  заданной  пластинки  с  выпуклым  опорным  контуром  требуется  определить  максимальный  прогиб  при  поперечном  изгибе  от  действия  равномерно  распределенной  нагрузки.  Если  удастся  подобрать  такое  геометрическое  преобразование  ее  формы,  при  котором  получатся  хотя  бы  две  пластинки  («опорные»  пластинки),  решения  для  которых  известны  («опорные»  решения),  либо  их  можно  получить  каким-либо  другим  методом,  то  искомое  решение  может  быть  найдено  путем  интерполяции  «опорных»  решений  по  коэффициенту  формы.  Этот  прием  получения  решений  был  предложен  А.В.  Коробко  и  составляет  сущность  метода  интерполяции  по  коэффициенту  формы.

Чтобы  не  ограничиваться  известными  в  справочной  и  научной  литературе  решениями  и  (или)  не  получать  для  каждого  случая  «опорные»  решения  другими  методами,  удобно  построить  аналитические  зависимости  «максимальный  прогиб  —  коэффициент  формы»  для  пластинок  некоторых  простых  форм,  из  которых  могут  быть  получены  заданные  пластинки.

При  выборе  геометрических  преобразований  следует  стремиться  к  тому,  чтобы  «опорные»  решения  в  координатных  осях  «максимальный  прогиб  —  коэффициент  формы»  отстояли  друг  от  друга  на  небольшом  расстоянии  с  целью  получения  искомых  решений  с  большей  точностью. 

Для  параллелограммов  и  трапеций  на  графиках  1/  существуют  экстремумы,  в  результате  чего  искомые  решения,  получаемые  из  линейной  и  степенной  зависимостей    находятся  с  большой  погрешностью.  Решение  этой  проблемы  предложил  Прокуров  М.Ю.:  графики  1/  и    являются  подобными;  составив  пропорцию  и  решив  ее,  можно  определить  прогиб  пластинки  с  более  высокой  точностью.

Покажем  это  на  примере  расчета  параллелограммной  пластинки.  Исходные  данные  приняты  следующими:  q  =  1  кН/м²,  толщина  пластинок  t  =  10  мм,  Е  =  206000  МПа,  υ  =  0,3.  Опирание  пластинок  —  шарнирное.

Тестовые  расчеты  выполнялись  в  программе  KfDeflection,  где  использовалась  нелинейная  интерполяция  решений:  при  ,  а  также  по  SCAD.  Прогибы  базовых  пластинок  вычислялись  по  подобранным  функциям  в  программе  KfDeflection.  Интерполяция  решения  предложенным  способом  выполнялась  вручную.

Геометрическое  преобразование  показано  на  рисунке  4,  при  a/b  =  2  (а  =  1  м,  b  =  0,5  м).

Базовая  прямоугольная  пластинка:  K_f  =  10,970;  1/K_f  =  0,0912;    =  0,0206  мм.

Ромбическая  пластинка:  K_f  =  18,474;  1/K_f  =  0,0541;    =  0,01296  мм.

Параллелограмм:  K_f  =  11,547;  1/K_f  =  0,0866;  определим  w.

Рисунок  4.  Геометрическое  преобразование

Строим  графики,  отражающие  геометрическое  преобразование  K_f  =  f(Ф)  и  соответствующее  изменение  значения  максимального  прогиба  w  =  f(Ф),  где  Ф  —  параметр,  варьируемый  при  используемом  преобразовании.  В  данном  случае  это  острый  угол  α,  изменяющийся  от  25,66°  до  90°.

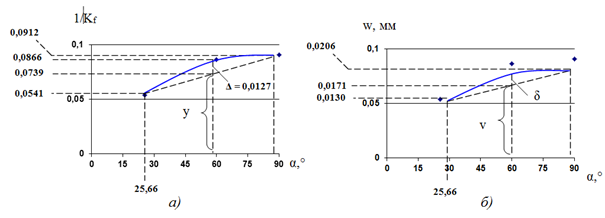
Рисунок  5.  Графики:  а)  K_f   =  f();  б)  w  =  f().

По  базовым  решениям  путем  линейной  интерполяции  определяются  значения:  у,  Δ,  v  (показаны  на  графиках  (рисунок  5).  Из  пропорции  Δ/у  =  δ/v  находим:

δ  =  vΔ/у  =  0,0171*0,0127/0,0739  =  0,0029.

Искомый  прогиб  равен:

w  =  v  +  δ  =  0,0171+  0,0029  =  0,02  мм.  (0,01998  мм).

По  программе  KfDeflection  w  =  0,01970  мм.

По  SCAD  w  =  0,020056  мм  (441  узел,  800  элементов).

Результаты  тестовых  расчетов  прогибов  показаны  в  таблице  1.

Таблица  1.

Результаты  тестовых  расчетов  прогибов

Для  трапецеивидных  пластинок  ход  решения  аналогичен  как  и  для  параллелограммных.

Представляется,  что  предложенный  подход  определения  прогиба  можно  было  бы  использовать  при  любой  форме  зависимости  K_f  =  f(Ф).

Список  литературы:

1.Расчет  пластинок  методом  предельного  равновесия  /  В.И.  Коробко,  А.В.  Коробко,  С.А.  Морозов,  М.Ю.  Прокуров  О.:  Типография  «Труд»,  2012.  —  360  с.

2.Черняев  А.А.  Разработка  теоретических  основ  метода  интерполяции  по  отношению  конформных  радиусов  для  решения  задач  поперечного  изгиба  пластинок.  Дисс.  канд.  техн.  наук.  О.,  2013.  —  280  с.