МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПРОГНОЗИРОВАНИЯ ДИНАМИКИ ПРЕСТУПЛЕНИЙ

Разработанная математическая модель прогнозирования динамики преступлений позволит прогнозировать количество преступлений на заданные периоды времени, что позволит сотрудникам Управления министерства внутренних дел своевременно принимать меры по обеспечению безопасности граждан, предупреждению и пресечению уголовных правонарушений за счет проведения профилактических мероприятий и бесед с гражданами, увеличения количества патрулей.

Данная система предназначена для внедрения в Управление министерства внутренних дел России. Пользователями системы будут сотрудники отдела информационного обеспечения штаба полиции.

На основании мнений группы экспертов получены следующие результаты: наибольшее влияние на значение количества преступлений соответствующей категории оказывают данные предшествующие прогнозируемому месяцу.

Прогнозирование динамики преступлений определяется по формуле:

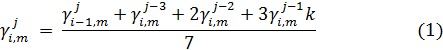
где  i – год; j – месяц;

m – показывает тяжесть преступления: m = 1 – небольшой тяжести; m = 2 – средней тяжести; m = 3 –тяжкое; m = 4 – особо тяжкое.

В формуле (1) прогнозируемые данные с учетом сезонных колебаний основываются на значениях данного месяца за предыдущий год, и данных по количеству преступлений текущего года, но за предшествующие месяцы оцениваемого периода.

В формулу (1) введен коэффициент, учитывающий повышение уровня преступности после амнистии – k. Если амнистия произошла в (j-1) месяце, то в следующем месяце ожидается повышение количества совершенных преступлений небольшой и средней тяжести: k = 1,75;  k = 1,5; k = 1,25. Увеличение количества тяжких и особо тяжких преступлений не связано с актом об амнистии, так как акт об амнистии не распространяется на лиц, совершивших тяжкие или особо тяжкие преступления, а также наказание которым назначено при опасном или особо опасном рецидиве преступлений [4].

 Понижение коэффициента k происходит за счет трудоустройства амнистированных, либо повторного  возбуждения уголовного дела против них за совершение преступлений.

Статистика по кварталам, определяется по общей формуле:

                   (2)

где l – номер квартала, при l=1, j= 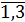 , т.е. первому кварталу соответствуют первые три месяца, следовательно, l = 2, j = 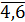; l = 3, j = 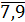, l=4, j= .

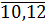Прогноз текущего года на следующий квартал определяется, по формуле:

Была проведена оценка адекватности математической модели, в среднем отклонение составило не более 6%.

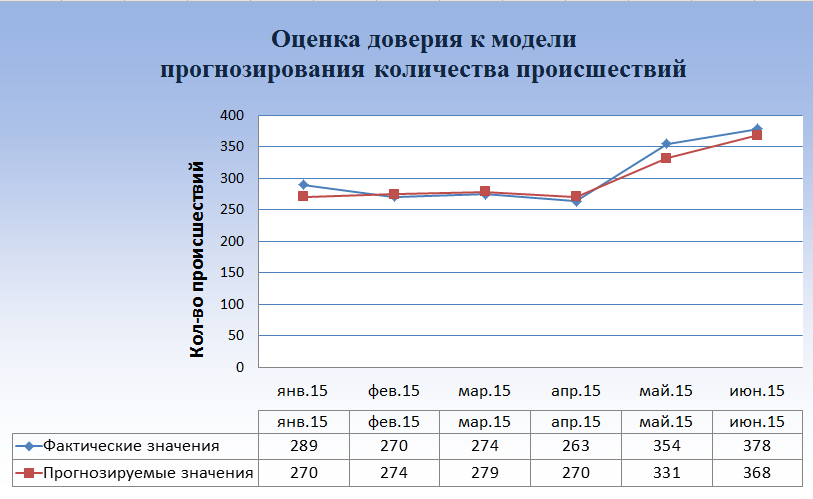
Рисунок 1. Сравнение прогнозируемых значений с фактическими значениями

Для сравнения было проведено прогнозирование с помощью регрессионного анализа. Регрессионный анализ – статистический метод исследования влияния одной или нескольких независимых переменных            x₁, x₂, ...,x_p  на зависимую переменную Y. Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные – критериальными [3].

Регрессионный анализ заключается в определении аналитической формы связи, в которой изменение результативного признака обусловлено влиянием одного или нескольких факторных признаков, а множество всех прочих факторов, также оказывающих влияние на результативный признак, принимается за постоянные и средние значения [1].

Уравнение регрессии записывается в виде:

               Y=b₀+b₁x₁+b₂x₂+b₃x₃+b₄x₄+b₅x₅                               

где x₁ – количество преступлений данного месяца за предыдущий год;   x₂, x₃, x₄  – количество преступлений текущего года, но за предшествующие месяцы оцениваемого периода; x₅  – количество амнистий.

Так как количество факторов влияющих на y равно 5, то потребуется 2^k опытов, где k=5.

Каждый b_i-ый член уравнения регрессии (4) определяется по формуле:

b_i=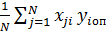   (5)

После проведения расчетов, получается следующее уравнение регрессии, с помощью которого рассчитываются прогнозируемые значения:

                            Y=280+4,1x₁-10,7x₂ +5,5x₃ -14,3x₄ +1,5x₅    (6)   

Была проведена оценка адекватности математической модели с использованием регрессионного анализа, в среднем отклонение составило не более 21%.

Кроме того было проведено прогнозирование динамики преступлений с учетом таких факторов как: количество амнистий, количество населения, количество праздничных дней в году, количество притока населения.

Уравнение регрессии записывается в виде:

                         Y = b₀+b₁x₁ +b₂x₂ +b₃x₃ +b₄x₄ +b₁₂x₁x₂ + b₂₄x₂x₄     (7)   

где x₁ – количество амнистий;  x₂– количество населения;  x₃– количество праздничных дней в году;  – количество притока населения.

В данном случае отклонение прогнозируемых значений от фактических данных составило около 43%.

Существенным недостатком регрессионного анализа является то, что прогнозируемый период зависит от количества факторов, на основе которых составляется исходное уравнение регрессии.

Прогнозирование помогает формулированию целей и задач борьбы с преступностью на соответствующий период и планированию деятельности по их осуществлению, в том числе по предупреждению преступности. При этом речь идет не просто о том, чтобы «приспособить» эту деятельность к ожидаемому состоянию объекта воздействия, а о том, чтобы максимально стимулировать благоприятные для общества тенденции преступности (снижение уровня, смягчение структуры) и предупредить или максимально ослабить возможные в определенный период и на определенной территории обратные тенденции [2].

  Прогнозирование динамики преступлений является обязательной предварительной стадией планирования борьбы с преступностью и позволяет найти в ходе его выполнения оптимальные решения.

Список литературы:

1.   Лекционный материал для студентов: сайт – [Электронный ресурс]  –  Режим доступа. – URL: http://studopedia.ru/2_34939_sushchnost-analiza-uravnenie-regressii-metod-naimenshih- kvadratov.html (дата обращения: 07.07.2016).

2.   Учебный портал РУДН: сайт – [Электронный ресурс]  – Режим     доступа. – URL: http://web-local.rudn.ru/web-local/uem/ido/krim/P8.htm      (дата обращения: 07.07.2016).

3.   Энциклопедия Википедия: сайт – [Электронный ресурс] – Режим доступа.URL:https://ru.wikipedia.org/wiki/Регрессионный_анализ (дата обращения: 07.07.2016).

4.   Энциклопедия «Экономиста!»: сайт – [Электронный ресурс] – Режим доступа.–URL:http://www.grandars.ru/college/pravovedenie/amnistiya.html  (дата обращения: 07.07.2016).