ОПЕРАЦИОННОЕ  ИСЧИСЛЕНИЕ  В  ЭЛЕКТРОТЕХНИКЕ

Симонович  Денис  Алексеевич

студент  2  курса,  кафедры  электроэнергетики  и  электротехники  ДВФУ,  г.  Владивосток

E-mail:  cimonovich@list.ru

Дмух  Галина  Юрьевна

научный  руководитель,  канд.  пед.  наук,  доцент  кафедры  алгебры,  геометрии  и  анализа,  ДВФУ,  г.  Владивосток

Операционное  исчисление  является  эффективным  аппаратом  исследования  многих  теоретических  вопросов  и  прикладных  задач,  как  в  самой  математике,  так  и  в  других  областях  науки  и  техники,  особенно  тех  вопросов  и  задач,  которые  связанны  с  решением  линейных  дифференциальных  уравнений.  В  частности,  операционное  исчисление  применяется  при  исследовании  многих  вопросов  и  задач  физики,  механики,  теории  автоматического  регулирования,  электротехники,  радиотехники,  теплопроводности,  горной  техники  [3.  с.  3].

Суть  операционного  исчисления  заключается  в  следующем:  функциям,  удовлетворяющим  некоторым  условиям  (пространство  оригиналов)  соответствуют  функции  в  другом  пространстве  (пространстве  изображений)  так,  что  интегрированию  и  дифференцированию  в  пространстве  оригиналов  соответствуют  более  простые  операции  (умножения  и  деления)  в  пространстве  изображений.  Затем  дифференциальное  уравнение  в  пространстве  оригиналов  преобразуется  в  алгебраическое  уравнение  в  пространстве  изображений,  решение  которого  значительно  упрощается.  Завершающим  действием  является  восстановление  решения  уравнения  по  его  изображению. 

Операционное  исчисление  в  электротехнике  применяется  при  расчете  переходных  процессов  в  линейных  цепях  с  постоянными  параметрами  r  (сопротивление)  ,  L  (индуктивность)  и  C  (электроемкость),  так  как  линейные  дифференциальные  уравнения  и  их  системы,  которыми  описываются  процессы  в  этих  цепях,  легко  решаются  методом  операционного  исчисления. 

Переходным  процессом  называется  переход  от  одного  режима  работы  электрической  цепи  к  другому,  чем-либо  отличающемуся  от  предыдущего.  Эти  процессы,  как  правило,  вызваны  коммутацией  в  цепи  (замыканием  или  размыканием  выключателей).  Данное  явление  происходит  мгновенно,  при  этом  не  исключены  случаи,  когда  при  переходном  процессе  значительно  увеличиваются  значения  напряжения  и  токов  в  цепи  или  на  отдельных  ее  элементах  относительно  установившегося  режима,  в  результате  чего  может  выйти  из  строя  электрическое  оборудование.

При  любых  переходных  и  процессах  соблюдают  два  основных  положения:  ток  через  индуктивность  и  напряжение  на  емкости  не  могут  изменяться  скачком.  Отсюда  следуют  два  закона  (правила  коммутации):

1.                     Ток  через  индуктивность  непосредственно  до  коммутации    (0-)  равен  току  через  туже  индуктивность  непосредственно  после  коммутации    (0+):

.

2.  Напряжение  на  емкости  непосредственно  до  коммутации  (0-)  равно  напряжению  на  емкости  непосредственно  после  коммутации  (0+):

(0+)  =  (0-)  =  (0)  .

При  расчете  переходного  процесса  в  электрической  цепи,  прежде  всего,  нужно  выявить  значения  токов  в  индуктивностях  и  напряжений  на  обкладках  конденсаторов  в  момент  времени,  предшествующий  коммутации  в  цепи,    (0)  и    (0)  —  начальные  условия  переходного  процесса.  Если  все  значения    (0)  и  (0)  равны  нулю,  то  токи  в  индуктивностях  и  напряжения  на  конденсаторах  в  переходном  процессе  начнут  изменяться  от  нулевых  значений.  Для  определения  знаков  при  ненулевых  начальных  условиях    (0)  и  (0)  необходимо  определить  направления  обхода  контуров  цепи,  в  которых  происходит  переходный  процесс.  Если  направления    (0)  и    (0)  совпадают  с  направлением  обхода  контура  то  сохраняются  положительные  знаки,  иначе  знаки    (0)  и  (0)  изменятся  на  противоположные.  В  этом  случае  значения  токов  в  индуктивностях  и  напряжения  на  конденсаторах  в  переходном  процессе  будут  меняться  от  значений,  которые  они  имели  непосредственно  перед  коммутацией  (с  учетом  полученных  знаков  этих  величин).

Пусть  в  электрической  цепи  (рис.  1),  ключ  P  переходит  из  положения  1  в  положение  2.  В  этом  случае  возникнет  переходный  процесс.  Допустим,  что  начальные  условия  переходного  процесса  ненулевые:    (0)  ≠  0  и    (0)  ≠  0  .  Следовательно,  при  заданном  направлении  тока  в  индуктивности  и  напряжении  на  обкладках  конденсатора  в  начальный  момент  переходного  процесса,  значения    (0)  и    (0)  больше  нуля.

Рисунок  1.  Электрическая  цепь

Пусть  направление  мгновенного  значения  тока  переходного  процесса  i  =  i(t),  и  источника  э.  д.  с.  e  =  e(t),  совпадают  с  направлением  обхода  контура.  Значит  по  второму  закону  Кирхгофа:

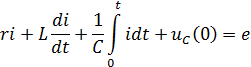
e(p)  =  e  =  E(p)  —  изображение  внешней  э.  д.  с.  ,  действующей  в  контуре;

i(p)  =  i  =  I(p)  —  изображение  тока  переходного  процесса  в  контуре.

В  этом  случае  уравнение  нашей  цепи  в  операторной  форме  примет  вид:

Данное  уравнение  можно  записать  как:

Далее  находим  выражение  изображения  тока  переходного  процесса:

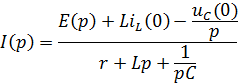
Это  уравнение  является  законом  Ома  в  операторной  форме:

где:    —  это  изображение  всех  (внешних  и  дополнительных)  э.  д.  с.  ,  действующих  в  нашем  контуре; 

  —  операторное  сопротивление  контура  ;

  —  изображение  начальной  э.  д.  с.  емкости,  которая  направлена  навстречу    и  уравновешивает  начальное  напряжение  на  обкладках  конденсатора.

Операторное  сопротивление  Z(p)  =  r  +  Lp  +    контура  r  ,  L  и  C  получено  из  выражения  полного  комплексного  сопротивления  данного  контура  Z  =  r  +  iwL  +    ,  заменив  iw  на  p  ,  =  −1  .

Благодаря  Закону  Ома  в  операторной  форме  можно  исследовать  переходные  процессы  только  в  неразветвленных  электрических  цепях.  Исследуя  переходные  процессы  в  сложных  или  разветвленных  электрических  цепях  нужно  применять  первый  и  второй  законы  Кирхгофа,  которые  в  операторной  форме  можно  записать  так:

Первый  закон  — 

Второй  закон  — 

При  составлении  уравнения  по  второму  закону  Кирхгофа,  нужно  принимать  во  внимание  то,  что  кроме  внешних  э.  д.  с.  в  контурах,  которые  содержат  индуктивности  и  емкости  не  равные  нулю,  действуют  также  внутренние  э.  д.  с.  (начальные  э.  д.  с.:  емкости  и  самоиндукции).  При  этом,  если  направление  сонаправлено  с  направлением  обхода  контура,  то  значение    берем  со  знаком  «плюс»,  если    также  направлено  по  обходу  контура,  тогда  результирующий  знак  значения    будет  «минус»,  так  как  начальная  э.  д.  с.  емкости  всегда  направлена  навстречу  начальному  напряжению  на  обкладках  конденсатора  .

В  операторной  форме  законы  Ома  и  Кирхгофа  записываются  так  же,  как  и  в  цепях  переменного  и  постоянного  тока  с  постоянными  режимами.  Именно  поэтому,  при  применении  операционного  исчисления  в  расчетах  переходных  процессов,  можно  использовать  любые  методы  вычисления  сложных  линейных  электрических  цепей  с  постоянными  параметрами.  Метод  уравнений  Кирхгофа,  метод  контурных  токов  и  метод  наложения  получили  наибольшее  применение  при  исследовании  переходных  процессов  в  сложных  и  разветвленных  электрических  цепях.  Закон  Ома  в  операторной  форме  используется  при  расчете  переходных  процессов  в  неразветвленных  цепях,  а  также  в  простых  разветвленных  цепях  при  нулевых  начальных  условиях.  Причем  в  разветвленной  цепи  определяется  только  ток  переходного  режима  в  ветви,  содержащей  источник  э.  д.  с.

При  расчете  переходных  процессов  в  электрических  цепях  операторным  методом  существует  следующая  последовательность  действий:  сперва  определяются  начальные  условия,  после  чего  записывается  уравнение  или  система  уравнений  для  данной  цепи  в  операторной  форме,  благодаря  чему  можно  найти  изображения  искомых  токов  или  напряжений.  Затем,  по  найденным  изображениям  определяются  оригиналы  —  мгновенные  значения  токов  или  напряжений  переходного  процесса.

Список  литературы:

1.Бессонов  Л.А.  Теоретические  основы  электротехники:  Электрические  цепи:  Учебник  для  студентов  электротехнических,  энергетических  и  приборостроительных  специальностей  вузов.  —  7-е  изд.,  перераб.  и  доп.  М.:  Высш.  школа,  2008.  —  528  с. 

2.Мацкевич  И.Ю.  Высшая  математика:  приложения  в  физике  и  электронике:  учеб.-метод.  пособие  для  учащихся  специальностей  2-39  02  02  «Проектирование  и  производство  радиоэлектронных  средств»,  2-39  02  31  «Техническая  эксплуатация  радиоэлектронных  средств»,  2-40  02  02  «Электронные  вычислительные  средства»,  2-41  01  31  «Микроэлектроника»  /  И.Ю.  Мацкевич.  Мн.:  МГВРК,  2008.  —  124  с.

3.Штокало  И.З.  Операционное  исчисление  (Обобщения  и  приложения)  Издательство  «Наукова  Думка»  Киев  1972.  —  279  с.