ПРИМЕНЕНИЕ  ГЕНЕТИЧЕСКОГО  АЛГОРИТМА  ДЛЯ  ПОСТРОЕНИЯ  ИНДИВИДУАЛЬНОГО  МАРШРУТА  КОНТРОЛЯ  ЗНАНИЙ  СТУДЕНТА  В  СЕТЕВОЙ  ИНФОРМАЦИОННОЙ  СИСТЕМЕ

Томилова  Наталья  Александровна

студент  2  курса  магистратуры  Тюменского  Государственного  Нефтегазового  Университета,  г.  Тюмень

Email:  tomilova_nafanya@mail.ru

Шалкина  Татьяна  Николаевна

научный  руководитель,  канд.  пед.  наук,  доцент  Тюменского  Государственного  Нефтегазового  Университета,  г.  Тюмень

Email:  shalkina-tn@yandex.ru

Контроль  знаний  —  одна  из  актуальных  проблем  современного  профессионального  образования.  Несмотря  на  большое  количество  публикаций  по  этой  проблеме,  к  вопросам,  которые  недостаточно  проработаны,  можно  отнести  контроль  и  оценку  уровня  сформированности  профессиональных  компетенций  студента  в  процессе  обучения. 

Анализ  популярных  систем,  используемых  в  современном  дистанционном  обучении,  таких  как  WebCT  ,  BlackBoard,  Desire2Learn,  Moodle,  Sakai  [1,  2,  3,  4],  показал,  что  обычно  учебный  курс  представляет  собой  набор  статических  гипертекстовых  документов.  Все  студенты  получают  одинаковый  материал  для  изучения  и  сходные  задания  контроля  приобретенных  знаний,  умений  и  навыков  без  учета  их  индивидуальных  особенностей.  Наиболее  востребованным  видом  компьютерного  контроля,  нашедшим  применение  в  оценке  знаний  и  умений  студентов,  является  компьютерное  тестирование.  При  всех  положительных  моментах  компьютерного  тестирования,  этот  метод  не  позволяет  в  полной  мере  оценить  все  заявленные  в  образовательных  стандартах  компетенций.

Учитывая  вышесказанное,  отметим,  что  методика  проведения  контроля  в  условиях  компетентностно-ориентированной  образовательной  программы:

·должна  быть  максимально  гибкой,  учитывающей  индивидуальные  способности  и  профессиональные  интересы  студента;

·должна  давать  возможность  студенту  выбора  индивидуального  обучающего  маршрута  на  основе  имеющегося  у  него  личностного  и  профессионального  опыта.

Задача  построения  индивидуального  маршрута  сводится  к  выбору  последовательности  обучающих  заданий,  которая  отвечает  следующим  условиям:

·общая  временная  протяженность.  Общее  время,  которое  потребуется  затратить  на  выполнение  заданий;

·значимость  задания.  Определяет  минимальный  значение  значимости  (важности),  которое  должно  иметь  задание  для  включения  в  маршрут.

Для  различных  вариантов  маршрутов  обучения  необходимо  ввести  критерии  сравнения:

·     коэффициент  удовлетворения  потребностей;

·     среднее  значение  значимости.

Для  поставленной  задачи  предлагается  использовать  механизм  генетических  алгоритмов  (ГА),  которые  предназначены  для  решения  задач  оптимизации.  ГА  работают  с  совокупностью  особей  —  популяцией,  каждая  из  которых  представляет  возможное  решение  данной  проблемы.  Каждая  особь  оценивается  мерой  ее  приспособленности  согласно  тому,  насколько  хорошо  соответствующее  ей  решение  задачи.  Наиболее  приспособленные  особи  получают  возможность  воспроизводить  потомство  с  помощью  перекрестного  скрещивания  с  другими  особями  популяции.  В  конечном  итоге  популяция  будет  сходиться  к  оптимальному  решению  задачи.

Под  популяцией  будем  понимать  конечное  множество  вариантов  перечней  образовательных  компонентов.  В  соответствии  с  введенными  ранее  обозначениями  популяция  описывается  совокупностью:

,

где:  n  —  численность  популяции.

Особи,  входящие  в  популяцию,  в  генетических  алгоритмах,  представляются  хромосомами,  с  закодированными  в  них  множествами  параметров  задачи.  В  терминах  рассматриваемой  задачи  особями  являются  варианты  маршрутов  заданий  Tⁱ.  Каждый  перечень  Tⁱ  характеризуется  определенным  составом  заданий,  который  выступает  в  роли  интересующего  нас  параметра.  Таким  образом,  каждая  особь  кодируется  единственной  хромосомой.  В  роли  генов  будем  рассматривать  только  те  задания,  которые  находятся  в  непосредственной  связи  с  компетенциями,  входящими  в  исследуемый  набор.

Совокупность  хромосом  особи  представляют  собой  генотип.  В  свою  очередь,  набор  значений,  т.е.  декодированная  структура,  соответствующая  генотипу  называется  фенотип.  В  качестве  фенотипа  выступает  структура:

,

где:  p  —  число  заданий,  входящих  в  перечень  .

Для  представления  генотипа  предлагается  использовать  двоичное  кодирование  хромосомы  особи.

Для  оценки  каждой  особи  в  популяции  необходимо  задать  функцию  приспособленности.  Поскольку  решаемая  задача  является  многокритериальной,  то  и  функций  приспособленности  будет  несколько.  В  этом  случае  необходимо  найти  некоторый  компромисс,  в  роли  которого  выступает  решение,  оптимальное  в  смысле  Парето.  Для  нахождения  такого  компромисса  воспользуемся  подходом,  предложенным  в  работе  [5,  с.  167].  Согласно  данному  подходу  особь,  являющаяся  лидером  в  данной  популяции,  определяется  по  формуле:

,

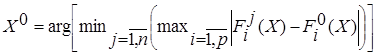где:  n  —  численность  популяции, 

p  —  количество  оптимизируемых  функций, 

  —  значение  i-ой  функции  приспособленности  для  j-ой  особи, 

—  наилучшее  значение  i-ой  функции  среди  всех  особей  популяции.

Таким  образом,  лучшей  будет  та  особь  популяции,  которая  имеет  наименьшее  среди  наибольшего  отклонения  от  лучшего  значения  функций  приспособленности  в  популяции.

Когда  задача  сформулирована  в  терминах  генетического  алгоритма,  можно  приступить  к  его  реализации.  Схема  работы  ГА  приведена  на  рисунке  1.

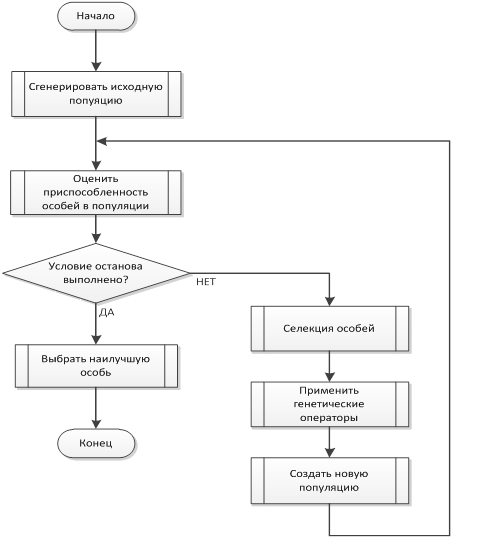
Рисунок  1.  Схема  работы  генетического  алгоритма

Результатом  работы  описанного  алгоритма  является  перечень  заданий  индивидуального  маршрута,  оптимальный  с  точки  зрения  заданных  ограничений.

Таким  образом,  используемый  алгоритм  призван  повысить  качество  подготовленности  студентов,  формировать  и  улучшать  навыки  студента,  за  счет  адаптивного  формирования  набора  заданий.

Список  литературы:

1.Официальный  сайт  Blackboard  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://www.blackboard.com  (дата  обращения  16.12.2012).

2.Официальный  сайт  Sakai  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://sakaiproject.org/  (дата  обращения  16.12.2012).

3.Официальный  сайт  Moodle  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://www.moodle.org  (дата  обращения  16.12.2012). 

4.Официальный  сайт  Desire2Learn  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://www.desire2learn.com  (дата  обращения  16.12.2012).

5.Рутковская  Д.,  Пилиньский  М.,  Рутковский  Л.  Нейронные  сети,  генетические  алгоритмы  и  нечеткие  системы:  Пер.  с  польск.  И.Д.  Рудинского.  —  М.:  Горячая  линия  —  Телеком,  2006.  —  452  c.