МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ СПЛОШНЫХ ПОСТОЯННЫХ МАГНИТОВ ДВУХКООРДИНАТНЫХ МАГНИТОСТРИКЦИОННЫХ НАКЛОНОМЕРОВ

Зюзина Елена Григорьевна

студент 5 курса, ФИОТ, ПГТА, г. Пенза

Е-mail: 

">

Володин Василий Анатольевич

студент 4 курса, ФИОТ, ПГТА, г. Пенза

Е-mail: Yahuu92@mail.ru

Слесарев Юрий Николаевич

научный руководитель, д-р техн. наук, профессор каф. «Автоматика и управление» ПГТА, г. Пенза

Воронцов Александр Анатольевич

научный руководитель, аспирант каф. «Физика» ПГТА, г. Пенза

В настоящее время во многих видах промышленности для определения углов наклона объекта относительно горизонтали или вертикали все чаще используют различные виды наклономеров. По ряду основных параметров, таких как точность, стоимость, масса, габариты и быстродействие [1—3] привлекательными являются магнитострикционные наклономеры (МН). В зависимости от области применения, МН подразделяют на два основных класса: однокоординатные и двухкоординатные МН (ДМН). Последние позволяют одновременное определение углов наклона относительно горизонтали или вертикали в двух взаимно перпендикулярных плоскостях.

Одной из перспективных разновидностей ДМН, из-за отсутствия в них дисперсии скорости, является ДМН с использованием ультразвуковых волн (УЗВ) кручения.

В качестве объекта исследования выберем один из вариантов ДМН на УЗВ кручения, схема которого приведена на рис. 1.

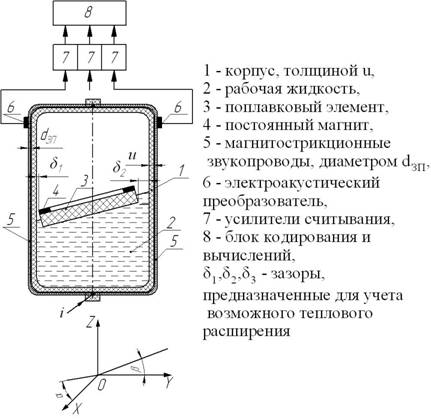
Рисунок 1. — Структурная схема ДМН на УЗВ кручения

Следует отметить, что результирующее магнитное поле, формируемое ДМН, состоит из двух составляющих — созданной токовым импульсом при протекании им в среде звукопровода (ЗП) и созданной постоянным магнитом (ПМ). Последняя составляющая представляет наибольший интерес, так как она зависит от множества факторов, основными из которых являются форма и размеры ПМ, а также значение остаточной намагниченности  и коэрцитивной силы .

Задачей данной статьи является оценка влияния каждого из основных факторов, влияющих на формирование магнитного поля созданных сплошным (СПМ) ПМ, используемого в ДМН методом математического моделирования. Это позволит улучшить характеристики ДМН и снизить его себестоимость.

Одним из способов аналитического преобразования уравнений магнитного поля является их предварительное сведение к уравнению относительно скалярного магнитного потенциала [4]. Данный метод расчета является наиболее эффективным, так как скалярными здесь являются не только рассчитываемая величина, но и решаемое уравнение в целом.

Для моделирования магнитных полей, созданных сплошным ПМ, выведем соответствующую формулу расчета с учетом влияния перечисленных факторов указанным методом применительно к различным конструкциям ДМН.

Известно, что напряженность магнитного поля , созданного фиктивными поверхностными зарядами сплошного ПМ с плотностью , согласно рисунку 2, определяется по формуле [5]

,                                 (1)

где:  — элементарный магнитный момент;

 — вектор, направленный из точки A(x,y,z), расположенной на верхней или нижней поверхности ПМ в точку B(), расчета напряженности магнитного поля;

 — единичный вектор в направлении .

Элементарный магнитный момент  можно рассчитать согласно [5] по формуле

,                     (2)

где:  — нормаль к плоскости ПМ,

 — вектор намагниченности,

 — элементарная площадь ПМ.

C учетом того, что косинус угла  между векторами и согласно рисунка 2, можно записать как , формулы (2), а также, что , , напряженность магнитного поля  из (1) определится выражением:

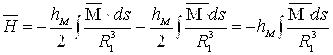,          (3)

где:  — высота ПМ.

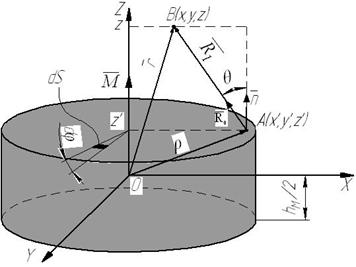
Рисунок 2 Поясняющий рисунок к расчету магнитного поля ПМ цилиндрической формы

Так как проекции векторов намагниченности и напряженности магнитного поля на ось Z равны  и , то выражение (3) для проекции  можно записать:

                           (4)

В цилиндрической системе координат выражение (2.4) имеет вид:

,    (5)

где:  — расстояние от центра ПМ до точки расчета напряженности магнитного поля, ;

 — полярный радиус, определяемый расстоянием от центра ПМ до точки, лежащей на его верхней или нижней поверхности, ;

 — радиус ПМ.

Выражение (5) можно упростить, используя известное равенство [6]:

,                      (6)

где: и  — константы,

 — угол.

Окончательно, проекция вектора напряженности магнитного поля на ось Z, созданного ПМ радиусом  и высотой  будет рассчитываться:

,    (7)

где:  — полный эллиптический интеграл второго рода, .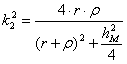

На основании формулы (7) можно сделать вывод, что напряженность магнитного поля, созданная ПМ в разной степени зависит от его размеров и величины остаточной намагниченности.

Это также наглядно демонстрируют результаты моделирования зависимостей напряженности магнитного поля, созданные сплошным ПМ от высоты (рисунок 3), диаметра  СПМ (рисунок 4) а также марки ПМ (рисунок 5). Для моделирования в качестве основного был выбран СПМ с размерами х=110х5 мм соответственно со значением остаточной индукции =0,3 Тл. Моделируемое значение напряженности определялось вдоль оси абсцисс, совмещенной с центром ПМ.

Рисунок 3 Зависимость напряженности магнитного поля от высоты СПМ

Анализ результатов моделирования, приведенных на рисунках 3—5, позволяет сделать вывод, что наиболее эффективным способом изменения напряженности магнитного поля вне ПМ является изменение значения остаточной индукции, определяемой маркой ПМ и высоты.

Изменение диаметра ПМ при значениях >5мм сопровождается незначительным изменением значения напряженности магнитного поля вне ПМ. Поэтому дальнейшее увеличение этого значения является необоснованным.

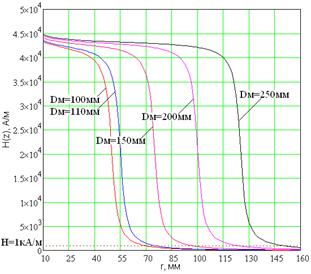
Рисунок 4 Зависимость напряженности магнитного поля от диаметра СПМ

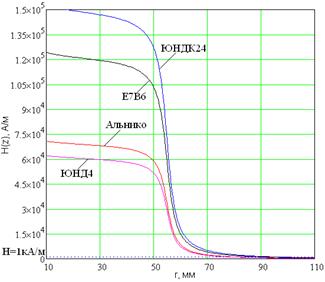
Рисунок 5 Зависимость напряженности магнитного поля от марки СПМ

Также необходимо отметить, что максимальное значение напряженности магнитного поля было зафиксировано в центре ПМ.

Таким образом, полученные в результате теоретического исследования математические формулы позволяют найти оптимальное значение параметров конструкции, что позволяет подобрать оптимальное значение массы и габаритов ДМН, уменьшая при этом его себестоимость изготовления.

Список литературы:

1.Воронцов А.А. Применение наклономеров в системах обеспечения безопас­ности автомобильных стрело­вых кранов / А.А. Воронцов, С.Б. Демин, Н.А. Ермолаев // Перспективные направления развития авто­транспортного комплекса: Сб. статей международной НПК. ― Пенза: ПГУАС, 2008. ― с. 36―39.

2.Воронцов А.А. Наклономеры в системах обес­печения безопасности строи­тельных работ / А.А. Воронцов, С.Б. Демин, Н.А. Ермолаев // Экология и безопасность жизнедеятель­ности: Сб. статей VIII международной НПК. ― Пенза: ПГСХА, 2008. ― с. 63―65.

3.Воронцов А.А. Наклономеры в автомобильных стреловых кранах / А.А. Воронцов, С.Б. Демин// Проблемы автомобильно-дорожного комплекса России: Сб. статей V международной НТК. ― Пенза: ПГУАС, 2009. ― с. 39―42.

4.Демирчян К.С., Чечурин В.Л. Машинные расчеты электромагнитных полей: Учеб. пособие для электротехн. и энерг. спец. Вузов. ― М.: Высш. шк., 1986. ― 240 с.

5.Brown W.F. Magnetostatic principles in ferromagnetism. ― N. Y.: North Holland Publishing Company, 1962. ― 202 p.

6.Huth B.G. Calculations of stable domain radii produced by termomagnetic writing// IBM J. Res. Develop. ― 1974. ― Vol. 18, № 2. ― P. 100―109.