Статья опубликована в рамках: VI Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 18 ноября 2012 г.)
Наука: Информационные технологии
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
«АНАЛИЗ ФОРФЕЙТНОЙ ОПЕРАЦИИ»
Скрипникова Нина Игоревна
студент 4 курса, факультет экономики и управления, ОГУ, г. Оренбург
Зеленина Татьяна Александровна
научный руководитель ассистент кафедры математических методов и моделей в экономике, ОГУ, г. Оренбург
В конце XX века человечество вступило в стадию развития, которая получила название постиндустриального или информационного. Возможности информационных технологий для человека становятся безграничными, способствуют эффективному решению профессиональных, экономических, а также многих других проблем. Информационные технологии значительно экономят время при проведении расчетов.
Одной из самых распространенных операций, проводимых банками, является форфейтной операция.
Сущность форфейтной операции [1, c. 305―306]
Название форфейтная операция или форфейтинг происходит от французского слова a forfait, что означает ― целиком, общей суммой.
Сущность форфейтирования заключается в следующем. Покупатель, не имеющий в момент заключения контракта необходимой суммы денег на оплату товара, выписывает продавцу комплект векселей на сумму, равную стоимости товара плюс проценты за отсрочку платежа. Сроки платежей равномерно распределяются во времени. Обычно оплата векселей предусматривается по полугодиям.
Продавец учитывает полученный комплект векселей в банке и сразу получает деньги за проданный товар. Таким образом, кредитором покупателя фактически оказывается банк, который согласился учесть комплект векселей и тем самым взял риск на себя. Степень риска сказывается на размере дисконтной ставки, по которой производится учет векселей.
Каждая из сторон, участвующих в форфейтной сделке, преследует собственные цели, которые учитываются при разработке условий контракта.
Цель продавца ― получить от банка после учета векселей сразу все деньги за проданный товар, устранив тем самым риск отказа покупателя от платежей.
Цель покупателя ― приобрести товар с минимальными издержками. Расходы покупателя заключаются в погашении последовательно предъявляемых ему банком векселей.
Цель банка ― получение дисконтного дохода от учета векселей.
Анализ форфейтной операции можно провести с позиции каждого из ее участников, однако при этом необходимо принимать во внимание интересы и других участников.
Анализ позиции продавца [1, c. 305―306]
Продавец получает деньги за проданный товар, учитывая в банке выданные покупателем векселя. Суммарная учетная цена векселей должна равняться стоимости товара. Таким образом, перед продавцом стоит задача определения необходимой стоимости каждого векселя.
Сумма ![]() , указанная на векселе (его номинальная стоимость), состоит из двух частей: суммы, погашающей основной долг (стоимость товара), и процентов за кредит. Проценты за кредит могут определяться двумя способами:
, указанная на векселе (его номинальная стоимость), состоит из двух частей: суммы, погашающей основной долг (стоимость товара), и процентов за кредит. Проценты за кредит могут определяться двумя способами:
a. проценты начисляются на остаток основного долга; в этом случае срок, за который они начисляются, начинается с момента погашения предыдущего векселя;
b. проценты начисляются на сумму долга, включенную в вексель; в этом случае срок определяется от начала сделки до момента погашения векселя.
Рассмотрим оба способа, полагая, что долг погашается равными выплатами. Введем обозначения:
― число выданных векселей или периодов выплат;
― ставка простых процентов за период, по которой производится кредитование;
![]() ― простая учетная ставка за период, используемая банком при учете векселей;
― простая учетная ставка за период, используемая банком при учете векселей;
― цена товара за вычетом аванса, если он имел место по условию сделки;
![]() ― число выплат в году по векселям.
― число выплат в году по векселям.
Вариант «а». Основной долг гасится равными выплатами ![]() . В сумму, подлежащую уплате по векселю, включаются также проценты за кредит на остаток основного долга. Эти процентные платежи образуют ряд, представляющий арифметическую прогрессию:
. В сумму, подлежащую уплате по векселю, включаются также проценты за кредит на остаток основного долга. Эти процентные платежи образуют ряд, представляющий арифметическую прогрессию:
![]()
где: ![]() ― номер периода.
― номер периода.
Сумма векселя, погашаемого в момент ![]() , равна
, равна
![]()
Общую сумму всех векселей находим как сумму членов этой арифметической прогрессии:
![]()
Наконец, общая сумма процентов за кредит равна
![]()
Вариант «б». Процентные платежи по периодам образуют теперь следующий ряд:
![]()
Сумма векселя, погашаемого в момент t, равна
![]()
Нетрудно видеть, что члены ряда (5) ― это те же члены ряда (1), но расположенные в обратном порядке. Отсюда следует, что общие суммы векселей и процентов остаются такими же, как и в случае «а», но изменяются распределения сумм и процентов по векселям.
В результате учета комплекта векселей в банке продавец получает сумму ![]() , которая в случае использования простой учетной ставки вычисляется так:
, которая в случае использования простой учетной ставки вычисляется так:
![]()
Величина есть приведенная стоимость всех векселей. Так как суммы векселей определялись двумя способами, то их приведенная стоимость также определяется по-разному.
Вариант «а».

Определим суммы в последнем равенстве:
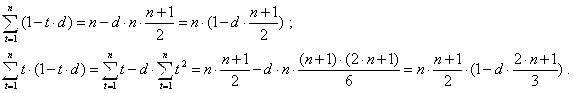
Подставляя полученные суммы в выражение (7), после ряда преобразований получаем:
![]()
Выражение в фигурных скобках обозначим через ![]() :
:
![]()
Если ![]() , то приведенная стоимость векселей равна стоимости товара, т. е. продавец полностью получает назначенную сумму. Если
, то приведенная стоимость векселей равна стоимости товара, т. е. продавец полностью получает назначенную сумму. Если ![]() , то он получит меньшую сумму. Для того, чтобы получить назначенную сумму, надо увеличить цену товара в
, то он получит меньшую сумму. Для того, чтобы получить назначенную сумму, надо увеличить цену товара в ![]() раз. Величину
раз. Величину ![]() называют корректирующим множителем. Этот же множитель используется для пересчета сумм векселей.
называют корректирующим множителем. Этот же множитель используется для пересчета сумм векселей.
Вариант «б». Приведенная стоимость всех векселей определяется по формуле:
![]()
Выполнив преобразования, аналогичные варианту «а», получаем:
![]()
Введем величину ![]() :
:
![]()
Величина ![]() служит корректирующим множителем для цены товара и сумм векселей.
служит корректирующим множителем для цены товара и сумм векселей.
Сравнивая выражения (9) и (11), нетрудно убедиться, что при ![]() (при
(при ![]() ), следовательно,
), следовательно, ![]() . Таким образом, вариант «б» требует большей корректировки цены.
. Таким образом, вариант «б» требует большей корректировки цены.
Анализ позиции покупателя [1, c. 313―314]
Покупатель оплачивает стоимость товара и проценты по кредиту последовательным погашением выданных им векселей. Совокупные издержки покупателя с учетом фактора времени определяются суммой потока платежей по векселям, приведенной на момент их выдачи. Номинальные стоимости векселей, как известно, рассчитываются двумя способами: вариант «а» ― проценты по кредиту начисляются на остаточную сумму основного долга, вариант «б» ― проценты начисляются на сумму погашения основного долга по векселю. Запишем формулы для приведенной суммы платежей по векселям с учетом того, что выполнена корректировка цены товара.
Вариант «а»:
![]()
Вариант «б»:
![]()
В этих формулах ― рыночная процентная ставка за период выплат по векселям. Эта ставка должна быть эквивалентна сложной годовой процентной ставке ![]() , характеризующей средний уровень ссудного процента на рынке. Уравнение эквивалентности имеет следующий вид:
, характеризующей средний уровень ссудного процента на рынке. Уравнение эквивалентности имеет следующий вид:
![]()
откуда
![]()
Покупатель заинтересован в минимизации издержек ![]() . Величина зависит от цены товара и параметров форфейтной операции
. Величина зависит от цены товара и параметров форфейтной операции ![]() :
:
![]()
Сложность этой функции затрудняет ее анализ, поэтому обычно выполняется серия расчетов с разными допустимыми значениями параметров и из них выбирается наилучший, дающий меньшее значение ![]() .
.
Анализ позиции банка [1, c. 316―317]
Банк, участвующий в форфейтной операции, получает доход в виде дисконта при учете векселей. Доход этот зависит от применяемой учетной ставки ![]() . Доходность долгосрочной финансовой операции принято оценивать эффективной ставкой сложных процентов. Эту ставку находят следующим образом. Пусть банк выплатил продавцу при учете векселей сумму
. Доходность долгосрочной финансовой операции принято оценивать эффективной ставкой сложных процентов. Эту ставку находят следующим образом. Пусть банк выплатил продавцу при учете векселей сумму ![]() , равную стоимости товара. Тогда при условии, что сумма и суммы векселей сбалансированы, имеет место равенство:
, равную стоимости товара. Тогда при условии, что сумма и суммы векселей сбалансированы, имеет место равенство:
![]()
где: ![]() ― дисконтный множитель по неизвестной процентной ставке
― дисконтный множитель по неизвестной процентной ставке ![]() , эквивалентной учетной ставке
, эквивалентной учетной ставке ![]() .
.
Равенство (14) представляет собой алгебраическое уравнение степени относительно переменной ![]() . Оно решается каким-либо из известных численных методов. По найденному значению вычисляется значение процентной ставки
. Оно решается каким-либо из известных численных методов. По найденному значению вычисляется значение процентной ставки ![]() :
:
![]()
От ставки за период выплат по векселям переходим к годовой эффективной ставке сложных процентов:
![]()
Ставка должна быть не ниже некоторого минимального допустимого для банка значения.
Для анализа форфейтной операции мною было разработано ПО в среде Delphi.
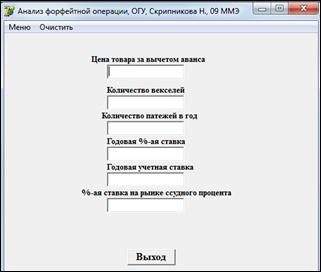
Рисунок 1. Интерфейс программы
Проанализируем форфейтную операцию с помощью разработанной программы со следующими параметрами:
![]() тыс. руб. (стоимость товара за вычетом аванса);
тыс. руб. (стоимость товара за вычетом аванса);
![]() (количество векселей);
(количество векселей);
![]() (количество платежей в год);
(количество платежей в год);
![]() % (годовая %-ая ставка);
% (годовая %-ая ставка);
![]() %; (годовая учетная ставка);
%; (годовая учетная ставка);
![]() % (%-ая ставка на рынке ссудного процента).
% (%-ая ставка на рынке ссудного процента).
Результат анализа форфейтной операции представлен на рисунках 2―5.
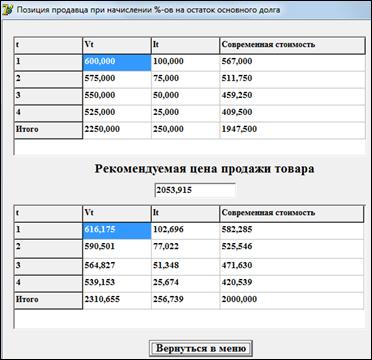
Рисунок 2. Анализ позиции продавца при начислении %-ов на остаток основного долга (вариант «а»)
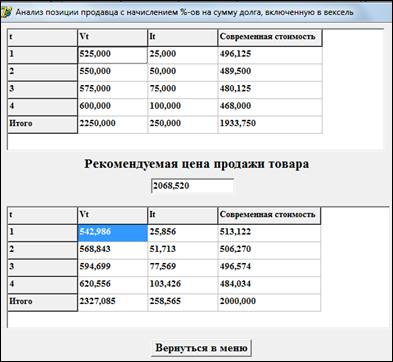
Рисунок 3. Анализ позиции продавца с начислением %-ов на сумму долга, включенную в вексель (вариант «б»)
Рисунок 4. Анализ позиции покупателя
Рисунок 5. Анализ позиции банка
Список литературы:
1.Четыркин Е.М. Финансовая математика: Учеб. ― М.: Дело, 2000, с. 305―318.
дипломов


Оставить комментарий