Статья опубликована в рамках: IV Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 20 сентября 2012 г.)
Наука: Технические науки
Секция: Моделирование
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
отправлен участнику
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ВЗАИМОСВЯЗИ ТОКОПРОВОДЯЩИХ ЭЛЕМЕНТОВ И КОНТАКТНОГО НАЖАТИЯ
Маркин Денис Игоревич
студент 4 курса, ФИОТ, ПГТА, г. Пенза
Е-mail: markinbel@bk.ru
Мешкова Оксана Александровна
студентка 5 курса, ФИОТ, ПГТА, г. Пенза
Е-mail: po4ta1994@mail.ru
Ермолаев Николай Александрович
научный руководитель, канд. тех. наук, доцент. каф. «Информационные технологии и системы» ПГТА, г. Пенза
Карпухин Эдуард Владимирович
научный руководитель, доцент каф. «Электроника и электротехника» ПГТА, г. Пенза
Тепловой режим работы высокочастотных вакуумных выключателей, переключателей и реле (высокочастотные вакуумные приборы коммутации — ВВПК) при пропускании тока высокой частоты зависит от омического сопротивления цепи их замкнутых контактов на высокой частоте, которое определяется геометрическими размерами токопроводников и контактным нажатием. Поэтому обеспечение нормального теплового режима ВВПК, являющегося гарантией надежной и долговечной их работы при эксплуатации, требовало установления взаимосвязи допустимого тока высокой частоты с геометрическими размерами их токопроводников и контактным нажатием. Для этого необходимо знать температуру в зоне контактирования, на поверхности токопроводящих элементов внутренней арматуры и внешней поверхности выводов (оболочки) при установившемся тепловом режиме. Знание температуры в зоне контактирования позволяет установить достаточность контактного нажатия и определить возможность изменения при этом фазового состояния материала контактов. С последним связано повышение вероятности диффузионного сваривания контактов в вакууме, их саморазмыкание при «взрыве» контактного мостика, интенсификация процессов газо- и паровыделения из контактов и токопроводников. В свою очередь, температура элементов вакуумплотной оболочки определяет термостойкость вакуумплотных швов, ускоряет диффузию газов внутрь вакуумплотной оболочки и старение материалов ее элементов.
Расположение контактов в высоком вакууме и специфика прохождения по ним тока высокой частоты не позволяют измерять температуру непосредственно в контактной зоне и на поверхности их токопроводников. Представление о температуре этих элементов могут дать только аналитические соотношения. Они известны для тепловых расчетов замкнутых контактов на постоянном и переменном токе промышленной частоты [1; 4; 7—11; 17—19]. Однако, эти соотношения не учитывают специфику прохождения тока высокой частоты и условия охлаждения контактной зоны и токопроводников в вакууме, а поэтому не могут использоваться для тепловых расчетов ВВПК. В связи с изложенным, возникла проблема получения аналитических соотношений для теплового расчета контактов ВВПК, которая решалась в настоящей работе.
Математическое моделирование взаимосвязи допустимого тока высокой частоты с геометрическими размерами токопроводников ВВПК и контактным нажатием проведено для контактной пары полусфера-плоскость, в котором заданы установившаяся температура высокочастотного токопроводника Ту.пр, его периметр П, длина L, удельное электрическое сопротивление ρ, теплопроводность λ, коэффициент теплоотдачи Ко [1], магнитная проницаемость μ и температурный коэффициент электрического сопротивления α. Заданы также температура окружающей среды То, пропускаемый ток высокой частоты If, его частота f.
Для рассматриваемой пары применима одномерная сферическая модель, для которой должно выполняться равенство 2ао= πb (b — радиус замещающей сферы [8]). Математической основой модели служат краевые задачи сопряжения [9]. Для нахождения температур нагрева элементов контактной зоны в вакууме составим уравнения теплового баланса [10] и объединим их условиями сопряжения [9]:
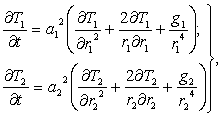 (1)
(1)
где: t — время > 0;
а12=λ1/с1m1 и а22=λ2/с2m2 — коэффициенты температуропроводности;
λ1 и λ2, m1 и m2, c1 и с2 — коэффициенты теплопроводности, удельной массы и удельной теплоемкости материалов контактной группы;
g1=If12ρ1/4π2λ2 и g2=If22ρ2/4π2λ2 — коэффициенты, характеризующие удельную мощность локальных источников тепла.
Для рассматриваемой системы уравнений в вакууме справедливы начальные и граничные условия идеального теплового контакта [7]:
![]() и
и ![]() . (2)
. (2)
В совокупности (1 и 2) приводятся к следующим уравнениям:
![]() и
и 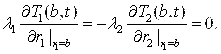 (3)
(3)
Решение (3) найдено с помощью интегрального преобразования Лапласа [2, 3, 5, 6, 12—16] в следующем виде:
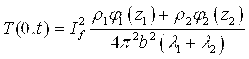 , (4)
, (4)
где: 
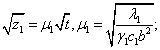
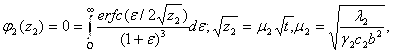
где: ![]() .
.
Из (4) при ![]() (установившийся тепловой режим), получено следующее соотношение для расчета установившейся температуры контактной зоны Ту.кз. при пропускании тока высокой частоты:
(установившийся тепловой режим), получено следующее соотношение для расчета установившейся температуры контактной зоны Ту.кз. при пропускании тока высокой частоты:
 . (5)
. (5)
Поскольку температура окружающей среды То может отличаться от нуля, а нагрев контактной зоны дополнительно происходит за счет выделяемого тепла в токопроводниках Ту.пр, то общая (максимальная) температура контактной зоны Тм.кз. определяется выражением:
![]() . (6)
. (6)
При этом изотерма максимальной температуры в контактной зоне, при прохождении через нее тока высокой частоты, будет расположена по окружности радиусом а0, ибо плотность тока высокой частоты и потери максимальны на поверхности цилиндра, эквивалентного контактному переходу с радиусом а0.
Зависимость температуры нагрева в любой точке токопроводников от выделяемой в зоне контактирования мощности потерь может быть рассчитана по следующему известному выражению [7, 9, 10, 18]:
 (7)
(7)
где х — текущая координата по направлению вдоль токопроводника или параллельно зоне контактирования.
В случае, когда температура окружающей среды не равна нулю, выражение (7) принимает вид:
 . (8)
. (8)
При одновременном учете температуры нагрева токопроводников пропускаемым через них током высокой частоты выражение (7) преобразуется к виду:
 (9)
(9)
Для нахождения максимальной температуры в контактной зоне необходимо знать температуру нагрева токопроводников от величины пропускаемого через них тока высокой частоты. Специфика его прохождения указывает на целесообразность применения в ВВПК тонкостенных токопроводников. Для них допустимо выравнивание температуры по периметру и сечению и связанное с этим усреднение величин внутренних источников тепла (g) и коэффициента теплопередачи (К). Поэтому нагрев таких токопроводников током высокой частоты может быть сведен к решению двумерной задачи теплопередачи для установившегося теплового процесса [7, 10, 17, 18].
Выделяемое при пропускании тока высокой частоты тепло dQ1 в единице длины токопроводника dx за время dt определяется выражением:
![]()
![]() (10)
(10)
где: If — A (действ. знач.),
Rf — Ом.
На повышение температуры токопроводника на dT расходуется тепло, определяемое известным соотношением [17]:
![]()
![]() (11)
(11)
где: с — удельнаятеплоемкостьединицывесаматериалатокопроводника, Вт •с/град.;
Sп — поперечное его сечение, см2;
m — удельный вес материала токопроводника, г/см3.
В вакууме отсутствует теплоотдача за счет конвекции, поэтому отвод тепла идет за счет излучения (Киз) с боковой поверхности Sб (см2) и теплопроводности (Кт) вдоль токопроводника:
![]()
![]() (12)
(12)
где: Т и То — температура токопроводника и окружающей среды,
С; Ко=Киз+Кт — общий коэффициент теплоотдачи, равный для круглого токопроводника (8—13)·10-4 Вт/см2 ·°С и для прямоугольного — (6—9)·10 - 4 Вт/см2 ·°С [16].
С учетом (10—12), уравнение теплового баланса запишется в виде:
![]() (13)
(13)
которое после преобразования и разделения по переменным преобразуется к следующему виду:
 (14)
(14)
а с учетом температурной зависимости сопротивления токопроводника,
уравнение (14) принимает вид:
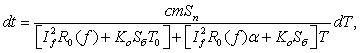 (15)
(15)
где: Ro(f) — активное сопротивление токопроводника на высокой частоте при температуре 0 ºС.
После интегрирования (15) по переменной t от нуля до t, по переменной Т от Тн (температура наружной поверхности вывода) до Т, получаем:
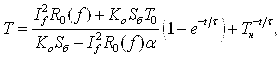 (16)
(16)
где: τ=сmSп/KoSб-If12R0(f)α — постоянная времени нагрева токопроводника до установившейся температуры в секундах. При t, стремящемся к бесконечности, Т=Ту.пр, т. е. равна установившейся температуре токопроводника, а поэтому из (16) имеем:
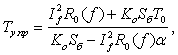 (17)
(17)
где: ![]() — температурный коэффициент сопротивления.
— температурный коэффициент сопротивления.
В начальный момент пропускания тока высокой частоты температура наружной поверхности вывода равна температуре окружающей среды, т. е. Тн=То. Учитывая это, после подстановки (17) в (16) имеем:
![]() (18)
(18)
Выражение (18) позволяет найти температуру токопроводника, с неизменным по длине сечением, в любой момент времени пропускания тока высокой частоты.
Поскольку в ВВПК токопроводники имеют переменное сечение, необходимо их температуру рассчитывать с учетом повышенного нагрева локального участка с меньшим сечением. Для определения изменения температуры нагрева токопроводника по длине в этом случае составим тепловой баланс для его элемента длиной dx с сечением Sп, отстоящего от участка с меньшим сечением на расстоянии х. Температура нагрева сечений, ограничивающих участок dx, соответственно равна: ![]()
Тогда количество тепла, входящего в элемент dx за время dt, равно:
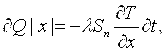 (19)
(19)
а выходящего из него за время dt:
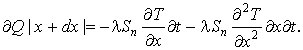 (20)
(20)
Оставшееся при этом в элементе dx за время dt количество тепла будет равно:
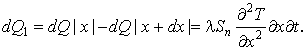 (21)
(21)
Оно суммируется с теплом dQ2, выделенным в элементе dx при прохождении по токопроводнику тока высокой частоты:
![]() (22)
(22)
Полученное элементом dx тепло частично идет на его нагрев:
![]() (23)
(23)
а частично отдается им в окружающую среду:
![]() (24)
(24)
в результате тепловой баланс элемента dx имеет вид:
![]() . (25)
. (25)
После подстановки вместо dQ их выражений, проведения преобразований и учета зависимости сопротивления от температуры получим следующее дифференциальное уравнение второго порядка для температуры перегрева V суженного участка токопроводника:
 (26)
(26)
Оно описывает изменение температуры как по длине токопроводника х, так и по времени пропускания t тока высокой частоты. Для ВВПК решение уравнения найдем для частного случая, когда требуется определить установившуюся температуру на расстоянии х от суженного участка. При этом максимальную температуру его примем одинаковой по всей длине. При установившемся режиме ![]() , а поэтому уравнение (26) принимает вид:
, а поэтому уравнение (26) принимает вид:
 (27)
(27)
Частное решение уравнения (27) при ![]() позволяет определить установившуюся температуру перегрева Vy.np однородного токопроводника при отсутствии суженного участка:
позволяет определить установившуюся температуру перегрева Vy.np однородного токопроводника при отсутствии суженного участка:
 (28)
(28)
С учетом (28), общее решение уравнения (27) имеет вид [6]:
![]() (29)
(29)
где Vc — температура перегрева суженного участка, a![]() Из граничных условий при х=1 и х=0 находим, что C1= 0 и С2 =Vmах-Vy.np. После их подстановки выражение (29) принимает вид:
Из граничных условий при х=1 и х=0 находим, что C1= 0 и С2 =Vmах-Vy.np. После их подстановки выражение (29) принимает вид:
![]() (30)
(30)
По аналогии с выражением для максимальной температуры перегрева суженного участка Vmах при пропускании тока промышленной частоты [15] выражение для Vmах применительно к току высокой частоты, после преобразования, принимает вид:
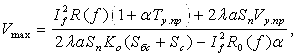 (31)
(31)
где: Sбс — площадь боковой поверхности,
Sc — поперечное сечение суженного участка.
Как правило, при разработке ВВПК задаются номинальные величины пропускаемого тока и напряжения на конкретной частоте рабочего диапазона, а также температура окружающей среды при номинальном токе. Допустимая температура элементов ВВПК зависит от применяемых материалов. Поэтому при расчете она выбирается по наименее теплостойкому материалу. При известности указанных характеристик, полученные выше в данном подразделе формулы для температуры нагрева и распределения ее вдоль токопроводника позволяют установить взаимосвязь тока высокой частоты с геометрическими размерами токопроводника, поэтому выражение (17) преобразуем к виду:
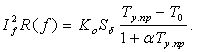 (32)
(32)
После подстановки Ro(f)=ρ0L/П![]() и Sб=ПL в (32) и решения полученного равенства относительно периметра токопроводника П, получим следующее выражение для его расчета по заданному току высокой частоты при длине токопроводника 1 см:
и Sб=ПL в (32) и решения полученного равенства относительно периметра токопроводника П, получим следующее выражение для его расчета по заданному току высокой частоты при длине токопроводника 1 см:
 (33)
(33)
В соответствии с (33) величина тока определяется периметром токопроводника П, допустимой его температурой Ту.пр, температурой окружающей среды То и коэффициентом теплоотдачи Ко. Рассчитанные по (33) зависимости периметра для токопроводников длиной 1 см из меди, серебра, молибдена и бронзы БрБ2, по заданному току частотой 30 МГц при Ту.пр = 125 °С и То = 100 °С, приведены на рис. 1.
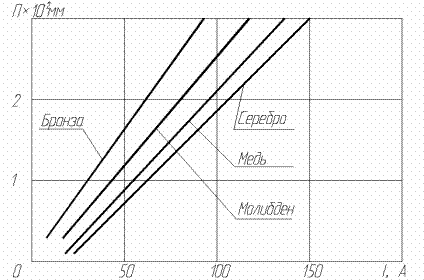
Рисунок 1. Зависимость периметра токопроводника длиной 1 см, от тока частотой
30 МГц в вакууме при температуре теплорассеивающего элемента 100 ˚С инормальном давлении воздуха вокруг ВВПК
Эти зависимости использованы для выбора диаметра D круглого, ширины h и толщины t плоского токопроводников созданных отечественных ВВПК. Указанные размеры могут быть рассчитаны и по следующим полученным в работе из (33) формулам:
 (34)
(34)
 (если задана t) (35)
(если задана t) (35)
 (если задана h). (36)
(если задана h). (36)
При задании отношения ширины к толщине n = h/t формулы для их расчета принимают вид:
 (37)
(37)
 (38)
(38)
где: ![]() — удельное электрическое сопротивление материала токопроводника при температуре 20 оС.
— удельное электрическое сопротивление материала токопроводника при температуре 20 оС.
При использовании в ВВПК токопроводников с переменным по длине сечением, под диаметром в формуле (34) понимается приведенный диаметр токопроводника Dnp=(Dmax+Dmin)/2, а под шириной в формулах (35 и 37) — приведенная ширина hnp=(hmax+hmin)/2 при неизменной толщине.
Взаимосвязь тока If с длиной находилась для токопроводника с эффективным рабочим сечением на высокой частоте 1 мм2. Для этого, по аналогии с изложенным выше, составлялся тепловой баланс для токопроводника неизменного сечения, с учетом выделения тепла не только при прохождении по нему тока высокой частоты, но и тепла, выделяемого на контактном переходе. После решения полученного дифференциального уравнения второго порядка [4, 6, 7, 9, 11, 19] для установившейся температуры токопроводника, логарифмирования и преобразования полученного выражения относительно тока, в данной работе получено следующее выражение:
 (39)
(39)
Из (39) следует, что на высоких частотах токопроводник должен иметь минимальную длину и выполняться из немагнитного металла с высокой рабочей температурой и высокими электро- и теплопроводностью. Рассчитанные по (39) зависимости длины токопроводников с эффективным рабочим сечением 1 мм2 по заданному току частотой 30 МГц для меди, серебра, молибдена и бронзы БрБ2 (рис. 2) использованы при разработке конструкций созданных отечественных ВВПК.
Для расчета активного сопротивления и индуктивности замкнутых контактов на высокой частоте также необходимо знать взаимосвязь тока с контактным нажатием при упругой Fк.у и пластической Fк.п деформации. С этой целью преобразуем известное выражение для допустимого тока через контактный переход Iко [8] относительно радиуса зоны контактирования ао:
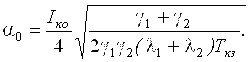 (40)
(40)
В случае упругой деформации одного из элементов контактной пары полусфера-плоскость (Rа = ![]() ), из (40) и формулы Герца [8] получим следующее выражение для расчета контактного нажатия (Fку) ВВПК:
), из (40) и формулы Герца [8] получим следующее выражение для расчета контактного нажатия (Fку) ВВПК:
 (41)
(41)
а для пластической деформацииFкп из (40) и формулы Герца [8] получим:
![]()
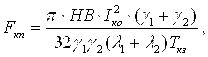 (42)
(42)
где: σ1 и σ2, E1 и Е2 — пределы прочности на смятие и модули упругости материалов контактов;
HB — твердость по Бринеллю у контакта из более мягкого металла.
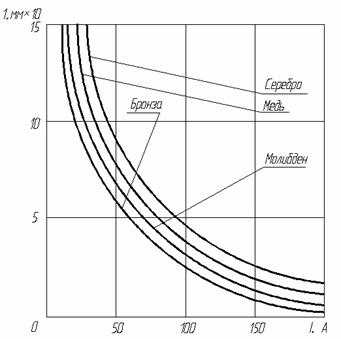
Рисунок 2. 3ависимость допустимой длины токопроводника с эффективным рабочим сечением 1 мм2 на частоте 30 МГц от тока в вакууме при температуре теплорассеивающего элемента 100 оС и нормальном давлении воздуха вокруг ВВПК
С учетом требования конструктивного запаса по току высокой частоты Кт в 1,2 раза, устойчивости к механическим нагрузкам Км в 1,5 раза, запаса по контактному нажатию из-за износа подвижных сочленяемых поверхностей при длительной коммутации Ки=1,05 и электродинамической силы расталкивания контактов Fэ [2], выражения для контактного нажатияполучены в данной работе в следующем виде:
· при упругой деформации:
 (43)
(43)
· при пластической деформации:
 (44)
(44)
· при пластической деформации обоих контактов:
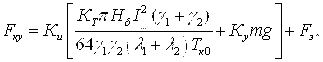 (45)
(45)
где: ![]() и
и ![]() — твердость по Бринеллю материалов контактов;
— твердость по Бринеллю материалов контактов;
g — ускорение силы тяжести;
m — масса подвижных элементов узла подвижного контакта и подвижных элементов электромагнита;
R — радиус сферы контакта.
Поскольку на частотах до граничной частоты fo в токопрохождении участвует все сечение а-пятна, то для расчета электродинамической силы расталкивания контактов при пропускании через них тока высокой частоты можно воспользоваться известным соотношением [2] в следующем преобразованном для диапазона высоких частот виде:
 (46)
(46)
Для контактной группы на переключение необходимо учитывать уменьшение контактного нажатия между замкнутыми контактами от электродинамической силы притяжения Fэп между вторым неподвижным и подвижным контактами. Для расположенных в вакууме (![]() =1) электродов она рассчитывается по следующему известному выражению [19]:
=1) электродов она рассчитывается по следующему известному выражению [19]:
![]() (47)
(47)
где: U — рабочее напряжение (ампл.знач.);
h — длина межконтактного зазора;
S — площадь поверхностей, между которыми возникает Fэп.
Из (43—45) следует, что для повышения пропускаемого тока высокой частоты необходимо повышать контактное нажатие. Применимость этих выражений для расчета контактного нажатия созданных ВВПК подтверждена многократными результатами их испытаний на пропускание заданного тока высокой частоты и воздействие механических нагрузок.
ЗАКЛЮЧЕНИЕ
Полученные аналитические соотношения позволяют на этапе проектирования ВВПК по заданному току высокой частоты и рабочему напряжению рассчитать требуемые размеры токопроводящих элементов и контактного нажатия и оценить термический режим работы контактной группы ВВПК при пропускании заданного тока высокой частоты. Применимость соотношений подтверждена многократными испытаниями созданных отечественных ВВПК на пропускание заданного тока высокой частоты и устойчивость к воздействию механических нагрузок, а также при длительной их эксплуатации в радиопередающей аппаратуре различного назначения.
Список литературы:
1.Арсенин В.Я. Методы математической физики. М.: Наука, 1984. — 383 с.
2.Бочкарев B.C. Особенности работы высокочастотных вакуумных выключателей и переключателей в высокочастотных цепях// Электронная техника. Сер.5. Радиодетали и радиокомпоненты. — 1985. — Вып. 4 (61). С. 39—42.
3.Брон О.Б. Электрические аппараты с водяным охлаждением. М.: Энергия, 1967. — 325 с.
4.Бугров Я.С., Никольский В.И. Высшая математика. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции одного переменного. М.: Наука, 1981. — 448 с.
5.Дульнев Г.Н., Тарновский Н.Н. Тепловые режимы электронной аппаратуры. Л.: Энергия, 1971. — 246 с.
6.Залесский А.М., Кукеков Г.А. Тепловые расчеты электрических аппаратов. М.: Энергия, 1967. — 379 с.
7.Зарубин B.C. Инженерные методы решения задач теплопроводности. М: Энергоатомиздат, 1983. — 328 с.
8.Исакова А.В. Определение температуры перегрева контактных пар из разных металлов/ Электрические контакты: Науч.-техн. сб. М.: Энергия, 1967.С. 92—96.
9.Камке Э. Справочник по обыкновенным дифференциальным уравнениям /Пер. с англ./. М.: Наука, 1979. — 536 с.
10.Ким Е.И., Омельченко В.Т., Харин С.Н. Математические модели тепловых процессов в электрических контактах. лма-Ата: Наука, 1977. — 236 с.
11.Корн Г., Корн Н. Справочник по математике / Пер. с англ./ М.: Наука, 1974. — 831 с.
12.Краус А.Д. Охлаждение электронного оборудования /Пер. с англ./. Л.: Энергия, 1971. — 247 с.
13.Кузовлев В.А. Техническая термодинамика и основы теплопередачи. М.: Высшая школа, 1975. — 303 с.
14.Кукеков Г.А. Проектирование выключателей переменного тока высокого напряжения. М.: Госэнергоиздат, 1961. — 256 с.
15.Новиков Ю.Н. Теория и расчет электрических аппаратов. Л.: Энергия, 1970. — 328 с.
16.Соболев С.Н. Расчет и конструирование низковольтной электрической аппаратуры. М.: Высшая школа, 1972. — 256 с.
17.Хольм Р. Электрические контакты/ Пер. с нем./. М.: ИЛ, 1961. — 464 с.
18.Цой П.П. Методы расчета задач тепломассопереноса. М.: Энергоатомиздат, 1984. — 416 с.
19.Шилов Г.Е. Математический анализ. Функции одного переменного. Ч. 1, 2. М.: Наука, 1969. — 546 с.
отправлен участнику



Оставить комментарий