Математическое моделирование угла наклона плоскости двухкоординатного магнитострикционного наклономера относительно горизонтальной плоскости

Маркин Денис Игоревич

студент 4 курса, ФИОТ, ПГТА, г. Пенза

Е-mail: markinbel@bk.ru

Володин Василий Анатольевич

студент 4 курса, ФИОТ, ПГТА, г. Пенза

Е-mail: Yahuu92@mail.ru

Ермолаев Николай Александрович

научный руководитель, канд. тех. наук, доцент. каф. «Информационные технологии и системы» ПГТА, г. Пенза

Воронцов Александр Анатольевич

научный руководитель, аспирант каф. «Электроника и электротехника» ПГТА, г. Пенза

Бурное развитие науки и техники невозможно без разработок, исследований и внедрения новых приборов и устройств, предназначенных для контроля и диагностики механизмов и сооружений во всех видах производственной деятельности. К таким приборам относятся наклономеры, предназначенные для определения углов наклона объекта. Наклономеры используются для определения положения различных высотных сооружений, плотин, для определения величины прогибов и деформаций различного рода опор и балок, контроля углов наклона автомобильных и железных дорог при их строительстве, ремонте и эксплуатации, определения угла наклона дорожных грейдеров, асфальто-укладчиков, подъемников, кранов и экскаваторов и т. д.

Для этих целей в последнее время все чаще находят применение магнитострикционные наклономеры. От известных наклономеров, таких как [1, с. 3—4] их отличает высокая точность, быстродействие, широкий диапазон преобразования, относительно невысокая себестоимость и простота реализации.

Магнитострикционные наклономеры можно условно разделить на две основные группы — однокоординатные (ОМН) и двухкоординатные (ДМН). ДМН позволяют проводить одновременное измерение двух углов наклона объекта во взаимноперпендикулярных плоскостях относительно вертикали или горизонтали.

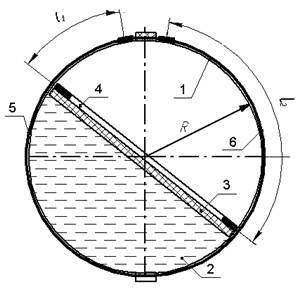
Рисунок 1. Первичный преобразователь двухкоординатного магнитострикционного наклономера.

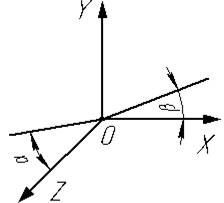
Рисунок 2. Углы наклона объекта относительно вертикальной плоскости

Один из вариантов реализации первичного преобразователя двухкоор-динатного магнитострикционного наклономера приведен на рисунке 1.

Он содержит магнитострикционный преобразователь перемещений, выполненный в виде сферического корпуса 1 из немагнитного материала, например пластика, с заполненной наполовину рабочей жидкостью 2, поплавковым элементом 3 с кольцевым постоянным магнитом 4, однотипными С-образными звукопроводами 5, 6 из магнитострикционного материала [2].

Одной из возможностей предложенной конструкции двухкоординатного магнитострикционного наклономера является возможность косвенного определения кодов величины и знака угла наклона объекта в отклоняемой плоскости  по рассчитанным значениям кодов углов отклонения объекта в двух взаимно перпендикулярных плоскостях относительно горизонтали ( и  соответственно), о чем не сказано в упомянутом источнике. Целью данной статья является вывод, проверка и моделирование формулы расчета угла  через  и .

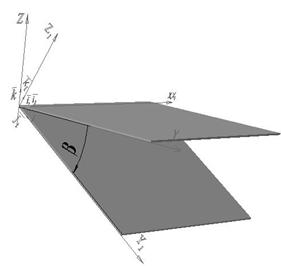
Для этого представим ДМН в виде горизонтальной плоскости П1 с базисными векторами , , (рисунок 3 а).

                                 а)                                                           б)

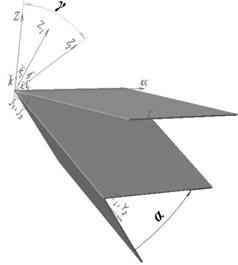
Рисунок 3. Поворот ДМН в одной и двух взаимноперпендикулярных плоскостях

Перейдем к новой системе координат К1 с репером <0,,,>, смещенной на произвольный угол  в плоскости YOZ относительно К. Базисные вектора систем координат К и К1 будут связаны между собой в соответствии с выражением 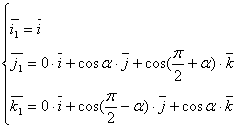(1):

                                          (1)

Поворачивая систему координат К1 на произвольный угол  (рисунок 3б) в плоскости XOZ, получаем систему координат К2 с репером <0,,,>. Базисные вектора систем координат К1 и К2 будут связаны между собой соответственно:

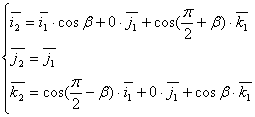                                     (2)

Cвязь между старым базисом () и новым () базисными векторами, согласно (1) и (2), определяется выражением (3), где коэффициент перед   и есть направляющий косинус угла  (4).

   (3)

                               (4)

Знак угла , а также четверть, в которой происходит отклонение поляризатора относительно вертикальной плоскости можно узнать по отклонениям  углов  и .

Для численной проверки формулы (4) авторами статьи была собрана экспериментальная установка, изображение которой приведено на рисунке 4, состоящей из пластины из оргстекла 1, имитирующей плоскость отклонения ДМН от горизонтальной поверхности, представленной поверхностью стола, трех транспортиров 2, предназначенных для фиксации углов отклонения во взаимноперпендикулярных плоскостях  и  относительно горизонтальной плоскости, а также угла наклона плоскости ДМН относительно последней . Так как угол наклона плоскости удобнее измерять над поверхностью пластины 1, то для задания горизонтальной плоскости, относительно которой и определялся угол наклона плоскости  был использован жидкостный однокоординатный уровень 3. Для определения  направления отклонения плоскости в конструкцию был использован жидкостный двухкоординатный уровень 4.

Так, для одного из опытов при изменении одного из углов отклонения  с помощью книг разной толщины 5 и при неизменном значении второго угла наклона  были получены результаты, приведенные на рисунке 5. Как видно, полученные экспериментальным путем значения отличаются не более 2˚ от рассчитанных по формуле (4), что свидетельствует о достоверности полученной формулы.

Рисунок 4 Экспериментальная установка

Рисунок 5. Зависимость угла наклона плоскости ДМН  от  при =30˚, полученная по расчетной формуле (а) и экспериментальным путем (б)

Данная погрешность вычислений вполне допустима для приведенного стенда, так как систематическая погрешность каждого из транспортиров составляет 0,5˚. Также нужно учитывать случайную погрешность, вызванную несовершенством органов чувств наблюдателя.

Таким образом, в данной статье была получена и экспериментально проверена расчетная формула по определению угла наклона  плоскости ДМН относительно горизонтальной плоскости. Это позволяет существенно увеличить область применения приборов данного класса.

Список литературы:

1. Виноградов С.А., Трофимов А.И.. Ультразвуковой наклономер. Патент РФ № 2084823 МПК: G01C9/22, G01C9/18. Бюл. № 3, 1997. — 12 с.

2. Воронцов А.А., Демин С.Б, Демин Е.С. Магнитострикционный двухкоординатный наклономер. Патент РФ № 2389975. МПК: G01C9/18. Бюл. № 14, 2010. — 10 с.

3. Гриднев Д.Г., Канониди Х.Д., Канониди К.Х.. Наклономер. Патент РФ № 2187829 МПК: G01V7/02. Бюл. № 3, 2002. — 10 с.

4. Таймазов Д.Г., Двухкоординатный струнный наклономер. Патент РФ № 2287777 МПК: G01C9/00. Бюл. № 5, 2004. — 11 с.