РЕШЕНИЕ ЗАДАЧИ РАСПРЕДЕЛЕНИЯ ДЕНЕЖНЫХ РЕСУРСОВ ПАРТИЙ ДЛЯ МИНИМИЗАЦИЯ ПОТЕРЬ ВО ВРЕМЯ ПРЕДВЫБОРНЫХ КОМПАНИЙ

Литвин Вероника Николаевна

студентка 4 курса, кафедра математических методов системного анализа, НТУУ «КПИ», г Киев

Е-mail: litvin_veronika@mail.ru

Шмыговская Ольга Леонидовна

студентка 4 курса, кафедра математических методов системного анализа, НТУУ «КПИ», г Киев

Е-mail: ol.shmyg@gmail.com

Подладчиков Владимир Николаевич

научный руководитель, доктор технических наук, проф., НТУУ «КПИ»

Введение

Нестабильность политических взглядов и изменчивость предпочтений – основные проблемы предвыборной гонки. В борьбе за электорат, партиям приходится прибегать к разному рода оценкам и прогнозам. Предвиденье становится основным оружием в борьбе за победу. Когда каждый голос может стать решающим, цена ошибки слишком велика. Учитывая условия жесткой конкуренции, не приходится рассчитывать на достоверные данные относительно конкурентов, и любые расчеты имеют только оценочный характер, но при этом уже могут показать главные тенденции. При переоценке собственного потенциала, партия может понести серьезные убытки, вкладывая деньги в деятельность в регионах, которая не принесет желаемого результата.

Оптимизационную модель для определения стратегии двух конкурирующих организаций в условиях наличия информации о действиях конкурентов было рассмотрено в работе [1]. В работе [2] предложено теоретико-игровую модель борьбы двух конкурирующих учреждений, для которой доказано существование решение задачи оптимизации, что максимизирует выигрыш при ограниченных денежных ресурсах. Обобщение решения задачи оптимизации стратегии для произвольного количества участников конкурентной борьбы рассматривается в работе [3], в которой с использованием численных методов получено решение оптимизационной задачи для 10 конкурирующих организаций.

Поэтому очень важно просчитать все возможные риски, рассматривая наихудшие варианты, чтобы найти предел, после которого нужно остановится. Грамотное распределение денежных ресурсов по регионам сможет увеличить преимущества партии и поможет избежать непредвиденных ситуаций.

Постановка задачи оптимизации

Рассмотрим задачу для трех конкурирующих партий А, В и С. Предусмотрено, что они действуют в n регионах, в каждом из которых количество избирателей равно . Цель каждой из трех конкурирующих партий – максимизировать количество своих избирателей, которые отдали им предпочтение. Обозначим через  – коэффициент влияния первой партии А в і-ом регионе, через -  - коэффициент влияния партии В, через   - коэффициент влияния партии С.

Для увеличения выигрыша партии выделяют капиталы ,  и  соответственно и распределяют по регионам там образом, что , , , де , ,  - части капитала, что вкладываются в -й регион первой, второй и третьей партией.

В роботе [3] введено функции выигрыша, которые отображают зависимость процента количества населения, что отдало предпочтение j-й партии в i-ом регионе, от вложенного капитала и влияния в этом регионе. Используем их.

Функция выигрыша для партии А - ,  для партии В - , для партии С - . Функция показывает, какую часть населения партия может привлечь на свою сторону в -ом регионе.

Предусмотрено, что все партии одновременно конкурируют за сторонников в каждом регионе. Количество населения, что отдало предпочтение конкретной партии в -ом регионе, определяется соотношением:  - для партии А, ,  - для партии В,  - для партии С.

Тогда общий выигрыш первой партии - , для второй партии - , для третьей партии - .

Задача максимизации выигрыша для каждой партии состоит в выборе таких значений капитала, что максимизируют функция качества.

Задача нелинейного программирования формулируется следующим образом.

Для первой партии А:

Для второй партии В:

Для третьей партии С:

Условия , ,  взяты из соображений, что суммарные расходы по регионам, не могут превысить общий капитал.

Решения может быть найдены с использованием квазиньютоновского метода [4].

Функция Лагранжа для первой партии А -  для второй партии В - 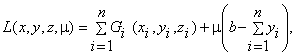 для третьей партии С - 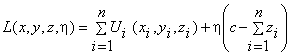, где  - множители Лагранжа.

Получим необходимые и достаточные условия решения задачи максимизации выигрыша для партии А при произвольном наборе , :

Аналогично для партии В при произвольном наборе , :

Так же для партии С при произвольном наборе , :

Решение задачи одновременной максимизации выигрыша партиями может быть получено как общее решение объединенной системы (3n+3) нелинейных уравнений с (3n+n) неизвестными.

Существование решения задачи оптимизации

Поскольку партии пытаются одновременно максимизировать свой выигрыш, то решение задачи одновременной максимизации выигрыша между всеми партиями может быть получен как решение объединенной системы.

Или

                                                             (1)

Решение этой системы (3n+3) нелинейных уравнений с (3n+n) неизвестными существует, ясли определитель матрицы Якоби этой системы не равен нулю.

Матрица Якоби размерности (3n+3)´(3n+3) для системы (1) имеет вид:

Для доказательства существования решения системы (1) покажем невырожденность матрицы Якоби .

Представим матрицу  в блочном виде

,

Где , ,  , , , ,

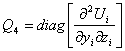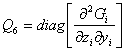
Функции ,  та  имеют непрерывные вторые производные. В виду адитивности, матрицы Гессе для них имеют диагональную форму:

, ,

,

, , .

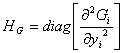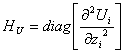
Покажем, что матрица  невырожденная. Сведем ее к диагональному виду.

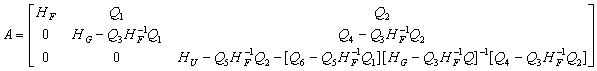
Тогда

Матрицы  та  имеют диагональную форму.

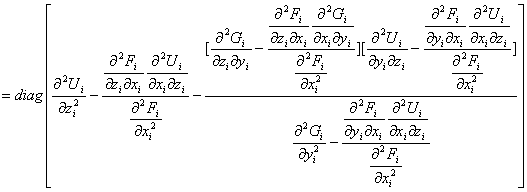
считая, что , , ,

, ,

, ,

,

Получим, что диагональный элемент матрицы А имеет вид

Соответственно, каждый множитель в правой части выражения  отличен от нуля и матрица  невырожденная.

Рассмотри матрицу .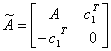

Применив прием аналогичный предыдущему, получим

.

Поскольку матрица невырожденная, то .

Представим Якобиан в виде

.

Тогда

Следовательно, решение задачи максимизации существует.

Выводы

Нами был предложен один из возможных вариантов распределения денежных средств по регионам, которым партия может воспользоваться во время предвыборной кампании для  оценки своего потенциала. Своевременная реакция и соответственные изменения в деятельности (дополнительное финансирование, коррекция агитационной программы, направление ресурсов на определенные регионы) поможет достичь желаемого результата и существенно сократить убытки. Данные, полученные в результате работы модели, показывают результат, что соответствует тенденции с допустимой погрешностью.

Список литературы:

1. Н. І. Недашківська, В. В. Остапенко, О. С. Остапенко. Теоретико-ігрова модель боротьби партій за електорат // Системні дослідження та інформаційні технології.-2003.-№ 4.- С. 113‑119.
2. Остапенко В. В, Остапенко О. С, Подладчикова Т. В. Оптимизация стратегии политических партий в ходе предвыборной кампании // Системный анализ и информационные технологии. – 2006. -№ 2. – С. 84‑98.
3. Подладчикова Т. В., Подладчіков В. М., Романенко В. Д. Координуюче управління розподілом обмежених ресурсів для максимізації виграшу конкуруючих організацій // Нові технології. – 2011. -№ 3(33). ‑ С.55‑61.
4. Реклейтис Г., Рейвиндран А., Рэгсдел К. Оптимизация в технике: В 2-х кН. Кн.1. Пер. с англ. - М.: Мир, 1986. – С. 196‑224.