Статья опубликована в рамках: I Международной научно-практической конференции «Научное сообщество студентов: МЕЖДИСЦИПЛИНАРНЫЕ ИССЛЕДОВАНИЯ» (Россия, г. Новосибирск, 06 декабря 2011 г.)
Наука: Технические науки
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ПРИМЕНЕНИЕ ТЕОРИИ КЛЕТОЧНЫХ АВТОМАТОВ ПРИ МОДЕЛИРОВАНИИ ПРОЦЕССОВ РАЗМЕЩЕНИЯ ОБЪЕКТОВ РОЗНИЧНОЙ ТОРГОВЛИ НА ТЕРРИТОРИИ ГОРОДА
Развитие территории города с населением порядка миллиона человек, покрывающей площадь земли в несколько сотен квадратных километров, является достаточно сложным для точного описания процессом. Проблема прогнозирования такого рода процессов требует разработки принципиально новых способов формализации соответствующих явлений в рамках имеющихся математических методов. Пространственный характер взаимодействия отдельных структурных элементов территории, идентифицирующихся некоторым промежуточным внутренним состоянием, дает аналогию с известными алгоритмическими задачами в области применения клеточных автоматов.
Обычно под клеточным автоматом подразумевается дискретная динамическая система, поведение которой полностью определяется в терминах локальных зависимостей [5]. Ключевым в решении поставленной задачи является применение подхода, широко зарекомендовавшего себя в сфере естественных и информационно-вычислительных наук. Суть его заключается в представлении наблюдаемой системы в виде однородной структуры, эволюция которой происходит путем пошагового воспроизведения [1]. На основе исследовании конкретной предметной области обнаруживаются важнейшие параметры, определяющие состояние элемента системы на каждом шаге. С развитием компьютерных мощностей, позволяющих производить крупные вычислительные эксперименты, подобные дискретные модели обретают все большую актуальность при изучении динамики любого рода систем, представимых в виде некоторой пространственной структуры.
Теория клеточных автоматов имеет широкое практическое применение во многих областях научных исследований, в сфере моделирования различных физических и информационных процессов [2,3,4]. В том числе с ее помощью описываются такие явления, как образование микроструктуры материала, диффузия вещества, теплопроводность, химические реакции, преобразование и шифрование информации, создание иерархической организации, урбанизация, работа дорожного перекрестка, макродинамика экопопуляций, движение толпы, работа и восстановление ритма сердца.
В качестве двумерного клеточного автомата рассматривается двумерная система (пространство), являющаяся однородной сеткой из клеток (ячеек). Каждая клетка однозначно характеризуется парой координат , где , . Число клеток (размер пространства) конечно, поэтому на границах системы стоит дополнительно определить краевые условия. О граничных условиях речь пойдет ниже.
Пусть время t дискретно и имеет единичный шаг , т.е. , где .
Для описания эволюции любой отдельно взятой ячейки используются два вектора состояния: вектор динамических переменных , определяющий состояние ячейки, и вектор управляющих параметров , где соответственно K — общее число динамических переменных, L — общее число управляющих параметров. Динамические переменные xk количественно идентифицируют моделируемые объекты, распределенные по клеткам сетки. Управляющие параметры yl указывают на факторы, существенно влияющие на динамику моделируемых объектов, при этом их собственный характер изменения не имеет принципиального значения для конкретной задачи. Предполагается, что , и не зависит от времени t.
Для вычисления нового состояния ячейки сетки на каждом дискретном шаге необходимо определить правило перехода , . Правила носят локальный (т.е. будущее внутренне состояние клетки зависит только от выбранного некоторым образом ближайшего окружения) и стационарный характер. Следовательно, , где , , пробегают значения, соответствующие некоторому окружению ячейки .
Компоненты векторов нового состояния клетки формируются как точечные отображения следующим образом:
Для упрощения задачи исследования в качестве моделируемых объектов xk рассматриваются точки розничной торговли полностью или частично продовольственного типа. Поэтому вводится количество динамических переменных . Каждая динамическая переменная xk количественно (в единицах) определяет наличие соответствующих объектов:
x1 — продуктовые гипермаркеты;
x2 — продуктовые супермаркеты;
x3 — продуктовые магазины;
x4 — продуктовые рынки.
Адекватный выбор компонент вектора управляющих параметров является трудоемкой задачей. Очевидно, что процесс развития инфраструктуры города, в частности, насыщение территории торговыми точками, носит многофакторный характер. На данном этапе исследования, в расчет берутся показатели, влияние которых должно быть экспериментально проверено на основании существующих электронных баз данных. В представляемой модели рассматриваются управляющих параметров. Однако не исключена потребность в увеличении или уменьшении их числа при последующей доработке модели.
Итак, выделяются следующие управляющие параметры (в скобках указана размерность или возможные принимаемые значения): y1 — благоприятность ландшафта местности (если более 50% клетки занято водохранилищами, лесными массивами и прочими препятствиями к строительству природного характера, принимает значение 0, иначе – принимает значение 1), y2 — площадь частного сектора (в % от площади клетки); y3 — суммарная длина автомобильных дорог и шоссе (в м); y4 — количество транспортных узлов (в единицах), к которым относятся станции метро, пригородных электропоездов, остановки городского общественного транспорта; y5 — количество жилых частных домов (в единицах); y6 — количество жилых многоэтажных домов (в количестве этажей, умноженном на количество подъездов); y7 — количество административных зданий (в количестве этажей), при этом, в случае расположения административных помещений в жилых многоэтажных домах, считается, что первый этаж полностью административного типа, остальные — полностью жилого типа; y8 — количество строящихся жилых многоэтажных домов (в количестве этажей, умноженном на число подъездов); y9 — количество строящихся административных зданий (в количестве этажей этажи); y10 — площадь промышленной зоны (в % от площади клетки); y11 — количество объектов массового скопления людей, занимающих площадь порядка более чем 2000 м2 (в единицах), к которым относятся крупные торговые центры, культурно-развлекательные учреждения, парки отдыха, вокзалы, больницы, студенческие городки высших учебных заведений; y12 — количество объектов массового скопления людей, занимающих площадь менее чем 2000 м2 (в единицах), к которым относятся школы, детские сады, поликлиники.
После полного определения необходимых компонентов векторов состояния  и
и  , возможен переход к описанию механизма эволюции клеточной структуры. Работа клеточных автоматов носит синхронный характер — обновление внутриклеточных состояний производится в дискретный момент времени ti строго для всего набора клеток одновременно.
, возможен переход к описанию механизма эволюции клеточной структуры. Работа клеточных автоматов носит синхронный характер — обновление внутриклеточных состояний производится в дискретный момент времени ti строго для всего набора клеток одновременно.
В качестве важнейшего пункта изучения работы клеточного автомата с необходимостью рассматривается характер влияния «клеток-соседей», лежащий в основе функционирования любого рода клеточного автомата. На знании этой информации формируются 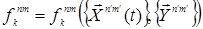 — правила обновления клетки на каждом шаге развития автомата. Для каждой клетки с координатами
— правила обновления клетки на каждом шаге развития автомата. Для каждой клетки с координатами  в качестве «соседей» по ее периметру обозначаются восемь клеток с координатами
в качестве «соседей» по ее периметру обозначаются восемь клеток с координатами 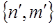 , где
, где 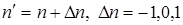 и
и  . Для каждой динамической переменной xk существует строго определенное для нее правило обновления
. Для каждой динамической переменной xk существует строго определенное для нее правило обновления 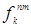 , причем в нем заложен механизм суммарного влияния соседних ячеек. Поэтому, для указания граничных условий используется следующий прием: территория за пределами клеточной сетки представляется в виде воображаемых клеток с полностью нулевыми по всем компонентам векторами состояний. Это предположение является естественным, поскольку изначально пространственная конфигурация клеток размечается на карте исходя из условия отсутствия за ее границами по периметру важной для исследования, принадлежащей городу территории.
, причем в нем заложен механизм суммарного влияния соседних ячеек. Поэтому, для указания граничных условий используется следующий прием: территория за пределами клеточной сетки представляется в виде воображаемых клеток с полностью нулевыми по всем компонентам векторами состояний. Это предположение является естественным, поскольку изначально пространственная конфигурация клеток размечается на карте исходя из условия отсутствия за ее границами по периметру важной для исследования, принадлежащей городу территории.
Динамика развития торговых точек xk при учете управляющих параметров yl будет воспроизводиться согласно следующему уравнению:
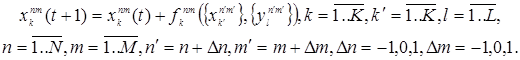
В качестве упрощения, принимается утверждение о том, что состояние клетки на новом шаге определяется лишь в зависимости от значений динамических переменных у окружающих ячеек-»соседей» и набора управляющих параметров внутри клетки:
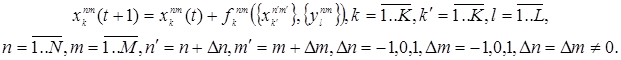
Для дальнейшего исследования допускается приближение, предполагающее линейность правил обновлений как функций от переменных в модели:
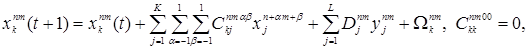 (1)
(1)
где 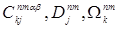 – постоянные коэффициенты.
– постоянные коэффициенты.
Пусть правая часть равенства (1) обозначается как . Далее задача сводится к нахождению коэффициентов
. Далее задача сводится к нахождению коэффициентов 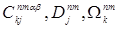 с помощью метода наименьших квадратов, таким образом, чтобы сумма квадратов отклонений эмпирических значений
с помощью метода наименьших квадратов, таким образом, чтобы сумма квадратов отклонений эмпирических значений 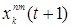 от расчетных
от расчетных  была минимальной:
была минимальной:

где T – число временных срезов.
К сожалению, данный метод в реальности не применим, поскольку значение T должно превышать число оцениваемых коэффициентов. Исходя из этого, для решения проблемы с необходимостью предпринимаются следующие шаги. Во-первых, предполагается однородность коэффициентов 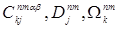 по всей клеточной сетке, что позволяет перейти к оперированию с коэффициентами
по всей клеточной сетке, что позволяет перейти к оперированию с коэффициентами 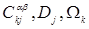 , количество которых существенно меньше. Во-вторых, при подробном рассмотрении восьмиклеточного окружения каждой ячейки на двумерной сетке, можно сделать вывод о том, что крайние угловые «соседи», оказывают равноценное влияние на коэффициенты
, количество которых существенно меньше. Во-вторых, при подробном рассмотрении восьмиклеточного окружения каждой ячейки на двумерной сетке, можно сделать вывод о том, что крайние угловые «соседи», оказывают равноценное влияние на коэффициенты 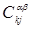 , для которых выполняется условие —
, для которых выполняется условие — 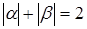 . Аналогично, предполагается равнозначность влияния боковых клеток-»соседей», воздействующих на коэффициенты
. Аналогично, предполагается равнозначность влияния боковых клеток-»соседей», воздействующих на коэффициенты 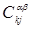 , для которых выполняется условие —
, для которых выполняется условие — 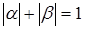 .
.
Знание коэффициентов  и
и 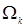 дает возможность полного описания клеточного автомата и, соответственно, позволяет моделировать эволюцию клеточного автомата, отображающего в любой будущий момент времени
дает возможность полного описания клеточного автомата и, соответственно, позволяет моделировать эволюцию клеточного автомата, отображающего в любой будущий момент времени  территориальное размещение торговых точек.
территориальное размещение торговых точек.
Список литературы:
- Аладьев В.З. Классические однородные структуры. Клеточные автоматы. Таллинн: Fultus Publishing. 2009.
- Беркович С.Я. Клеточные автоматы как модель реальности: поиски новых представлений физических и информационных процессов. М.: Изд-во МГУ. 1993.
- Ванаг В.К. Исследование пространственно распределенных динамических систем методами вероятностного клеточного автомата.// Науч.-техн. журн: Успехи физических наук. Т.69.№5. 1999.
- Лобанов А.И. Модели клеточных автоматов.// Науч.-техн. журн. Компьютерные исследования и моделирование. Т.2. № 3. С. 273‑293. 2010.
- Тоффоли Т., Марголус Н. Машины клеточных автоматов. М.: Мир. 1991.
дипломов


Оставить комментарий