Статья опубликована в рамках: I Международной научно-практической конференции «Научное сообщество студентов: МЕЖДИСЦИПЛИНАРНЫЕ ИССЛЕДОВАНИЯ» (Россия, г. Новосибирск, 06 декабря 2011 г.)
Наука: Технические науки
Секция: Моделирование
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ОХЛАЖДЕНИЕ КАПЕЛЬ ЖИДКОСТИ В ВОЗДУШНОМ ПОТОКЕ
Предложена структура физической модели для тепло-массобменного процесса в оросителях градирен. В математической модели предлагается дискретные потоки заменять эквивалентными по эффекту охлаждения потоками, в которых перемещение капель и течение пленки жидкости осуществляется непрерывно. Получены дифференциальное и расчетное уравнения по определению температуры охлаждения жидкости для капельного потока.
В настоящие время на химических, нефтехимических и энергетических предприятиях широко используется водяное охлаждение, которое осуществляется с помощью градирен различных конструкций. Отсутствие надежных методов расчета тепло-массобменного процесса в оросителях градирен вынуждает использовать при их проектировании расчетные формулы и рекомендации, полученные опытным путем [2]. Влияние на тепломассообмен в оросителе множества факторов и взаимозависимость некоторых из них затрудняют, а в отдельных случаях и просто не позволяют анализировать работу градирен при изменении условий ее работы. Всесторонний анализ работы градирен возможен только при наличии математической модели процесса тепломассообмена протекающего в оросителе, однако в настоящее время таких моделей для наиболее распространенного капельно-пленочного течения потока воды сквозь насадку не имеется, а в известных моделях рассматриваются модели только для чисто капельных или пленочных потоков [2]. Для появившихся в последние время высокоэффективных насадок [1,4] каких либо сведений по расчету тепло-массообмена не имеется.
При противоточном движении в слое насадки жидкостного и газового потоков в зависимости от соотношения их расходов возможно существование различных гидродинамических режимов [3], поэтому математическая модель для оросителей градирни должна быть обобщенной, учитывающей охлаждение воды при одновременном ее течении в виде потоков капельного и пленочного течения через ороситель. Такая обобщенная модель может быть представлена в виде дискретного процесса состоящего из чередующейся последовательности актов появления капель и коротких участков пленки воды, их непродолжительного самостоятельного существования и последующего слияния соседних капель и пленок в пределах некоторого микрообъема. В результате интенсивного перемешивания в пределах образовавшегося микрообъема происходит выравнивание температуры жидкости, затем микрообъем разрушается с образованием новых капель и пленок жидкости для следующего акта и так далее. При контактировании капель и пленок жидкости с воздухом в пределах времени существования последовательного чередующихся актов и происходит охлаждение воды. Общее количество отобранной от воды теплоты определяется суммированием ее количества отобранного в дискретных капельном и пленочном потоках. При этом предлагается охлаждение капель и пленок воды для их дискретных потоков заменить ее охлаждением в эквивалентных по количеству отобранной теплоты в капельном и пленочном потоках, в которых капли и пленки охлаждаются при непрерывном перемещении в пределах оросителя при изменении параметров процесса в границах, определяемых условиями работы градирни. В таких потоках достигаемая температура охлаждения воды может быть рассчитана как для непрерывно осаждающейся одиночной капли и непрерывно стекающей пленки, обдуваемых воздухом за время, равное времени пребывания воды в оросителе за исключением времени, затрачиваемом на межактные процессы образования и разрушения совместных микрообъемов капельных и пленочных потоков жидкости. Задача об охлаждении воды при пленочном течении через ороситель подробно рассмотрена в работе [2], но решений об охлаждении капельного потока с учетом особенностей изменения параметров тепломассобменного процесса в пределах оросителя не имеется. В настоящей работе рассматривается такая задача.
Пусть одиночная капля воды обдувается потоком воздуха и температура воды в капле выше температуры воздушного потока. Тепловой поток от капли в некоторый момент ее охлаждения за элементарное время dτ определяется как:

где 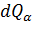 и
и 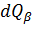 – тепловые потоки, соответственно, за счет теплоотдачи и за счет испарения, без учета теплоты, отводимой от капли вместе с массой потока пара, определяется как
– тепловые потоки, соответственно, за счет теплоотдачи и за счет испарения, без учета теплоты, отводимой от капли вместе с массой потока пара, определяется как
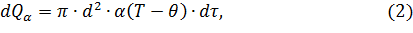
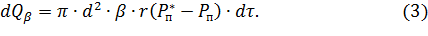
После подстановки этих значений потоков в уравнение (1), получаем

Этот же тепловой поток можно определить и как

Из совместного решения уравнения (4) и (5) получаем

Величину можно определить и как
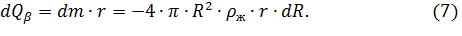
где dm— масса воды, испаренной за время dτ.
Из совместного решения уравнения (3) и (7) следует

Уравнение (8) в дифференциальной форме отражает взаимосвязь между переменными значениями времени испарения капли и ее радиуса. Интегрируя это уравнения для граничных условий, когда τ=0, то  и когда текущему времени процесса испарения капли τ соответствует текущие значение ее радиуса R, получим уравнение для определения этого радиуса для заданного времени испарения капли
и когда текущему времени процесса испарения капли τ соответствует текущие значение ее радиуса R, получим уравнение для определения этого радиуса для заданного времени испарения капли
- 
В градирне, в результате интенсивного перемешивания охлаждаемой воды в оросителе можно пренебречь различием температуры на поверхности капель и в их глубине и в пределах всей капли считать ее равной средней температуре воды по сечению потока воды в оросителе и тогда, в соответствии с условием Стефана, парциальное давление паров воды в диффузионном пограничном слое капли можно принять равным давлению насыщенного пара при этой температуре  [2] и тогда движущая сила массопередачи определится как
[2] и тогда движущая сила массопередачи определится как 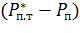 .
.
Движущая сила массопередачи 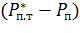 переменна по высоте оросителя и изменяется нелинейно вследствие нелинейной зависимости парциального давления от температуры. При выполнении инженерных расчетов ее можно усреднить, определяя как среднюю логарифмическую величину
переменна по высоте оросителя и изменяется нелинейно вследствие нелинейной зависимости парциального давления от температуры. При выполнении инженерных расчетов ее можно усреднить, определяя как среднюю логарифмическую величину 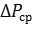 между значениями разностей
между значениями разностей 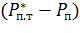 , найденных для крайних сечений оросителя. При этом значения парциальных давлений насыщенного пара
, найденных для крайних сечений оросителя. При этом значения парциальных давлений насыщенного пара  принимаются как для мокрого термометра при начальной и конечных температурах воды. Парциальное давление пара в воздушном потоке через ороситель переменно вдоль оросителя. При оценке работы оросителя его значение на выходе воздуха из градирни можно определить как
принимаются как для мокрого термометра при начальной и конечных температурах воды. Парциальное давление пара в воздушном потоке через ороситель переменно вдоль оросителя. При оценке работы оросителя его значение на выходе воздуха из градирни можно определить как
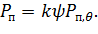
где 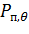 — парциальное давление насыщенного пара при температуре поступающего в градирню воздуха;
— парциальное давление насыщенного пара при температуре поступающего в градирню воздуха;
ψ — относительная влажность воздуха;
k — коэффициент, учитывающий увеличение относительной влажности воздуха по высоте оросителя. Его величина в зависимости от режима работы оросителя может изменяться в пределах 0,1 ¸0,4.
После усреднения движущей силы уравнение (9) запишется как

Постановка значения текущего радиуса определяемого выражением (10) в уравнение (6) приводит к дифференциальному уравнению
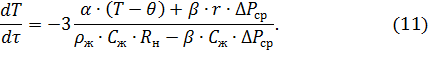
В результате решения этого дифференциального уравнения можно получить расчетное уравнение для определения изменения температуры капли заданного диаметра от времени ее непрерывного испарения в воздушном потоке при рабочих условиях оросителя. Влияние скорости обдува капли воздухом учитывается в этом уравнении неявно через зависимый от скорости воздушного потока коэффициент массоотдачи.
Для решения уравнения (11) представим его в форме зависимости

с комплексными параметрами равными:

Зависимость (12) при использовании новых переменных
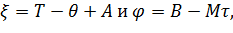
Обращается в дифференциальное уравнение,

решение, которого для граничных условий
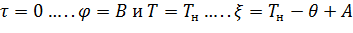
и позволяет получить искомое расчетное уравнение для определения температуры испаряющейся капли от времени испарения в виде зависимости

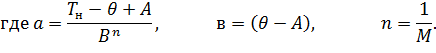
Рисунок 1. Зависимость температуры в капле от времени испарения
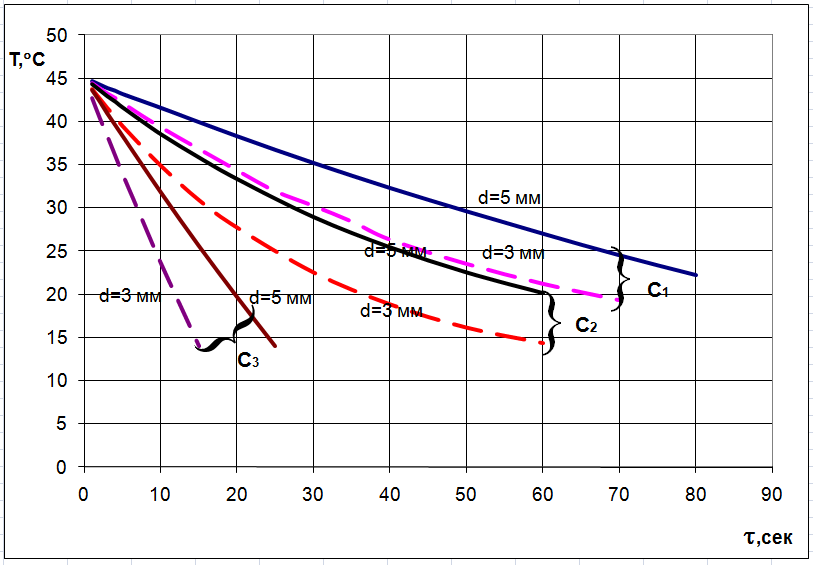
На рис. 1 представлены полученные с помощью уравнения (14) графики зависимости температуры воды в капле с начальным диаметром 3 и 5 мм от времени ее охлаждения для разных значений предложенного Льюисом коэффициента  , определяющего постоянство отношений между коэффициентом тепло — и массоотдачи при изменяющихся температуре и влагосодержании воздуха в градирне. При выполнении расчетов значения коэффициентов тепло — и массоотдачи принимались в пределах
, определяющего постоянство отношений между коэффициентом тепло — и массоотдачи при изменяющихся температуре и влагосодержании воздуха в градирне. При выполнении расчетов значения коэффициентов тепло — и массоотдачи принимались в пределах  .
.
Таким образом, предложена структура обобщенной модели для тепло-массообменного процесса в оросителе градирни при капельно-пленочном потоке воды. Получены входящие в состав обобщенной математической модели дифференциальное и расчетное уравнения, позволяющие определять температуру охлаждения воды для эквивалентного капельного потока, протекающий через ороситель воды.
Обозначения
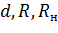 — диаметр, текущий и начальный радиус; T,θ — температура воды в капле и потоке воздуха; α,β — коэффициент тепло — и массоотдачи; r — удельная теплота испарения;
— диаметр, текущий и начальный радиус; T,θ — температура воды в капле и потоке воздуха; α,β — коэффициент тепло — и массоотдачи; r — удельная теплота испарения; — плотность и теплоемкость воды;
— плотность и теплоемкость воды;  — общее и парциальное давление пара в потоке воздуха;
— общее и парциальное давление пара в потоке воздуха; 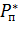 - парциальное давление пара в диффузионном пограничном слое;
- парциальное давление пара в диффузионном пограничном слое; 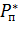 т — давление насыщенного пара при температуре воды в поперечном сечении оросителя;
т — давление насыщенного пара при температуре воды в поперечном сечении оросителя; 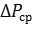 — средняя движущая сила массоотдачи в пределах оросителя.
— средняя движущая сила массоотдачи в пределах оросителя.
Список литературы:
- Боев Е. В., Иванов С. П., Афанасенко В. Г. Совершенствование конструкций полимерных оросителей градирен с целью повышения эффективности процесса охлаждения воды // Химическая промышленность сегодня. —2009. —№ 12. —С. 30‑34.
- Гладков В. А., Арефьев Ю. И., Пономаренко В. С. Вентиляторные градирни, М. : Стройиздат, 1976. —216 с.
- Кафаров В. В. Основы массопередачи : учеб. для студентов вузов. М. : Высшая школа, 1979. —439 с.
- Пушнов А. С. Керамические регулярные насадки для тепло-массообменных процессов в аппаратах защиты окружающей среды // Интенсификация технологических процессов: материалы, технологии, оборудование. —2009. —№1. —С. 16‑19.
дипломов


Оставить комментарий