Статья опубликована в рамках: I Международной научно-практической конференции «Научное сообщество студентов: МЕЖДИСЦИПЛИНАРНЫЕ ИССЛЕДОВАНИЯ» (Россия, г. Новосибирск, 06 декабря 2011 г.)
Наука: Технические науки
Секция: Металлургия
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ТЕПЛОВОГО ИЗЛУЧЕНИЯ НАКЛОННЫХ ЭЛЕКТРИЧЕСКИХ ДУГ НА ПОВЕРХНОСТЬ ВАННЫ ДСП
В ДСП ток протекает по трем параллельным графитированным электродам от одного электрода к другому, при этом направление протекания тока изменяется на 900, вследствие чего возникает электродинамическое усилие и эффект выдувания дуги из-под электрода. Ось дуги θ располагается под углом к оси графитированного электрода. Средний угол наклона столба дуги по отношению к нормали зеркала ванны колеблется для ДСП различной мощности и емкости в пределах 45‑65 градусов [1, с. 96].
Рассматривается модель падающего теплового потока от электрических дуг, расположенных под углом к тепловоспринимающей поверхности, на линию, образованную пересечением поверхности ванны и перпендикулярной ей плоскости, проходящей через ось дуг.
Рассмотрим модель теплового излучения на поверхность расплава от дуги одного электрода. На рисунке 1 показаны основные геометрические характеристики при горении электрической дуги Ιδ длиной между графитированным электродом и расплавом. Угол θ образован лучом ОВ, являющимся нормалью к тепловоспринимающей поверхности и лучом ОА, являющимся осью электрической дуги. Введем прямоугольную систему координат xOz, где ось z совпадает с осью дуги, а ось x находится в плоскости AOB.
Интенсивность облучения некой площадки поверхности посредством точечного цилиндрического излучателя мощностью dP можно определить как [2, с. 39]
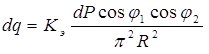 , (1)
, (1)
где R=|AC| — расстояние от источника излучения до центра площадки, Кэ — поправочный экспериментальный коэффициент, учитывающий долю мощности дуги, идущую на излучение, φ1 — угол между нормалью к оси дуги и направлением излучения, φ2 — угол между нормалью к поверхности ванны и направлением излучения. Рассмотрим тепловой поток облучения dq, падающий от источника излучения на площадку dS (рисунок 2). Видно, что 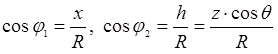 ,
,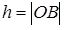 ,
,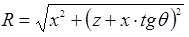 .
.
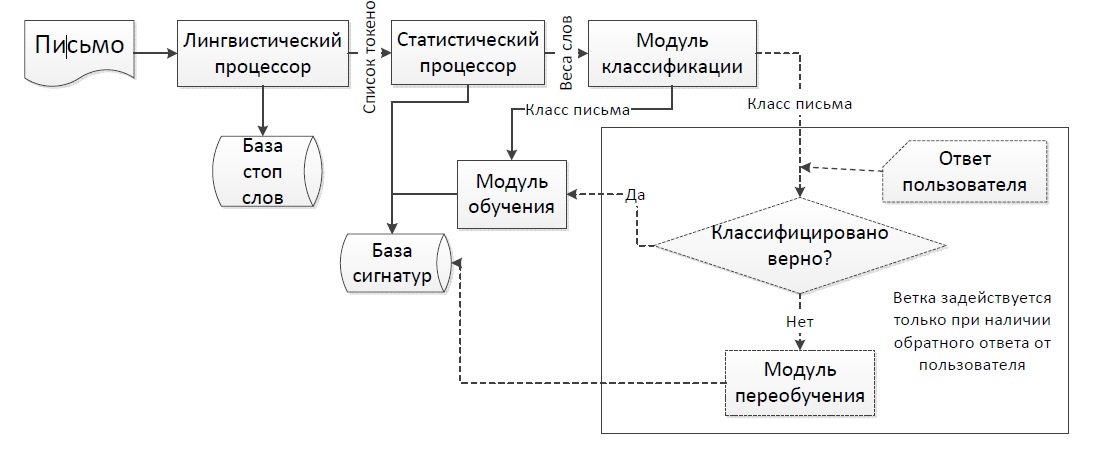

Рисунок 1. К расчету плотности теплового излучения дуги на минимальную площадку dS
Заменяя x=r * cosθ, получим
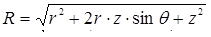 . (2)
. (2)
Считаем, что полная мощность излучения P дуги равномерно распределена по ее длине, поэтому в малом элементе объема дуги 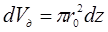 выделяется мощность
выделяется мощность  .
.
Получим, что:
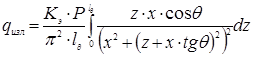 ,
,
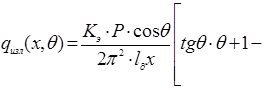
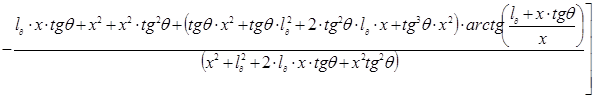 .
.
Приведем полученную зависимость теплового потока от расстояния вдоль луча OC (в направлении r)
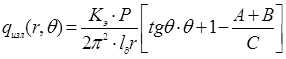 , (3)
, (3)
где 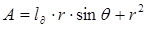 ,
,
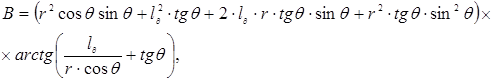 .
.
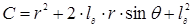
Значение теплового потока можно выразить в зависимости от безразмерного расстояния 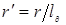
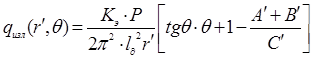 , (4)
, (4)
где 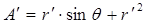 ,
,
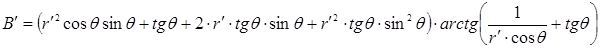 ,
,
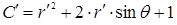 .
.
Рассмотрим теперь тепловой поток облучения, падающий от источника dq в точку C' (рисунок 1). Все рассуждения по определению теплового потока остаются без изменения за исключением того, что расстояние R будет определяться как 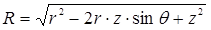 .
.
Так как функция sin θ нечетная, поэтому -sin θ=sin (-θ), следовательно, для площадки dS', расположенной на отрезке , имеем такое же решение (3) ‑ (4), как для отрезка OC', если подставить .
Необходимо отметить, что выражение (3) после несложных преобразований переходит в формулу, полученную для дуги, ось которой совпадает с нормалью ( θ=0)
 . (5)
. (5)
Рассмотрим теперь модель теплового потока на произвольно расположенную площадку dS находящуюся на поверхности ванны от электрической дуги, расположенной под углом к ней.
Введем декартову систему координат Oxyz, связанную с центром привязки дуги, причем плоскость Oxy совпадает с поверхностью ванны, а начало координат O является пересечением оси дуги OA и поверхности ванны (рисунок 2). Ось электрической дуги находится в плоскости Oxz. Положение площадки dS задается ее расстоянием r от точки O и углом ψ. Вектор перпендикулярен площадке dS, а вектор лежит в плоскости AOC и перпендикулярен прямой OA. В выбранной декартовой системе имеем координаты точек: C(r cos ψ, r sin ψ, 0); A(‑z0 sin θ; 0; z0 cos θ).
Для определения углов φ1 и φ2, используя векторную алгебру, напишем координаты основных векторов:
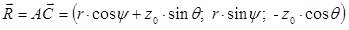 ;
;
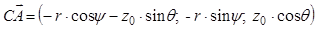 ;
;
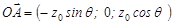 ;
;  ;
;
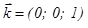 .
.
Найдем расстояние от источника излучения до центра dS
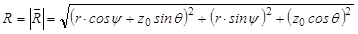 , упрощая, получим
, упрощая, получим
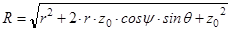 . (6)
. (6)
Определим косинусы углов
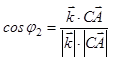 =
= 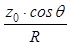 , (7)
, (7)
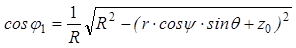 .
.
Подставив в последнее выражение значение R2, получим
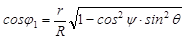 . (8)
. (8)
С учетом соотношений (6‑8), интегрируя, получим тепловой поток в точке С от излучения всей дуги:
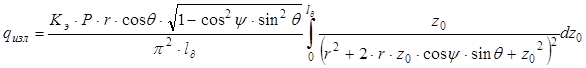 или
или
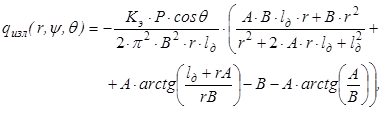 (9)
(9)
где 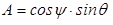 ;
; 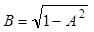 .
.
Рисунок 2. К расчету плотности теплового излучения дуги на площадку dS
Иллюстрируя полученную модель, приведены зависимости теплового излучения одной дуги от угловой координаты ψ, при разных углах наклона дуги θ (рисунок 3). Видно наличие плоскости зеркальной симметрии Oxz, при этом минимальное значение теплового потока наблюдается при ψ=00, а максимальное – вблизи направления ψ =1800.
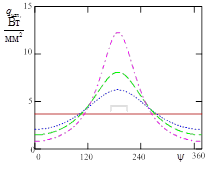
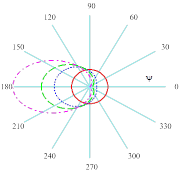 а б
а б
Рисунок 3. Тепловой поток вдоль азимутальной координаты точки привязки дуги : а – линейный график; б – полярный график; угол наклона дуги: – θ=00; – θ=200; – θ=300; – θ=450
Переходим к модели теплового потока при одновременном горении трех дуг. Рассмотрим декартову систему координат Oxyz, началом которой является центр распада электродов (рисунок 4). Плоскость Oxy совпадает с поверхностью ванны, ось Ox проходит через центр первого электрода, а ось электрической дуги находится в плоскости Oxz.
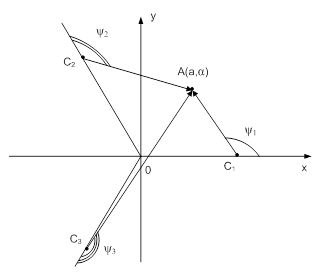
Рисунок 4. К расчету плотности теплового излучения дуги на площадку dS
Тогда центры привязки дуг с учетом их отклонения от нормали имеют следующие координаты:
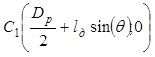 ,
,
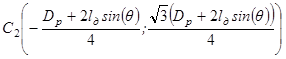 ,
,
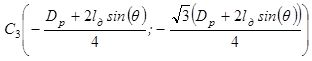 ,
,
где Dp – диаметр распада электродов.
Находим тепловой поток в точке A(acosα;:asinα), которая является центром площадки dS. Векторы, проходящие через центры привязки дуг и точку A, имеют координаты 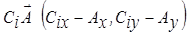 , а их длина
, а их длина  , где i‑1, 2, 3.
, где i‑1, 2, 3.
Определим углы ψi, показанные на рисунке 4:
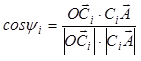 .
.
Зная ri и cosψi, запишем суммарный тепловой поток, падающий на элементарную площадку как сумму тепловых потоков, от каждой из дуг
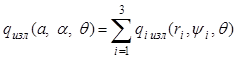 . (10)
. (10)
Таким образом, создана математическая модель распределения теплового потока на поверхность ванны ДСП от одной и трех наклонных электрических дуг. Установлено, что, при отклонении электрической дуги от нормали к поверхности ванны падающий тепловой поток перестает быть осесимметричным; в направлениях ψ=900 и ψ =2700 тепловой поток не зависит от угла наклона дуги θ; в распределении тепловых потоков имеет место зеркальная симметрия относительно плоскости, проходящей через ось дуги и перпендикулярной поверхности ванны.
Список литературы:
- Макаров А.Н. Теплообмен в дуговых сталеплавильных печах. — Тверь: ТГТУ, 1998. — 184 с.
- Макаров А.Н., Свенчанский А.Д. Оптимальные тепловые режимы дуговых сталеплавильных печей. — М.: Энергоатомиздат, 1992. — 96 с.
- Ячиков И.М., Портнова И.В. Взаимодействие колеблющейся дуги с поверхностью расплава / И.М. Ячиков, И.В., Портнова // Наука и технологии. Том 1. Труды XXIV Российской школы по проблемам науки и технологий, посвященной 80-летию со дня рождения академика В.П. Макеева. —М., 2004. — С. 224–230.
дипломов


Оставить комментарий