ИНТЕРАКТИВНЫЕ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ ЧИСЛЕННЫМИ МЕТОДАМИ АЛГЕБРЫ

Современный этап развития общества характеризуется интенсивной математизацией знаний. Это проявляется в том, что математические методы все больше проникают во все сферы жизнедеятельности людей: в науку, в производство, в технику, в экономику и т. д. Связь математики с деятельностью человека имеет тенденцию к усложнению, становится многоступенчатой. При этом, чем шире и разнообразнее практическая деятельность людей, тем выше требования к математической подготовке студентов вузов, как будущих специалистов.

Одним из перспективных направлений развития технологий обучения является дистанционное обучение. В связи с интенсивным развитием информационных технологий, и особенно интернет-технологий, проблема развития дистанционного обучения приобретает особую значимость.

Дистанционное (дистантное) обучение — это обучение на расстоянии, при котором преподаватель и обучаемые физически находятся в различных местах. Изначально дистанционное обучение отождествлялось, как правило, с заочным обучением. Однако сейчас — это средство обучения, использующее аудио, видеотехнику, интернет и спутниковые каналы связи.

К преимуществам дистанционной формы обучения можно отнести: обучение в психологически комфортной, привычной для вас обстановке за вашим компьютером; индивидуальные сроки и темп обучения; высокая доля самостоятельности наряду с возможностью в любое время получить помощь от преподавателя; преодоление территориальных и временных ограничений [9].

Дистанционное образование тесно связанно с дистанционным обучением.

Принято считать, что дистанционное образование — это процесс передачи знаний (за него ответственен преподаватель и школа), а дистанционное обучение — это процесс получения знаний (за него ответственен ученик) [9].

Покажем использование информационных технологий в учебном процессе на примере изучения одной из учебных дисциплин, в частности дисциплины «Методы численного анализа».

Целью изучения курса «Методы численного анализа» является освоение основных идей методов численного решения прикладных задач, областей их применения и методики их использования при проектировании и разработке систем математического обеспечения, обработке данных задач, построении алгоритмов и организации вычислительных процессов на персональных компьютерах. Актуальность данного исследования обусловлена: потребностью в решении математических задач на машинах без установленного специального ПО; потребностью в единой теоретической базе по вычислительным методам.

Цель нашего проекта: создать простой, удобный и одновременно функциональный сайт, позволяющий быстро решать нелинейные уравнения и их системы в режиме онлайн.

Задачи исследования: продемонстрировать интерактивное пошаговое решение нелинейных уравнений различными методами; предоставить теоретическую базу демонстрируемых методов; внедрить ресурс в учебный процесс.

Общее описание информационного ресурса. Создание ресурса велось на базе веб-сервера Apache (версия 2.2.21) при помощи сборки XAMPP (версия 1.7.7) для платформы Ubuntu Linux (версия 11.10, версия ядра 3.0.0-12-generic) и XAMPP (версия 1.5.4) для платформы MS Windows 7 (версия 6.1, Build 7601: SP1) [1].

Алгоритмы вычислительных методов, системы ввода данных и генерации других динамических страниц реализованы на скриптовом языке программирования PHP (версия 5.3.8) [2].

Верстка сайта осуществлялась при помощи языка разметки гипертекста HTML и каскадных таблиц стилей CSS [3, 4, 5, 6, 7, 8].

Отладка и тестирование готового ресурса осуществлены при помощи веб-браузеров Mozilla Firefox (версии 7.0.1 и 8.0), Google Chrome (версия 16.0.912) и Chromium (версия 15.0.860.0), Opera (версия 11.52) и Internet Explorer (версии 7.0 и 9.0).

Внешний вид сайта (рис. 1) реализован на языке HTML в виде шаблона, что значительно облегчает доступ к различным его разделам, а также уменьшает объем кода.

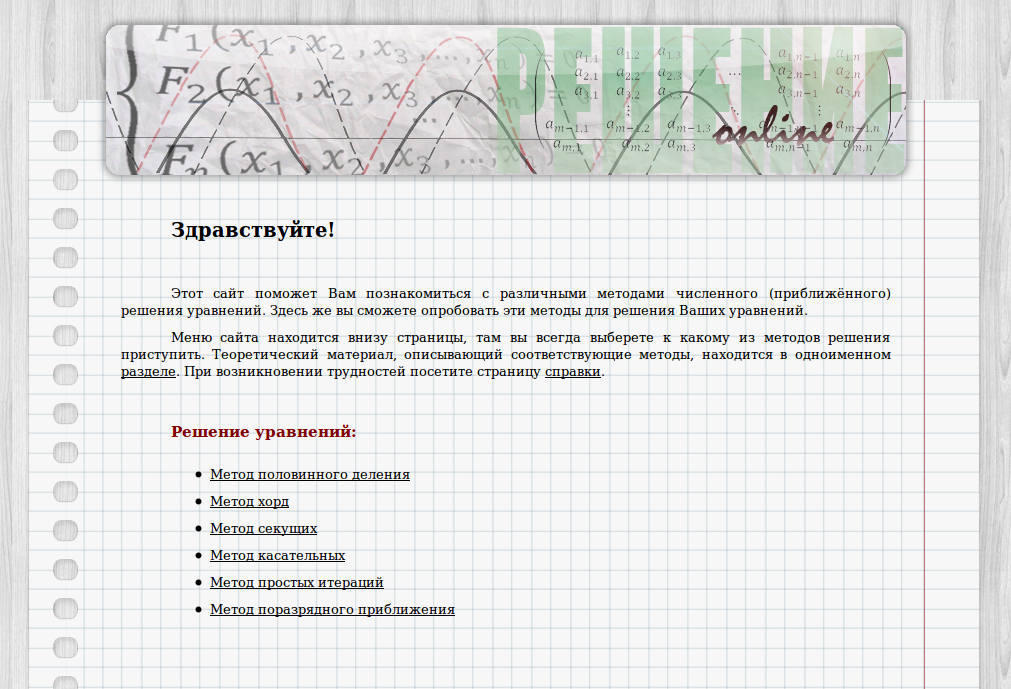
Рисунок 1. Главная страница веб-сайта.

Веб-сайт содержит раздел теоретической информации, предоставляющий пользователю подробные теоретические данные о сути методов и принципах действия их алгоритмов (рис. 2).

Рисунок 2. Раздел «Теоретические материалы».

Простой и конструктивный интерфейс реализован на принципе пошагового подхода к решению уравнений, а именно позволяет получить решение нелинейного уравнения всего за 5 простых шагов.

Пользователю предоставляется возможность выбора используемого метода и сопровождающие комментарии, предоставляющие информацию о том, что нужно делать на том или ином шаге. Раздел справки предоставляет информационную помощь пользователю в случаях возникновения трудностей во время использования ресурса. Информационный ресурс позволяет наглядно получить представление об особенностях работы различных методов решения нелинейных уравнений.

Описание работы ресурса для решения уравнения. Работу созданного веб-ресурса рассмотрим на примере одного из методов.

Постановка задачи: решим уравнение 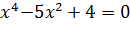  методом половинного деления.

Решение.

1. На первом шаге пользователю предлагается ввести старшую степень многочлена вида a₀xⁿ + a₁x^n-1 + a₂x^n-2 + ... + a_n-1x¹ + a_nx⁰ = 0, где

x – неизвестная переменная; a₀, ..., a_n – коэффициенты при переменной (рис. 3). В нашем случае введем n = 4:

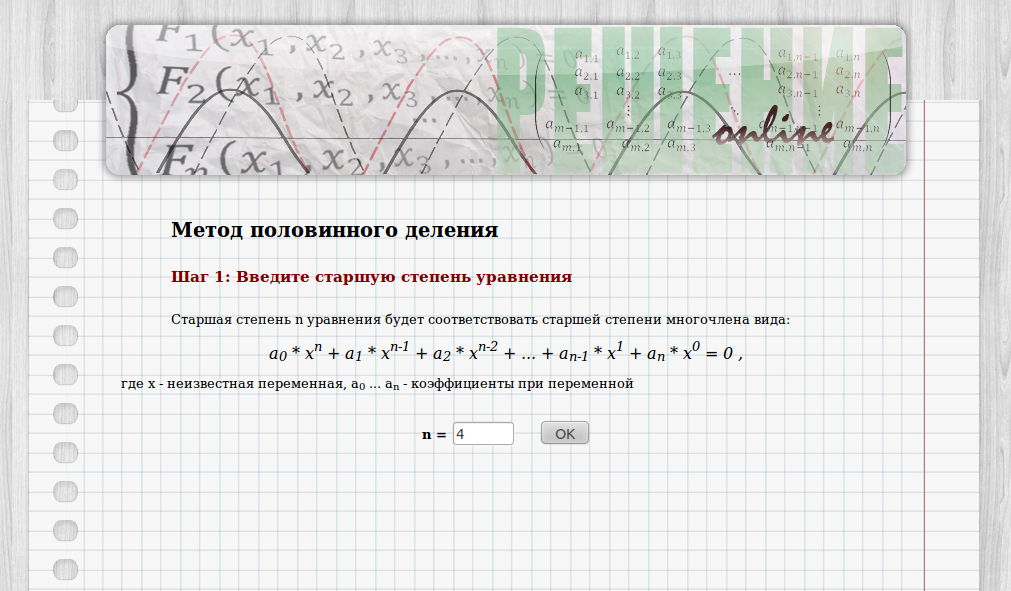
Рисунок 3. Введение старшей степени уравнения.

2. На следующем шаге пользователю предлагается ввести коэффициенты при различных степенях неизвестной переменной x в соответствующие поля формы (рис. 4). Заполним поле: a₀ = 1, a₂ = –5, a₄ = 4, а оставшиеся коэффициенты оставим нулевыми:

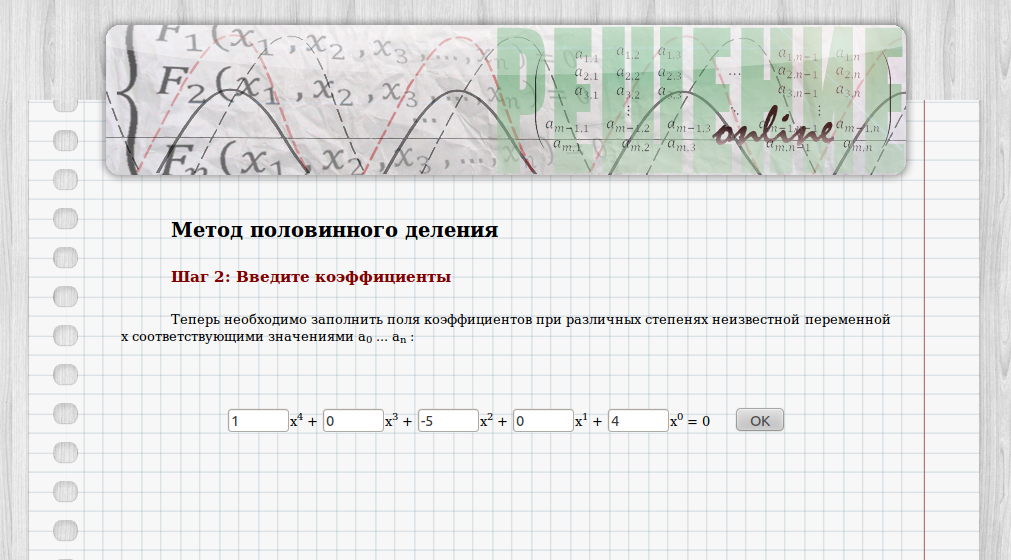
Рисунок 4. Введение коэффициентов.

3. Теперь необходимо задать промежуток [a; b], содержащий неизвестную переменную x. На заданном промежутке будет построен график функции, соответствующей введенному ранее уравнению. Таким образом возможно отделить корни в случае существования более одного решения уравнения, и визуально выбрать интервалы для дальнейшего уточнения отдельных корней (рис. 5). В нашем случае зададим отрезок [– 10; 10]:

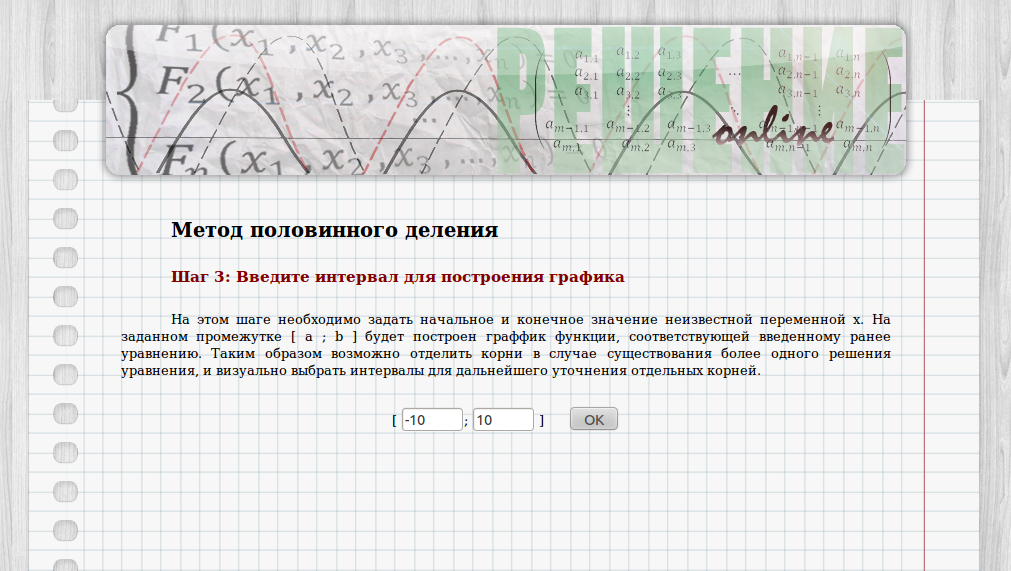
Рисунок 5. Введение промежутка для построения графика функции.

4. Пользуясь построенным графиком, который соответствует введенному уравнению, необходимо установить более узкий интервал, на котором будет уточняться корень. Стоит учитывать, что на вводимом интервале должен быть один и только один корень, то есть график функции должен единожды пересекать ось абсцисс (рис. 6).

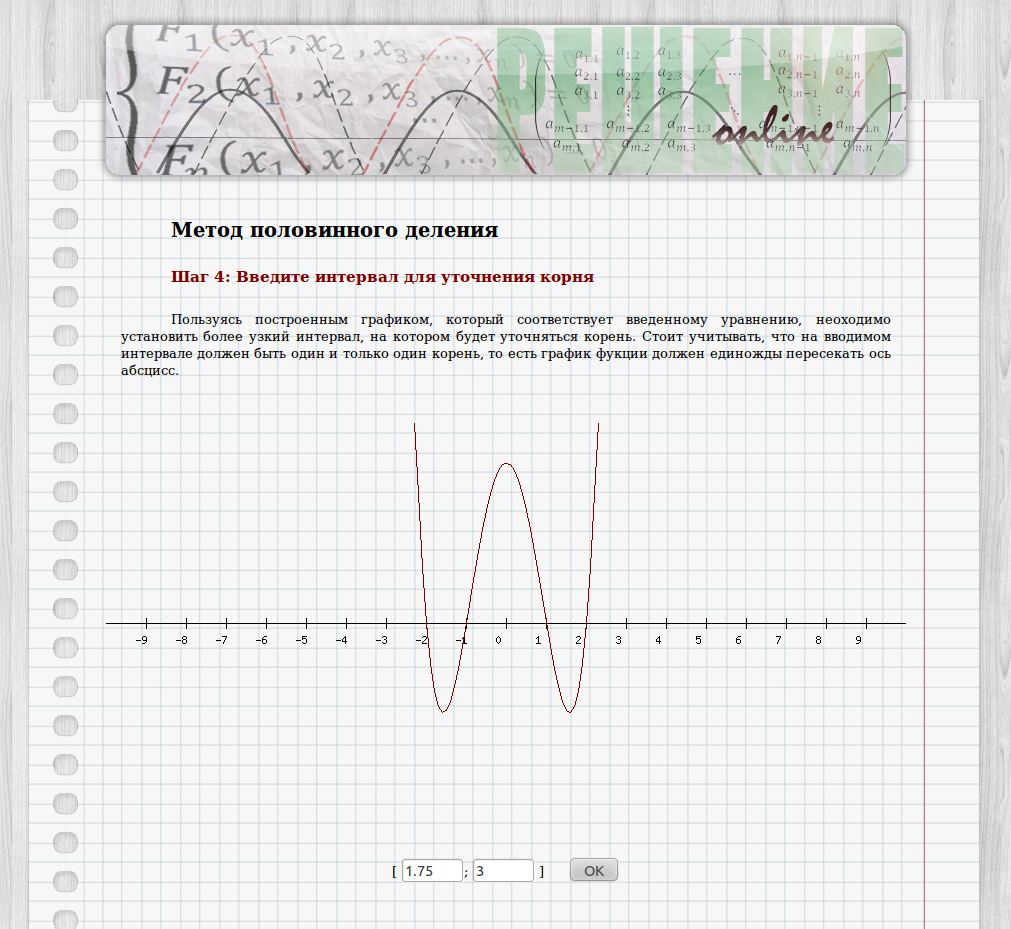
Рисунок 6. График функции.

Замечаем, что в нашем случае график пересекает ось 4 раза, что соответствует количеству действительных корней уравнения. Выберем один промежуток для уточнения корня: [1,75; 3].

5. Далее требуется ввести число ε, которое задает точность производимых вычислений. Процесс уточнения корня будет считаться завершенным, когда модуль разности между x_i (вычисленным приближением на текущей итерации) и x_i-1 (вычисленным приближением на предыдущей итерации) не будет превышать заданного предела точности (рис. 7). Зададим ε = 0,0001:

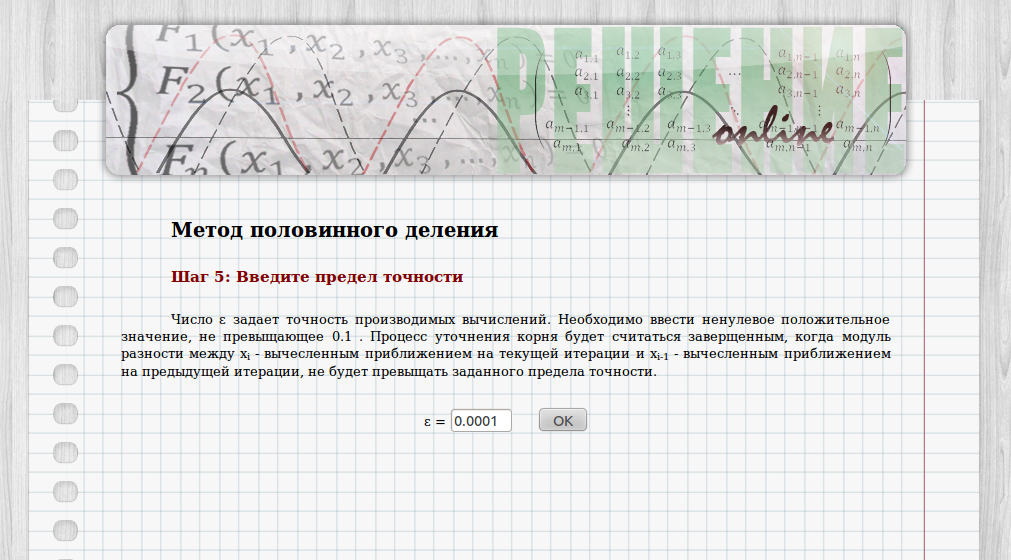
Рисунок 7. Введение предела точности вычислений.

6. Все необходимые параметры для работы метода введены и по нажатию кнопки ОК пользователь получит численное решение с точностью до ε (рис. 8).

Рисунок 8. Результат решения уравнения.

Итоги. Результаты тестирования показали, что сайт работает корректно во всех предлагаемых ситуациях. Промежуточные результаты работы над проектом обсуждались на научно-практической студенческой конференции гуманитарного факультета БГУ. Созданный ресурс используется в учебном процессе студентами 3 курса специальности «Информатика» для решения практических задач, а также для самообразования и самоконтроля.

Ресурс расположен в сети интернет на сервере университета и доступен для прямого использования по адресу http://gumf.bsu.by/nelur/

Данный информационный портал может быть использован студентами, учащимися старших классов, а так же всеми пользователями, которые сталкиваются с проблемой численного решения нелинейных уравнений.

Продолжая работу над проектом, мы намерены расширить созданную нами информационно-справочную систему, в частности: дополнить ресурс методами, позволяющими решать системы линейных и нелинейных уравнений, задачи алгебраической интерполяции, задачи численного дифференцирования и интегрирования в режиме онлайн.

Список литературы:

1. Бабушкин М. Web-сервер в действии. Издательский дом «Питер», Санкт-Петербург, 2005. — 272 с.
2. Григин И. Е. PHP 5.1. Руководство программиста. Издательский дом «Питер», Санкт-Петербург, 2006. — 496 с.
3. Комолова Н. В. HTML: учебный курс. Издательский дом «Питер», Санкт-Петербург, 2007. — 272 с.
4. Лещев Д. В. Создание интерактивного web-сайта. Учебный курс. Издательский дом «Питер», Санкт-Петербург, 2003. — 544 с.
5. Макфарланд Д. Большая книга CSS. Издательский дом «Питер», Санкт-Петербург, 2010. — 512 с.
6. Ташков П. А. Веб-мастеринг на 100 %: HTML, CSS, JavaScript, PHP, CMS, AJAX, раскрутка. Издательский дом «Питер», Санкт-Петербург, 2011. — 512 с.
7. Фримен Э. Изучаем HTML, XHTML и CSS. Издательский дом «Питер», Санкт-Петербург, 2010. — 656 с.
8. Хеник Б. HTML и CSS: путь к совершенству. Издательский дом «Питер», Санкт-Петербург, 2011. — 336 с.
9. Хуторской А. В. Современная дидактика: учебник для вузов. Cерия «Учебник нового века». Изд. «Питер», Санкт-Петербург, 2001. — 608 с.