РЕШЕНИЕ  УРАВНЕНИЯ  ТИПА  ВОЛНОВОГО  ПРИ  МОДЕЛИРОВАНИИ  ДВИЖЕНИЯ  ОБЪЕКТА  В  ПОТЕНЦИАЛЬНОМ  ПОЛЕ  СИЛ

Яковлев  Антон  Сергеевич

Костомарова  Татьяна  Васильевна

студенты  4  курса  каф.  спецматематики,  КНИТУ-КАИ,  РФ,  г.  Казань

Валишин  Наиль  Талгатович

научный  руководитель,  канд.  физ.-мат.  наук  доцент,  КНИТУ-КАИ,  РФ,  г.  Казань

E-mail:  vnailt@yandex.ru

Из  формулировки  локального  вариационного  принципа  (ЛВП)  и  новой  постановки  прямой  и  обратной  задачи  динамики  и  нового  продолжения  оптико-механической  аналогии  (метод  V-функции)  [1,  3]  следует,  что  траекторное  движение  объекта,  описываемое  системой  уравнений

,                        (1)

где    —  вектор  фазовых  координат,  ,  сопряжено  волновым  движением,  удовлетворяющим  уравнению

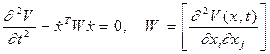  (2)

где    —  однозначная,  кусочно-непрерывная  функция  (,).  Уравнение  (2)  следует  рассматривать  с  граничными  и  начальными  условиями  для  волны  и  траектории  объекта

  (3)

  (4)

,  (5)

,  (6)

Следует  также  отметить,  что  такая  постановка  траекторно-волнового  движения  объекта  тесно  связано  с  исследованиями  Б.Н.  Родимова  [2].

Рассматриваются  линейный  гармонический  осциллятор  и  движение  объекта  (электрона)  в  водородоподобном  атоме.  В  первом  случае  уравнение  траекторного  движения  объекта  (частицы)

                      (7)

допускает  первый  интеграл  .

Отсюда  получаем  выражение  для  квадрата  скорости  частицы  вида

.     (8)

Подставив  (8)  в  уравнение  (2)  (n=1),  получим:

  (9)

Волновая  функция  V (x,t)  ищется  в  виде  .  В  результате  из  уравнения  (9)  получим  следующее  стационарное  уравнение:

  (10)

Начальные  условия  для  функции  и,  получаются  в  виде:

    (11)

Как  видно  из  уравнения  (10)  решение  ,  должно  удовлетворять  естественному  условию, 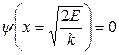 .  Выполнение  этого  условия  возможно  лишь  при  конкретных  значениях  собственных  частот  уравнения  (10).  Введем  безразмерную  величину  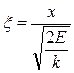,  тогда  уравнение  (10)  принимает  вид

,  (12)

где  .

Определим  эти  частоты  численно  из  решения  уравнения  (10)  с  начальными  условиями  (11).  Для  этого  введем  вспомогательные  функции 

;

.

и  будем  решать  систему

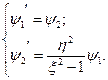
методом  Рунге-Кутта  четвертого  порядка,  с  начальными  значениями 

.  Получим

      …

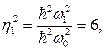
С  учетом  результатов  оптико-механической  аналогии  [1,  3]  мы  получаем  правило  квантования  энергии  гармонического  осциллятора  в  следующем  виде

  (13)

Значит  в  случае,  когда  траекторное  движение  объекта  непосредственно  связано  с  волновым  движением,  энергия  гармонического  осциллятора  может  принять  только  определенные  дискретные  значения:        Данные  значения  получаются  также  аналитически  с  помощью  программного  комплекса  Maple 

и  в  виде  ряда

Как  известно,  Шредингер  получил  правило  квантования  энергии  для  гармонического  осциллятора  в  виде  .  Если  эти  результаты  подставить  в  равенство  (13)  мы  будем  иметь 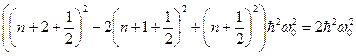 ,  т.  е.  получаем  тождество. 

В  случае  движения  электрона  в  водородоподобном  атоме  уравнения  (1)  и  (2)  можно  также  свести  к  одному  уравнению  [1,  3]

,  (14)

где:    —  оператор  Лапласа, 

—  масса  объекта  (частицы), 

—  полная  энергия  объекта  (частицы), 

  —  потенциальная  энергия  водородоподобного  атома.

Применив  метод  разделения  переменных  к  уравнению  (14)  ,  получим  следующее  стационарное  уравнение

  (15)

где  .

В  уравнении  (15)  перейдем  к  сферической  системе  координат,  применим  также  метод  разделения  переменных    и  рассмотрим  уравнение  для  радиальной  составляющей:

  (16)

Если  в  (16)  сделать  замену  ,  то  получим

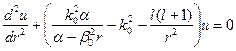,  (17)

где  .

Полученное  уравнение  (17)  при  l=0  решается  с  помощью  степенного  ряда.  Учитывая  асимптотическое  решение  уравнения  (17)  (),  можно  искать  частное  решение  в  виде  .  Подставив  его  в  (17)  при  l=0,  получим  следующие  уравнения:

,  (18)

где  . 

Рассмотрим  решение  уравнения  (18)  в  виде  следующего  степенного  ряда  .  После  подстановки  этого  решения  в  уравнение  (18),  оно  принимает  вид

,  (19)

Так  как  равенство  (19)  должно  выполняться  при  всех  степенях  ,  поэтому  ,  а  коэффициенты    удовлетворяют  рекуррентному  соотношению

      (20)

Ряд    обрывается,  т.  е.    при  ,  при  условии  ,  что  приводит  к  следующему  решению 

,  (21)

где  С  —  постоянная,            

Равенство  ,  с  учетом    и  .  приводится  к  виду  .  Отсюда,  учитывая  связь  частоты  и  энергии  который  вытекает  из  оптико-механической  аналогии  [1,  2],  находим  значение  энергии  n-го  состояния  электрона 

.     (22)

Отметим,  что  энергия  n-го  состояния  водородоподобного  атома  в  точности  совпадает  с  решением,  полученным  Бором  на  основе  своей  модели  [4]  или  Шредингерем  на  основе  своего  стационарного  уравнения  [5]. 

Так  как  уравнение  (17)  при  удовлетворяет  тем  же  значениям  энергии  как  и  при  ,  то  мы  можем  построить  решения  (17)  исходя  из  решения  данного  уравнения  при  для  соответствующих  значений  энергии.  Такие  решения  находились  численно.

Список  литературы:

1.Валишин  Н.Т.  Валишин  Ф.Т.,  Моисеев  С.А.  Траекторно-волновой  подход  к  динамике  электрона  в  атоме  водорода.  //  Бутлеровские  сообщения.  —  Т.  25.  —  №  5,  —  2011  г.  —  С.  1—12. 

2.Родимов  Б.Н.  Автоколебательная  квантовая  механика.  Физико-математическое  наследие:  физика  (квантовая  механика)  М.  2010  г.  —  416  с. 

3.Valishin  N.T.  Variational  principle  and  the  problems  dynamics  //  Life  Science  Journal  2014;11(8):  568—574,  2014.

4.Bohr  N.  On  the  constitution  of  atoms  and  molecules.  //  Philosophical  Magazine,  —  1913,  —  v.  26,  —  p.  1—25,  476—502,  857—875.

5.Schrödinger  E.  Quantisierung  als  Eigenwertproblem  //  (I  Mitt)  Annalen  der  Physik,  1926,  Bd  79,  S.  361—376;  (II  Mitt)  —  Ibid.,  S.  489—527;  (III  Mitt)  —  Ibid.,  Bd  80,  S.  437—490;  (4  Mitt)  —  Ibid.,  Bd  81.