Статья опубликована в рамках: XV Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ЕСТЕСТВЕННЫЕ НАУКИ» (Россия, г. Новосибирск, 28 января 2014 г.)
Наука: Физика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ФИЛЬТРАЦИОННО-ВОЛНОВЫЕ ПОЛЯ В ТРЕХСЛОЙНОЙ АНИЗОТРОПНОЙ СРЕДЕ
Насибуллина Эльвира Рустямовна
студент 2курса, кафедра химико-технологических процессов УГНТУ, РФ, Республика Башкортостан, г. Салават
E-mail: zamowa.guln@mail.ru
Заманова Гульназ Фаизовна
научный руководитель, ассистент кафедры ХТП, РФ, Республика Башкортостан, г. Салават
Аннотация. Найдены простые аналитические зависимости для расчета полей в неоднородных анизотропных пластах в нулевом приближении. Наличие таких зависимостей позволяет обеспечить основу для принципиально нового и более полного исследования волновых полей применительно к акустическому каротажу и сейсморазведке.
Ключевые слова: телеграфное уравнение, асимптотический метод, нулевой коэффициент разложения, волновое поле давления, точное решение.
Введение. Теоретические методы исследования волновых полей в пластах и скважине, по мнению ведущих специалистов, не отвечают в достаточной мере требованиям практики. Таким образом, развитие теории волновых полей в пласте и скважине представляет важнейшую проблему, имеющую большое практическое значение [3].
Ниже в нулевом приближении построено решение задачи о фильтрационных волновых полях в неоднородной анизотропной пористой среде путем использования «в среднем точного» асимптотического метода, идеи которого изложены в работах [2], [3], [4].
Показано, что фильтрационно-волновое поле в проницаемой однородной изотропной пористой среде описывается телеграфным уравнением [1]. Это позволяет использовать развитые ранее методы расчета для электромагнитных полей в линиях передачи для исследования фильтрационно-волновых полей в подземной гидродинамике. При устремлении скорости передачи упругих возмущений к бесконечности из полученных решений следует выражения, построение ранее на основе уравнений пьезопроводности [4].
Постановка задачи для линейной геометрии. На рис. 1 представлена геометрия течения в прямоугольной системе координат, ось zd которой совпадает с осью скважины. Пусть неоднородная среда представлена тремя областями с плоскими границами раздела zd = ±h, перпендикулярными вертикальной оси. Покрывающий и подстилающий пласты считаются слабопроницаемыми в горизонтальном направлении, средняя область толщины 2h (-h < zd < h) является хорошо проницаемой и в горизонтальном и в вертикальном направлениях. Для простоты течение полагается линейным (по горизонтальной оси xd). Окружающие породы являются сильно анизотропными, и в них преобладает вертикальная проницаемость в сравнении с горизонтальной настолько, что можно пренебречь членом со второй производной по горизонтальной координате xd в уравнении для окружающей среды.
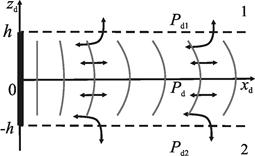
Рисунок 1. Геометрия задачи: 1 — покрывающая среда; 2 — подстилающая среда
Математическая постановка гидродинамической задачи в таких предположениях включает волновые уравнения, учитывающее преобладание вертикальной проницаемости, в верхнем и нижнем пластах:
|
|
|
|
|
|
волновое уравнение в центральном пласте:
|
|
|
В начальный момент времени возмущения давления отсутствуют:
|
|
|
На границе раздела сред заданы равенства давлений и потоков:
|
|
|
|
|
|
Давление на левой границе изменяется по гармоническому закону:
|
|
|
Для сопряженной комплексной части имеем следующую задачу:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Далее задачу (1.8)—(1.14) умножив на i и сложив с задачей (1.1)—(1.7)получим задачу для комплексного давления P .
С использованием соотношений:
|
|
где:![]() — атмосферное давление. Запишем задачу (1.7)—(1.14) в безразмерном виде:
— атмосферное давление. Запишем задачу (1.7)—(1.14) в безразмерном виде:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
||
|
|
||
|
|
||
Решение задачи (1.8) – (1.14) будем отыскивать в виде:
|
|
|
Задача для амплитуд давления представится в виде:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Предполагается, что решение является регулярным на бесконечности, т.е. при устремлении пространственных координат в бесконечность искомое решение, а при необходимости и его производная, обращается в нуль.
2. Разложение по асимптотическому параметру. Рассмотрим более общую задачу, полученную введением произвольного асимптотического параметра e перед первой и второй производными от функции возмущения давления в центральном пласте по z, как в уравнениях, так и в граничных условиях задачи:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В задаче (2.1)—(2.6) введены обозначения ![]() ,
, ![]() ,
, ![]() . Отметим, что решение исходной задачи может быть получено из решения параметризованной задачи при
. Отметим, что решение исходной задачи может быть получено из решения параметризованной задачи при![]() . Задача (2.1) – (2.6) является, таким образом, частным случаем более общей параметризованной, содержащей формальный параметр асимптотического разложения e.Решение задачи (2.1)—(2.6) будем искать, представляя функцию давления Р каждой из областей асимптотической формулой по параметру e:
. Задача (2.1) – (2.6) является, таким образом, частным случаем более общей параметризованной, содержащей формальный параметр асимптотического разложения e.Решение задачи (2.1)—(2.6) будем искать, представляя функцию давления Р каждой из областей асимптотической формулой по параметру e:
|
|
|
Подставив выражения (2.7) в (2.1) – (2.6) и сгруппировав слагаемые по степеням параметра разложения e, получим:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Анализ задачи показывает, что сомножители при степенях e в (2.9) содержат соседние коэффициенты разложения и в этом смысле являются «зацепленными». Для решения соответствующего уравнения осуществлена процедура расцепления.
3. Постановка задачи в нулевом приближении. Формально устремим e к нулю в уравнении (2.9) получим ![]() . Результат интегрирования
. Результат интегрирования ![]() , с учетом граничных условий (2.12) позволяет установить, что
, с учетом граничных условий (2.12) позволяет установить, что ![]() . Таким образом, в нулевом приближении давление является функцией только от x и не зависит от z:
. Таким образом, в нулевом приближении давление является функцией только от x и не зависит от z: ![]() , т. е. одинаково в каждой точке любого сечения, параллельного оси z.
, т. е. одинаково в каждой точке любого сечения, параллельного оси z.
Далее, приравнивая к нулю коэффициенты при e в уравнении (2.10), получим:
|
|
|
Так как P(0)(x) не зависит от переменной z, вспомогательная функция E(x), составленная из слагаемых уравнения (3.1), содержащих P(0):
|
|
|
также не зависит от z. Тогда (3.1) можно представить как:
|
|
|
Проинтегрировав последовательно, найдем выражения для первой производной от первого коэффициента P(1) по переменной z
|
|
|
и первого коэффициента разложения в виде квадратного трехчлена
|
|
|
с функциональными коэффициентами ![]() подлежащими определению. Из граничных условий (2.12) при сомножителе
подлежащими определению. Из граничных условий (2.12) при сомножителе ![]() в первой степени имеем:
в первой степени имеем:
|
|
|
Отсюда следуют выражение для функциональных коэффициентов ![]()
|
|
|
и![]()
|
|
|
через следы производных из внешних областей.
Подставив выражение (3.2) в (3.7), получим уравнение для определения нулевого приближения поля давления в пласте:
|
|
(3.9) |
Окончательная постановка задачи в нулевом приближении включает также уравнения в покрывающих и подстилающих породах:
|
|
|
|
|
|
а также соответствующие граничные и начальные условия:
|
|
(3.12) |
Выражения (3.9)—(3.11) представляют краевую задачу для нулевого коэффициента разложения ![]() или нулевого приближения. Отметим, что эта задача относится к неклассическим, поскольку уравнение для пласта содержит следы производных из внешних областей.
или нулевого приближения. Отметим, что эта задача относится к неклассическим, поскольку уравнение для пласта содержит следы производных из внешних областей.
Непосредственным интегральным усреднением исходной задачи нетрудно убедиться, что (3.9)—(3.11) представляет задачу для осредненных некоторым образом по толщине центральной зоны значений давления. Это определяет физический смысл нулевого коэффициента разложения или нулевого приближения и практическую важность его определения, поскольку поиском осредненных значений в подобного рода задачах чаще всего и ограничиваются.
4. Решение в нулевом приближении. Для решения задачи воспользуемся интегральным синус-преобразованием Фурье по переменной х:
|
|
|
Математическая постановка гидродинамической задачи в нулевом приближении (3.9)—(3.12) в пространстве изображений Фурье по переменной х запишется как:
|
|
|
|
|
|
|
|
|
|
|
|
Решение уравнений (4.3), (4.4) с учетом граничных условий (4.5) представляются через ![]() в следующем виде:
в следующем виде:
|
|
|
С помощью выражений (4.6) найдем следы производных из внешних областей:
|
|
|
Подставляя выражения (4.7) в уравнение (4.2), после простых преобразований получим алгебраическое уравнение для определения ![]() :
:
|
|
|
откуда окончательно имеем следующие выражения для решения задачи в пространстве изображений Фурье:
|
|
|
|
|
|
|
|
|
Применяя обратное преобразование Фурье, с использованием соотношения
|
|
|
получим следующие выражения для нулевого приближения:
|
|
|
|
|
|
|
|
|
В справедливости полученных выражений нетрудно убедиться прямой подстановкой выражений в задачу (3.9)—(3.12).
Итак, применение «в среднем точной» модификации асимптотического метода к задаче о фильтрационно-волновом поле в неоднородной анизотропной среде позволяет найти простые аналитические выражения для нулевого коэффициента асимптотического разложения. Это открывает перспективы для решения других задач о фильтрационно-волновых полях в неоднородной пористой среде. Найденные решения описывают поля давления применительно к реальным условиям в акустическом каротаже, сейсморазведке и при интенсификации нефтеизвлечения.
Обозначения
Р — давление, Па (атм.); t — безразмерное время; x, z — линейные координаты; e — параметр асимптотического разложения; w — циклическая частота; с — скорость распространения фильтрационно-волновых возмущений, м/c; k — проницаемость, м2; m — пористость; х, z — декартовы координаты; t — время, с; ![]() — скорость фильтрации, м/c;
— скорость фильтрации, м/c; ![]() — истинная скорость движения жидкости, м/c; β — коэффициент сжимаемости жидкости, Па-1; γ — коэффициент затухания, с-1; μ — вязкость, Па с; ρ — плотность жидкости, кг/м3; ρs — плотность материала скелета, кг/м3; χ — коэффициент пъезопроводности, м2/с.
— истинная скорость движения жидкости, м/c; β — коэффициент сжимаемости жидкости, Па-1; γ — коэффициент затухания, с-1; μ — вязкость, Па с; ρ — плотность жидкости, кг/м3; ρs — плотность материала скелета, кг/м3; χ — коэффициент пъезопроводности, м2/с.
Индексы нижние: 0 — начальные значения параметров; 1 — номер среды; x, z — направление; d (dimension) — размерный.
Индексы верхние (в скобках) — порядковый номер коэффициента асимптотического разложения.
Обозначения математических символов — общепринятые.
Список литературы:
1.Ахметова О.В., Филиппов А.И., Заманова Г.Ф., Поля давления в пласте при пороховом воздействии на слоистую анизотропную среду//Научное Издание. Дифференциальные уравнения и смежные проблемы. Труды международной научной конференции г. Стерлитамак. Отпечатано на множительном участке БГУ 450076, РБ, г. Уфа, ул. Заки Валиди, 32. Том 2. — С. 286. ISBN 978-5-7477-3245-2.
2.Ахметова О.В., Филиппов А.И., Заманова Г.Ф. Асимптотические представления упругих волновых полей в проницаемых пластах. // Акустический журнал, — 2013, — том 59, — № 5, — с. 596—606.
3.Филиппов А.И., Короткова К.Н. Волновые поля давления в пласте и скважине // Физика волновых процессов и радиотехнические системы // Поволжский государственный университет телекоммуникаций и информатики. — 2009. — Т. 12. — № 1. — С. 48—53.
4.Чекалюк Э.Б. Основы пьезометрии залежей нефти и газа. Киев: ГИТЛ УССР. 1965. — 286 с.
5.Zamanova G.F., A.I. Filippov, O.V. Akhmetova. Asymptotic Representations of Elastic Wave Fields in Permeable Strata. // Acoustical Physics, — 2013, — Vol. 59, — № 5 — рр. 548—558
дипломов


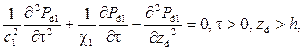
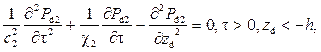
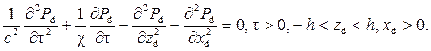

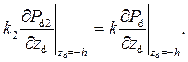
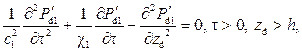
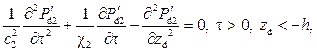
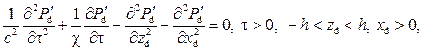
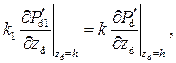
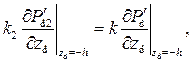
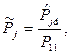
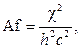
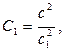

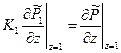 ,
, 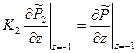 ,
,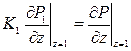 ,
,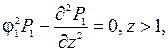

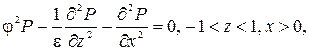
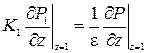 ,
, 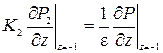 ,
,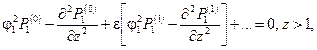
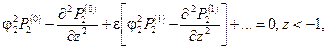


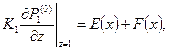
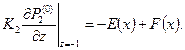
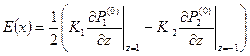
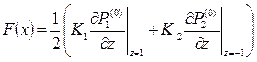
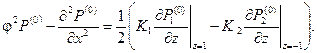
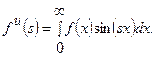
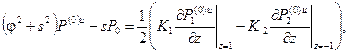
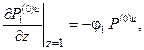
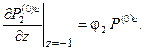
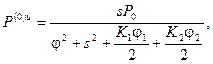
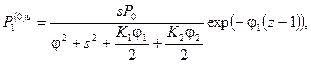
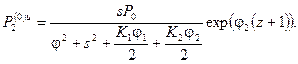
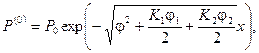
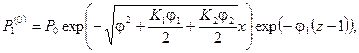

Оставить комментарий