РАСПРЕДЕЛЕНИЕ  ТЕМПЕРАТУРЫ  В  ПРОЦЕССЕ  ЗАМЕРЗАНИЯ  ЖИДКОСТИ  ПРИ  РАЗЛИЧНЫХ  ГРАНИЧНЫХ  И  НАЧАЛЬНЫХ  УСЛОВИЯХ

Калимуллин  Ильдар  Рашитович

студент  5  курса,  факультет  физики  и  математики  БФ  БашГУ,  г.  Бирск

E-mail: 

Балягутдинов  Ильнар  Санирович

студент  5  курса,  факультет  физики  и  математики  БФ  БашГУ,  г.  Бирск

E-mail:  ilnardecyatka@mail.ru

Шагапов  Владислав  Шайхулагзамович

научный  руководитель,  д-р  физ.-мат.  наук,  профессор  БФ  БашГУ,  г.  Бирск

Особый  интерес  представляют  задачи,  в  которых  исследуемое  вещество  испытывает  превращения,  при  которых  оно  переходит  из  одной  фазы  в  другую  с  выделением  или  поглощением  тепла.  Наиболее  распространенными  являются  случаи  плавления  и  затвердевания  (это  задачи  о  промерзании  и  протаивании  влажного  грунта,  об  образовании  льда  на  поверхности  воды,  о  промерзании  трубопроводов,  о  плавлении  и  затвердевании  металла  и  др).  Изменение  физического  состояния  вещества  происходит  при  изменении  температуры  тела,  в  частности,  при  охлаждении  ниже  точки  плавления  происходит  переход  из  жидкой  фазы  в  твердую  [1].

Постановка  задачи  и  основные  уравнения

Рассмотрим  процесс  замерзания  воды,  схема  которого  изображена  на  рис.  1.  Будем  рассматривать  массу  воды,  ограниченную  с  одной  стороны  плоскостью  .  Если  на  поверхности  все  время  поддерживается  постоянная  отрицательная  температура,  то  граница  промерзания    будет  со  временем  проникать  вглубь  жидкости,  образуя  две  области:  область  воды    и  льда  .

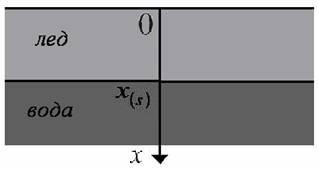
Рисунок  1.  Схема  образования  льда

Обозначим  через    температуру  льда  в  области  ,  а  через    —  температуру  воды  в  области  .  Тогда  задача  об  образовании  льда  может  быть  сформулирована  как  задача  о  сопряжении  двух  температурных  полей  на  движущемся  фронте  промерзания,  то  есть  сведена  к  решению  уравнений  теплопроводности  [6,  4]:

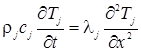,                             (1)

где:  ,  ,  —  плотность,  теплоёмкость,  теплопроводность,    (лед,  вода).

В  начальный  момент  времени    температура  воды  равна

.

На  неподвижной  границе    выполняется  условие  равенства  температур:

.                                     (2)

Так  как  граница    движется  с  неизвестной  заранее  скоростью,  то  на  ней,  кроме  граничного  условия  (2)  для  уравнений  теплопроводности,  должно  быть  задано  ещё  одно  условие,  определяющее  скорость  движения  границы  ,  которое  называется  условием  теплового  баланса:

.                                         (3)

Это  равенство  означает,  что  разность  тепловых  потоков  равна  величине,  которая  тратится  на  образование  льда,  здесь    —  удельная  теплота  замерзания  воды.  Условие  (3)  иногда  называют  условием  Стефана  на  границе  фазового  перехода  [5].

Автомодельное  решение

В  рамках  вышепринятых  уравнений  задача  имеет  автомодельное  решение.  Введем  автомодельную  переменную    и  безразмерные  температуры  ,  ,  . 

В  автомодельных  переменных  уравнения  теплопроводности  (1)  примут  вид:

,

,

где:    —  температуропроводность,    (лед,  вода).

Начальные  и  граничные  условия  запишутся  в  виде:

,

,

.                                    (4)

Тогда  решения  уравнений  теплопроводности  при  заданных  начальных  и  граничных  условиях  будут  иметь  вид:

,  ,                         (5)

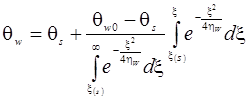,  .              (6)

Подставляя  найденные  решения  в  условие  баланса  тепла  (4),  получаем  трансцендентное  уравнение  для  нахождения  значения  :

,                  (7)

где:  ,  ,  .

В  настоящее  время  имеется  несколько  эффективных  алгоритмов  численного  решения  подобных  уравнений  с  помощью  компьютера,  и  разработано  большое  количество  стандартных  программ  на  различных  языках  программирования.  Эти  алгоритмы  (например,  метод  половинного  деления,  метод  касательных,  метод  хорд  и  др.)  подробно  описаны  в  курсах  численных  методов  анализа.

Результаты  численных  расчетов

На  основе  уравнения  (7)  проведены  численные  расчеты.  Для  параметров,  определяющих  свойства  льда  и  воды,  использованы  следующие  величины  [2,  3]:  ,  ,  ,  ,  ,  ,  . 

На  рис.  2  представлены  распределения  температуры  для  различных  значений  температуры  границы.  Числа  на  кривых  соответствуют  значениям  температуры    в  Кельвинах.

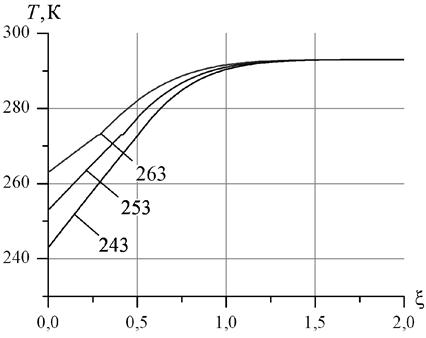
Рисунок  2.  Распределение  температуры  при  значениях  температуры    и  воды  .

При  этом  для  автомодельной  координаты  границы  между  льдом  и  водой  получаются  значения  =0.3,  0.4,  0.5.  Используя  эти  значения  ,  из  формулы  роста  толщины  льда  получаем,  что  за  сутки  может  образоваться  лед  толщиной  =8.8,  12.9,  15.9  см  соответственно.

Данное  автомодельное  решение  позволяет  установить  качественные  закономерности  процесса  образования  льда,  а  также  дать  их  количественную  оценку  при  заданных  граничных  и  начальных  условиях.

Список  литературы:

1.Бобков  В.А.  Производство  и  применение  льда.  М.:  Пищевая  промышленность,  1977.  —  232  с.

2.Варгафтик  Н.Б.  Справочник  по  теплофизическим  свойствам  газов  и  жидкостей.  М.,  1972.  —  720  с.

3.Исаченко  В.П.  и  др.  Теплопередача.  Учебник  для  вузов,  Изд.  3-е,  перераб.  и  доп.  М.,  1975.

4.Карслоу  Г.,  Егер  Д.  Теплопроводность  твердых  тел.  М.:  Наука,  1964.  —  488  с.

5.Кислицин  А.А.  Основы  теплофизики:  Лекции  и  семинары.  Тюмень:  Издательство  Тюменского  государственного  университета,  2002.  —  152  с.

6.Тихонов  А.Н.,  Самарский  А.А.  Уравнения  математической  физики:  Учебник.  7-е  изд.  /  А.Н.  Тихонов,  А.А.  Самарский.  М.:  Изд-во  МГУ;  Изд-во  Наука,  2004.  —  798  с.