ПРОЦЕССЫ САМООРГАНИЗАЦИИ В ПОЛУПРОВОДНИКАХ В СИЛЬНОМ ЭЛЕКТРИЧЕСКОМ ПОЛЕ

Мосичкин Анатолий Федорович

студент 5 курса (магистратура), кафедра теоретической физики ЯрГУ им. П.Г. Демидова, г. Ярославль

E-mail: anatoly_mosichkin@mail.ru

Кузнецов Владимир Степанович

научный руководитель, канд. физ.-мат. наук, доцент, кафедра теоретической физики ЯрГУ им. П.Г. Демидова, г. Ярославль

В настоящее время  полупроводники находят всё большее применение в современном приборостроении. В данной работе исследуются коллективные явления, которые оказываются существенными в области сильных электрических полей ().

На рис. 1 показана схема установки для моделирования токовых неустойчивостей и процессов самоорганизации в полупроводниках [1, с. 5]. Полупроводниковый элемент, состоящий из трёх областей, подключён к источнику постоянного тока: n-область — область, изготовленная из примесного полупроводника n-типа; p-область — область, изготовленная из примесного полупроводника p-типа; i-область — область, состоящая из собственного полупроводника. Будем считать проводимости примесных полупроводников p- и n-типа гораздо больше проводимости собственного полупроводника; это значит, что падение напряжения происходит только в i-области.

Рисунок 1. Схема экспериментальной установки

Поставим задачу об отыскании распределения концентрации носителей заряда в полупроводнике, находящемся в сильном электрическом поле. Для определённости будем рассматривать собственный полупроводник. Как известно, уравнения, которым подчиняются концентрации носителей заряда, имеют вид уравнений непрерывности [3, с. 28]. Запишем уравнения непрерывности для двух типов носителей электрического тока в полупроводнике:

,    (1)

где n — концентрация электронов,

p — концентрация дырок,

e — элементарный заряд,

 — плотность электронного тока,

 — плотность дырочного тока,

f — суммарная скорость тепловой генерации и фотогенерации носителей заряда,

— скорость рекомбинации электронно-дырочной пары,

 — скорость генерации носителей заряда за счёт столкновения с электронами,

 — скорость генерации носителей заряда за счёт столкновения с дырками,

 — суммарная скорость Оже-рекомбинации. Вычитая из первого уравнения системы (1) второе, получим:

                                (2)

Будем рассматривать стационарное распределение электронов и дырок. При этом  и уравнение (2) переходит в:

                                                (3)

Для простоты будем рассматривать одномерную задачу, когда все величины, входящие в уравнение, зависят только от одной переменной (x). Предположим, что полупроводник имеет длину, равную l. Систему координат и направление электрического поля выберем, как показано на рис. 1. В этом случае имеем следующие выражения: n=n(x), p=p(x), , . Причём, как следует из рисунка, , . Используя данные равенства, можно получить следующее выражение: . Тогда. Отсюда следует, что полный электрический ток не зависит от координаты:

                                       (4)

Как известно, плотность электрического тока складывается из плотности полевого и диффузионного токов [3, с. 29]. В таком случае для плотности электронного и дырочного тока можно записать следующие выражения:

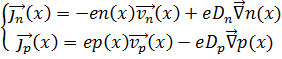,                                (5)

где D_n и D_p — коэффициенты диффузии электронов и дырок соответственно.

В рассматриваемом нами одномерном случае эти уравнения в проекции на ось x примут следующий вид:

.                                     (6)

В сильных электрических полях, очевидно, можно пренебречь диффузионным током по сравнению с полевым. При этом уравнения (6) преобразуются к виду:

.                                                       (7)

Т.к. в сильном электрическом поле наступает явление насыщения, то можно положить v_n(x)=v_p(x)=v=const. Используя данное равенство, складывая уравнения системы (7) с использованием формулы (4), получим:

 .                                                   (8)

Для простоты рассмотрим случай, когда свойства электронов и дырок одинаковы, т. е., когда s₁=s₂=s и β₁=β₂=β. Для краткости будем рассматривать только уравнение на концентрацию дырок в полупроводнике, которое в данном случае принимает вид:

,                    (9)

или, переходя к одномерному случаю, имеем:

.                        (10)

Для удобства дальнейшего анализа этого уравнения перейдём к безразмерным переменным при помощи формул: , . Выражая из данных равенств n и p и подставляя их в уравнение (10), получим:

.              (11)

В процессе введения безразмерных переменных  и  обезразмеривающий параметр n₀ остался неопределённым. Для удобства n₀ можно выбрать так, чтобы выполнялось следующее условие:

.                                                     (12)

Отсюда для n₀ получим:

.                                                       (13)

Вычисления показывают, что n₀=1.57143* 10¹⁶ см^-3.

После всего этого уравнение (11) примет вид: 

.                     (14)

Используя соотношение (7) при условии постоянства скорости движения носителей заряда и деля обе части уравнения (14) на , получим:

.

Для дальнейшего упрощения уравнения можно также обезразмерить и координату с помощью формулы . Подставив x в предыдущее уравнение, приведём его к следующему виду:

.

Для удобства обезразмеривающий параметр x₀ выберем так, чтобы он удовлетворял соотношению:

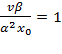.                                                             (15)

Из данного выражения получим:

                                                    (16)

Вычисления показывают, что x₀=57851,2 см. После всех этих манипуляций уравнение на концентрацию дырок в полупроводнике можно представить в виде:

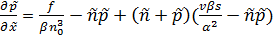.                                  (17)

Представим также и уравнение (8) в обезразмеренном виде:

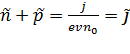.                                                     (18)

Для дальнейшего анализа удобно ввести новую переменную y следующим образом:

.                                                    (19)

При этом видно, что уравнение (18) выполняется автоматически. Подставив данные выражения в уравнение (17) и заменяя частную производную  полной, получим:

.

Поделив обе части уравнения на  и собирая в правой части слагаемые по степеням y, придём к следующему результату:

.                                  (20)

Для краткости константы в уравнении (20) обозначим следующим образом:

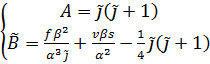.                                          (21)

В таком случае окончательно уравнение (20) приведётся к виду:

                                                  (22)

Из формул (21) видно, что коэффициент  всегда, а коэффициент B может иметь различный знак в зависимости от значения полного тока . Для кремния константы, входящие во все приведённые выражения, имеют следующие числовые значения:; ;  [1, с. 5—6]. Скорость тепловой генерации и фотогенерации носителей заряда можно оценить, используя соотношение: , где  — собственная концентрация свободных носителей () [2]. Подставляя числовые значения, получаем, что . Коэффициенты же ударной ионизации не являются постоянными величинами. Они сильно зависят от напряжённости электрического поля. Эта зависимость описывается следующей аппроксимационной формулой [1, с. 5]:

,                                             (23)

где C_i и b_i — постоянные, определяемые экспериментальным путём, а E — величина электрического поля, приложенного к полупроводниковому образцу. Для электронов и дырок необходимые коэффициенты равны: , , ,  [1, с. 5—6].

С учётом граничных условий на функцию y получаем следующую систему уравнений:

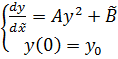.                                          (24)

Данная система будет иметь существенно различные решения в зависимости от знака величины  (рис. 2). Найдём для начала зависимость критического тока  от величины электрического поля E из условия . При этом на величину  получим следующее уравнение:

.                                     (25)

Рисунок 2. Возможные стационарные решения

Домножением на  это уравнение сводится к кубическому относительно , которое имеет вид:

,                                    (26)

где введены следующие обозначения:

.                                              (27)

Вообще говоря, алгебраическое уравнение третьей степени по теореме Безу имеет 3 различных корня. Нас в данном случае интересуют только действительные положительные корни. Проанализируем поведение функции . Для этого исследуем её на экстремум, определив положение максимумов и минимумов:

.                                         (28)

Приравняв производную к нулю и решая полученное квадратное уравнение, получим значение точек экстремума:

Рисунок 3. Примерный вид графика функции F(j)

.                                                           (29)

Отсюда видно, что максимум лежит в отрицательной области, а минимум — в положительной, причём. Из всего этого следует, что график функции  выглядит примерно следующим образом (рис. 3). Получается, что уравнение (26) может иметь либо один положительный вещественный корень и два комплексно-сопряжённых, либо один положительный вещественный корень и два отрицательных. Интересующий нас положительный корень можно выразить аналитически при использовании формул Кардано.

В рассматриваемом случае свойства электронов и дырок считаются одинаковыми, поэтому можно принять, что , . На рис. 4 показан график зависимости  в области сильных электрических полей. Функция  является монотонно возрастающей.

Таким образом, каждому значению электрического поля соответствует определённое значение критического тока:

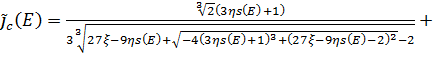
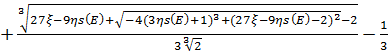
Рисунок 4 . Критический ток

Заранее известно значение электрического поля, приложенного к полупроводниковому образцу, но не тока, протекающего через него, поэтому придётся рассматривать отдельно два случая:  и , которые равносильны случаям  и  соответственно. Решения системы (24) в каждом из этих случаев будут существенно различаться. Это значит, что будет отличаться закон распределения концентрации электронов и дырок в полупроводнике. Теперь найдём закон распределения концентрации носителей заряда, решив систему уравнений (24).

1.                     Случай слабых токов. . В этом случае  . Для удобства введём переобозначение , где . Система (24)  примет вид:

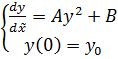                                             (30)

Данная система допускает аналитическое решение, которое выглядит следующим образом:

.                       (31)

Используя данное решение, можно найти вольт-амперную характеристику полупроводникового элемента. Для этого зададим граничные условия, которые имеют вид:

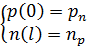,                                                  (32)

где p_n — концентрация дырок в n-области, а n_p — концентрация электронов в p-области. Записывая выражения для удельной проводимости n- и p-областей, получим [2]:

,                                               (33)

где σ_n — удельная проводимость n-области,

σ_p — удельная проводимость p-области,

µ_n — подвижность электронов,

µ_p — подвижность дырок.

Из данных равенств для концентраций n_n и p_p получим следующие выражения:

.                                                     (34)

Считая удельные проводимости n- и p-областей одинаковыми () и используя формулы  и  [2], получим:

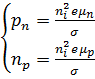.                                                 (35)

Перепишем граничные условия (32) на языке функции . Используя формулы (19), (35), на функцию  можно получить следующее условие:

,                                        (36)

где .

Рисунок 5. Вольт-амперная характеристика в случае слабых токов

В первом приближении подвижности электронов и дырок можно считать одинаковыми, т.е. . Тогда уравнение (36) примет вид:

.                                                (37)

Расписывая это уравнение с использованием выражения (31) и учитывая зависимость коэффициентов A и B от E и , получим неявную функцию, связывающую  и E. График этой функции, построенный в программе Mathematica 6.0, имеет вид, показанный на рис. 5. Используя вольт-амперную характеристику полупроводникового элемента, можно построить график зависимости концентрации носителей заряда от координаты . Возьмём для определённости напряжённость электрического поля E=250 кВ/см. Этому значению соответствует значение критического тока, равное . Подберём параметры полупроводникового элемента так, чтобы ток через него был равен . Это можно сделать путём изменения длины элемента, оставляя при этом постоянным электрическое поле. На рис. 6 показана для этого случая зависимость концентрации электронов и дырок в полупроводнике от координаты . Как видно распределение является периодическим. В данном случае в полупроводнике образуются своеобразные «зоны», состоящие из скоплений электронов и дырок. Т. к. величина  меняется в пределах , то на графиках зависимости  и  имеются области с неизвестным законом распределения концентрации носителей заряда. В остальных же областях эта зависимость описывается аналитически формулами (19) при учёте формулы (31).

2.                     Случай сильных токов. . В этом случае . Для удобства введём переобозначение , где . Система (24) будет выглядеть следующим образом:

Рисунок 6. Концентрация носителей заряда в случае слабых токов

.                                            (38)

Данная система, как и в первом случае, допускает аналитическое решение, которое имеет вид:

.                  (39)

Как и в первом случае из данного решения можно получить вольт-амперную характеристику полупроводникового элемента. Используя граничные условия (32), для отыскания вольт-амперной характеристики, получим снова уравнение (36). Считая подвижности электронов и дырок одинаковыми, перейдём к уравнению (37). Это уравнение, как и в случае 1, определяет неявную функцию, которая связывает  и E. График этой функции, построенный с помощью программы Mathematica 6.0, показан на рис. 7.

Рисунок 7. Вольт-амперная характеристика  в случае сильных токов

Интересно заметить, что вольт-амперные характеристики полупроводникового элемента в обоих случаях практически совпадают. Это связано с тем, что толщина i-слоя l много меньше обезразмеривающего параметра x₀ (). В этом случае , и при разложении в ряд Тейлора выражения (31) и (39) переходят с учётом введённых переобозначений в:

                                      (40)

Таким образом, получаем, что при малой толщине i-слоя, концентрации электронов и дырок линейно меняются вдоль полупроводникового элемента. Нетрудно догадаться, что в случае  функция  может быть как возрастающей, так и убывающей. Это зависит от знака величины : если , то функция  является возрастающей, а если  — убывающей. Построим распределение концентрации носителей заряда в каждом из этих случаев в отдельности:

а) . Изменяя длину полупроводникового элемента при постоянной напряжённости поля (E=250 кВ/см), найдём какое-нибудь значение , при котором данное условие выполняется (). На рис. 8 приведён график зависимости концентрации носителей заряда от координаты в этом случае;

Рисунок 8. Концентрация носителей заряда в случае сильных токов а)

б) . Для реализации данного случая параметр  должен быть достаточно малым (). Качественно график зависимости концентрации электронов и дырок от координаты приведён на рис. 9.

Рис. 9. Концентрация носителей заряда в случае сильных токов б

В случае а), как видно концентрация дырок возрастает вдоль полупроводникового элемента, а концентрация электронов соответственно убывает, как и следовало ожидать. В случае б) имеем обратную ситуацию: концентрация дырок убывает, а концентрация электронов возрастает с координатой вдоль собственного полупроводника.

3. Случай критического тока. . В этом случае . Система (24) примет следующий вид:

                                                 (41)

Решение данной системы выглядит следующим образом:

                                             (42)

График зависимости концентрации носителей заряда от координаты приведён на рис. 10.

Рисунок 10. Концентрация носителей заряда в случае критического тока

Видно, что в данном случае концентрация дырок возрастает с ростом координаты  вдоль собственного полупроводника, а концентрация электронов соответственно убывает. Таким образом, можно сделать вывод о том, что качественно данный случай ничем не отличается от случая 2а). Разница заключается только в количественной зависимости концентрации носителей заряда от координаты.

Рассмотренные четыре случая полностью охватывают все возможные варианты распределения электронов и дырок в полупроводнике при условии, что все коэффициенты, характеризующие свойства электронов и дырок, одинаковы.

Заключение.

В заключении работы подведём основные итоги проведённого исследования процессов самоорганизации в полупроводниках в сильном электрическом поле.

1.  Предложена схема экспериментальной установки для моделирования процессов самоорганизации и токовых неустойчивостей в полупроводниках в сильном электрическом поле.

2.  Предложена математическая модель процессов самоорганизации в полупроводниках в сильном электрическом поле.

3.  Найдены возможные стационарные распределения концентрации носителей заряда в собственном полупроводнике в области электрических полей, близких к пробивному.

4.  Получена зависимость критического тока от величины электрического поля для кремниевого полупроводника.

5.  Теоретически рассчитаны вольт-амперные характеристики полупроводникового лавинного диода для случая слабых и сильных токов, которые оказались практически совпадающими.

6.  Проведён теоретический анализ возможных распределений концентрации носителей заряда в собственном полупроводнике.

Список литературы:

1.Кузнецов В.С., Кузнецов П.А. Пространственная самоорганизация свободных носителей тока в электрических полях // Научный журнал «Вестник ЯрГУ. Серия Естественные и технические науки». Ярославль, 2011. № 2.

2.Манаев Е.И. Основы радиоэлектроники: учеб. пособие для вузов. М.: Радио и связь, 1985.

3.Шёлль Э. Самоорганизация в полупроводниках. М.: Мир, 1991.