О РАВНОВЕСИИ ИНТЕРВАЛЬНОЙ МОДЕЛИ ЛЕОНТЬЕВА ПРИ ОГРАНИЧЕНИЯХ НА ВЕКТОРЫ ИНТЕНСИВНОСТЕЙ ПРОИЗВОДСТВА

О РАВНОВЕСИИ ИНТЕРВАЛЬНОЙ МОДЕЛИ ЛЕОНТЬЕВА ПРИ ОГРАНИЧЕНИЯХ НА ВЕКТОРЫ ИНТЕНСИВНОСТЕЙ ПРОИЗВОДСТВА

Козловская Яна Игоревна

магистрант 2 курса, кафедра прикладной математики, ПНИПУ, РФ, г. Пермь

E-mail:

Севодин Михаил Алексеевич

научный руководитель, к.ф.-м.н., доцент кафедры прикладной математики, ПНИПУ, РФ, г. Пермь

В экономике часто возникает задача нахождения равновесного состояния экономики ([1]-[4], [6]). При этом главным вопросом считается нахождение параметров экономической системы, соответствующих этому равновесному положению. Наряду с этим необходимо иметь в виду, что возможны ограничения на технологические множества, задающие интенсивности производственных отраслей [7], [8].

В данной работе исследуется случай, при котором ограничения на технологическое множество заданы в виде выпуклого конуса. Так как векторы цен и векторы интенсивностей модели взаимосвязаны, из ограничений вектора интенсивностей вытекает ограничение вектора цен. При этом векторы цен ограничиваются конусом, в некотором смысле симметричным к конусу, ограничивающему интенсивности производства. В более ранних работах [7], [8] этот факт не рассматривался. Кроме того, в работе дается оценка положения равновесия модели при условии, что производственная матрица задается с помощью интервальных чисел [5]. Такая оценка получается с помощью перехода  к оптимизационным задачам.

Модель Леонтьева определяется матрицей  [2], [7]. Пусть  - неразложима и примитивна. Пусть  - вектор интенсивностей,  - вектор цен. Тогда динамическое равновесие модели задается соотношениями [2]:

 .                               (1)

Здесь - единичная матрица,  - положительное число.

Предположим, что вектор  принадлежат не всему  [6], а выпуклому многогранному конусу  с матрицей  [4], т.е. .  Причем , и матрицы  и  коммутативны. Пусть  имеет обратную матрицу . Обозначим через  конус, причем . Имеет место

Теорема 1. Пусть в неотрицательной матрице  нет нулевых строк. Тогда существует решение системы (1) .

Доказательство. Опишем подробно переход от неравенства ,  к неравенству ,  [2].

Обозначим . Тогда неравенства

                                                              (2)

при подстановке  равносильны неравенствам:

Поэтому

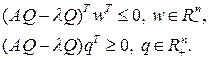
Таким образом, неравенства (2) эквивалентны неравенствам

.                                                                (3)

Система (3) соответствует модели Неймана , и, значит [2], имеет решение. Так как (3) эквивалентна (2), то и (2) имеет решение. Справедливость третьего соотношения в (1) устанавливается аналогично. Теорема доказана.

Общим положением равновесия модели Леонтьева с производственной матрицей  и матрицей ограничений  назовем решение  системы (2) , соответствующее решению системы (1).

Частные положения равновесия с соответствующими экстремальными значениями  можно найти, перейдя к оптимизационным задачам [1]:

                                   (4)

                              (5)

Числа  и  называются числами Неймана и Фробениуса и определяют максимальный и минимальный темп равновесного роста модели соответственно.

Заметим, что все элементы матрицы  неотрицательны (). Из однородности задачи следует, что можно ограничиться случаем, когда векторы  и  принадлежат симплексам. При введении в систему матрицы  однородность сохраняется, поэтому по-прежнему можно считать, что ,  и , . Здесь .

Тогда из (4) и (5) следует, что для нахождения набора параметров продуктивности  модели и ее положения равновесия следует решить оптимизационную задачу вида [5]:

                                                       (6)

      (7)

В этом случае можно получить оценки положения равновесия моделей при интервальном описании матрицы .

Интервальной назовем модель Леонтьева (2) с матрицей затрат . Здесь  – матрица центров интервалов матрицы;  - матрицы точных верхних и нижних граней соответственно [5].

Теорема 2. Если в модели Леонтьева с интервальной матрицей  и ограничением в виде выпуклого конуса с матрицей , матрица  принадлежит классу средних матриц с , и точечная матрица  удовлетворяет условию ,  то .

Доказательство. Из (6) и (7) при замене  следует, что для нахождения параметров равновесия модели с точечной матрицей  следует решить задачу:

                                    Используем условие . Тогда:

.    (8)

Задача (8) позволяет найти параметры равновесия точечной модели с матрицей . Учитывая замену переменных, делаем вывод, что набор  определяет положение равновесия модели с матрицей .

Теорема 2 показывает, что если неопределенность матрицы  состоит в незнании , то  можно найти с использованием матрицы центров интервалов.

Теорема 3. Пусть модель Леонтьева задана интервальной матрицей  и ограничением в виде выпуклого конуса с матрицей . Пусть также для точечной матрицы  выполнены условия: _,

_{,                                                                                                           (9)}

_{,                                                                                                         (10)}

_{.                                                                                                          (11)}

Тогда .

Доказательство аналогично [5] и основывается на заменах  и подстановке их в (9), а также использовании условий (10) и (11).

Список литературы:

1.  Альсевич В. В. Введение в математическую экономику. Конструктивная теория. / Альсевич В. В. – М.: Едиториал УРСС, 2005. - 256 с.

2.  Ашманов С. А. Математические модели и методы в экономике / Ашманов С.А. –  М. ОНИКС, 2012. – 199 с. 

3.  Макаров В. Л. Математическая теория экономической динамики и равновесия / Макаров В. Л., Рубинов А. М. –   М.: Наука, 1973.–335 с.

4.  Никайдо Х. Выпуклые структуры и математическая экономика / Никайдо Х. – М.: Мир, 1972. 519 с.

5.  Панюков А. В., Латипова А. Т. Оценка положения равновесия в модели Неймана при интервальной неопределенности исходных данных//Вестник УГАТУ.-2008, - т.10, №2(27), - С. 150-153.

6.  Рубинов А. М. Экономическая динамика // Итоги науки и техники. Серия «Современные проблемы математики» М., 1982. № 19. –  с. 59–110.

7.  Севодин М. А. Динамические системы леонтьевского типа с ограничениями на интенсивности технологических процессов // Наука и бизнес: пути развития.- 2013,- № 8, - С. 66-70.

8.  Севодин М. А. Модель Неймана с ограничениями пропорций роста интенсивностей производственных процессов // Современные проблемы науки и образования.-2013,-№6. Режим доступа: http://www.science-education.ru/pdf/2014/1/268.pdf