Статья опубликована в рамках: XXVII Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ЭКОНОМИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 18 декабря 2014 г.)
Наука: Экономика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ЭКОНОМИКЕ
Иванцова Ирина Арсентьевна
студент 2 курса, кафедра экономики, филиала РУДН, РФ, г. Сочи
Кошевая Наталья Сергеевна
научный руководитель, ст. преподаватель кафедра экономики, филиала РУДН, РФ, г. Сочи
В жизни общества одно из важнейших мест занимает экономическая сфера, то есть все то, что связано с производством, распределением, обменом и потреблением созданных трудом человека благ.
Под экономикой принято понимать систему общественного производства, процесс создания материальных благ, необходимых человеческому обществу для его нормального существования и развития, а также науку, изучающую экономические процессы.
Экономика играет огромную роль в жизни общества. Она обеспечивает людей материальными условиями существования: продуктами питания, одеждой, жильем и иными предметами потребления.
Экономическая сфера — главная сфера жизни общества, она определяет ход всех происходящих в нем процессов.
Глубокие и стремительные экономические изменения в современном мире обусловливают необходимость поиска новых подходов к анализу экономической жизни общества, исследованию особенностей и перспектив национальной экономики, основу которой составляют предприятия, фирмы, организации, домашние хозяйства, объединенные экономическими взаимоотношениями в единое целое, выполняющие определенные функции в общественном разделении труда, производящие товары или услуги.
Череда кризисов, переживаемых европейской и мировой экономикой, также коснулась и России, перед которой теперь стоит немало экономических проблем. Поэтому важную роль в изменении этой ситуации сыграет высшее образование, которое готовит выпускников экономических специальностей к работе в новых условиях. Именно они должны выступить как своего рода новаторами экономического мышления и поведения в нашей стране.
Российская система образования, на наш взгляд, должна обеспечивать экономику страны квалифицированными кадрами, которые умеют решать профессиональные задачи на основе высокой математической культуре.
В настоящее время наибольших успехов достигают те отрасли науки, которые широко используют математический аппарат в своих исследованиях.
Современная экономическая теория включает в себя такой элемент как математические модели и методы. Использование математики в экономике позволяет выделять и анализировать важные связи экономических переменных и объектов.
В математике существует больше инструментов для описания детерминированных (определённых) связей, которые в экономике распространены менее чем стохастические (статистические). Детерминированные связи наиболее часто встречаются на микроуровне экономики: межотраслевой баланс, модели экономического роста. На макро уровне в основном стохастические связи: теория вероятностей, теория игр, многомерный статистический анализ.
В данной статье нам бы хотелось разобрать некоторые задачи финансовой математики с помощью понятий - ковариация и коэффициент корреляции.
Ковариация – числовая характеристика совместного распределения двух случайных величин, которая равна математическому ожиданию произведения отклонений случайных величин от их математических ожиданий.
Ковариация определяется для случайных величин X и Y с конечными дисперсиями и обозначаются cov (X,Y).
Таким образом, ковариация определяется формулой:
![]()
где: Xi и Yi — i-е значения соответствующих дискретных случайных величин X и Y,
M (X) — математическое ожидание ДСВ X,
M (Y) — математическое ожидание ДСВ Y, i =1,2…n.
При этом cov (X,Y) = cov (Y,X); cov (X,X) = D(X). Если величины X и Y независимы, то cov (X,Y)=0.
Так как ковариация связана непосредственно с понятиями математическое ожидание и стандартное отклонение, то напомним их определение.
Математическим ожиданием M(X) дискретной случайной величины X называется сумма произведений всех её значений на соответствующие им вероятности.
![]()
Стандартным отклонением ![]() случайной величины X называется арифметическое значение корня квадратного из её дисперсии.
случайной величины X называется арифметическое значение корня квадратного из её дисперсии.
![]()
Дисперсией D(X) случайной величины X называется математическое ожидание квадрата её отклонения от математического ожидания.
![]()
Рассматривая, любую финансовую, кредитную коммерческую операцию нужно предполагать совокупность условий, согласованных её участниками.
К таким условиям относятся: сумма кредита, займа, инвестиций, цена товара, сроки, способы начисления процентов, погашения долга. Совместное влияние на финансовую операцию многих факторов делает её конечный результат неочевидным; для его оценивания необходим специальный количественный анализ.
Совокупность методов этого анализа и составляет предмет финансовой математики. Именно размер платежа, срок и ставка процента составляют основу количественного финансового анализа, целью которого является решения широкого круга задач: от элементарного начисления процентов до анализа сложных кредитных и коммерческих операций.
Рассмотрим одну из финансовых задач.
Нам предстоит сделать одну из двух альтернативных инвестиций.
Пример 1.
Первая инвестиция представляет собой вложение средств во взаимный фонд, владеющий различными акциями, определяющими индекс Тодоса. Назовём его фондом Тодоса.
Вторая инвестиция — это приобретение акций взаимного фонда, приносящих наибольшую доходность во время экономического спада. Присвоим ему название фонд экономического спада.
Оценить доходность каждой инвестиции (прибыль на 1000 долларов) для каждого из трёх возможных вариантов состояния экономики, имеющих определенную вероятность.
Прогнозируемая прибыль от каждой инвестиции для каждого из трёх возможных вариантов состояния экономики приведены в таблице № 1
Таблица 1.
Таблица прогнозирования прибыли от каждой инвестиции
|
Инвестиции |
|||
|
P(X,Y) |
Состояние экономики |
Фонд Тодоса
долл. |
Фонд экономического спада долл. |
|
0,2 |
экономический спад |
-100 |
250 |
|
0,5 |
стабильная экономика |
100 |
50 |
|
0,3 |
экономический рост |
300 |
-100 |
Математическое ожидание и стандартное отклонение доходности каждой инвестиции, а также ковариация между их показателями доходности вычисляются следующим образом.
Обозначим X — доходность фонда Тодоса, Y — доходность фонда экономического спада.
Имеем:
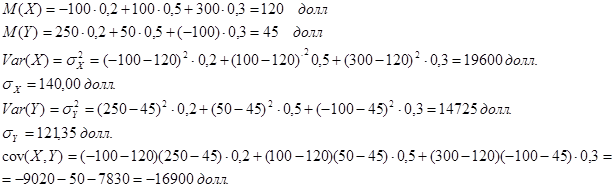
Таким образом, математическое ожидание доходности фонда Тодоса выше, чем у фонда экономического спада.
Однако стандартное отклонение фонда Тодоса также превышает стандартное отклонение фонда экономического спада, что говорит о более высокой степени риска.
Ковариация между показателями доходности обоих фондов обратно пропорциональна, если доходность одного из фондов возрастает, то доходность другого снижается.
Рассмотрим другое применение математического ожидания и стандартного отклонения двух случайных величин, которые позволяют оценить доходность и риск портфельных инвестиций.
Диверсифицируя свои вклады, инвесторы приобретают разные ценные бумаги, стремясь получить максимум прибыли при минимальном риске. При исследовании доходности портфелей ценных бумаг каждому пакету акций присваивают определенный вес. Это позволяет оценить ожидаемую доходность портфеля акций и его риск.
Ожидаемая доходность портфеля ценных бумаг , состоящего из двух пакетов акций:
Е(Р) = wE(X) + (1 – w)E(Y)![]()
где: Е(Р) — ожидаемая доходность портфеля,
Е(Х) — ожидаемая доходность пакета акций X (где E(P)=M(X)),
E(Y) — ожидаемая доходность пакета акций Y ( E(Y)=M(Y)),
W — доля пакета акций X в портфеле ценных бумаг,
(1 – w) — доля пакета акций Y в портфеле ценных бумаг.
Риск портфеля ценных бумаг:
![]()
В предыдущем примере мы оценили математическое ожидание и стандартное отклонение инвестиций в фонд Тодоса и фонд экономического спада, а также ковариацию между ними.
Пример 2.
Допустим, что портфель активов состоит из пакетов акций двух фондов стоимостью по 800 долл. каждый. Вычислим ожидаемую доходность и риск такого портфеля акций, используя формулы (5) и (6):
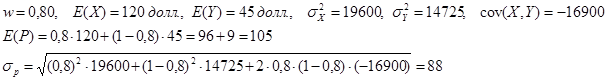
Таким образом, ожидаемая доходность портфеля составляет 105 долл. на каждую тысячу вложенных долларов, а риск портфельных инвестиций равен 88 долл. Так как инвестиции приносят максимальную прибыль в разных экономических ситуациях, то это позволяет минимизировать общий риск.
Рассмотрим теперь понятие коэффициент корреляции и его применение.
Корреляция — это статистическая зависимость двух и более независимых друг от друга величин. При этом изменение значения одной их них приводит к изменению значения других. В качестве математической меры корреляции двух величин служит коэффициент корреляции.
Коэффициенты корреляции могут быть как положительными, так и отрицательными:
· если при увеличении значения одной величины происходит уменьшение значения другой величины, то их коэффициент корреляции отрицательный;
· если при увеличении значения одной величины влечёт за собой увеличение значения другой величины, то в этом случае можно говорить о положительном коэффициенте корреляции.
В том случае, когда между величинами отсутствует статистическая взаимосвязь, то говорят, что случайные величины независимы.
Коэффициент корреляции K демонстрирует нам, насколько ярко выражена тенденция роста одной переменной при увеличении другой. Его значения всегда находятся в промежутке [-1; 1]. Чем ближе значение переменной к -1 или 1, тем сильнее взаимосвязь между исследуемыми величинами. Если коэффициент корреляции равен нулю (K=0), то можно говорить о полном отсутствии связи между величинами, если же он равен одному (K=1) или минус одному (K= -1), то говорят о функциональной зависимости величин.
Рассмотрим пример с применением линейной корреляции.
Пример3. По данным о стоимости основных производственных фондов и объёме валовой продукции предприятий необходимо оценить тесноту связи признаков.
Рассмотрим тесноту связей признаков с помощью линейного коэффициента корреляции ![]() .
.
Степень тесноты связи признаков определяется с помощью шкалы Чеддока приведённая в таблице № 2:
Таблица 2.
Шкала Чеддока
|
|
0,1-0,3 |
0,3-0,5 |
0,5-0,7 |
0,7-0,9 |
0,9-1,0 |
|
степень связи |
слабая |
умеренная |
заметная |
высокая |
тесная |
Расчёт линейного коэффициента корреляции производится по следующим формулам:
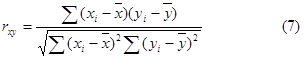
или

где: xi , yi — i-е значения факторного и результативного признаков;
![]() — средние значения признаков;
— средние значения признаков;
![]() — средняя произведений индивидуальных значений признаков;
— средняя произведений индивидуальных значений признаков;
Sx , Sy — выборочные средние квадратические отклонения признаков.
Для определения взаимосвязи основных производственных фондов и объёмом валовой продукции предприятий составим таблицу № 3:
Таблица 3.
Таблица взаимосвязи основных производственных фондов и объёмов валовой продукции
|
Номер предприятия |
Стоимость основных производственных фондов, млн. руб. xi |
Объём валовой продукции млн. руб. yi |
xi yi |
xi2 |
yi2 |
|
1 |
1 |
20 |
20 |
1 |
400 |
|
2 |
2 |
25 |
50 |
4 |
625 |
|
3 |
3 |
31 |
93 |
9 |
961 |
|
4 |
4 |
31 |
124 |
14 |
961 |
|
5 |
5 |
40 |
200 |
25 |
1600 |
|
6 |
6 |
56 |
336 |
36 |
3136 |
|
7 |
7 |
52 |
364 |
49 |
2704 |
|
8 |
8 |
60 |
480 |
64 |
3600 |
|
9 |
9 |
60 |
540 |
81 |
3600 |
|
10 |
10 |
70 |
700 |
100 |
4900 |
|
S |
55 |
445 |
2907 |
385 |
22487 |
С помощью таблицы 3 рассчитаем линейную корреляцию:
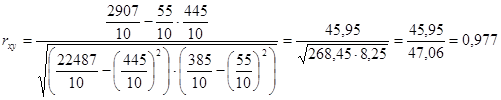
Коэффициент линейной корреляции близок к единице, следовательно, связь исследуемых признаков тесная.
Как видим, математика и экономика дополняют друг друга. Так математические модели помогают экономистам найти оптимальные способы принятия управленческих решений, а экономика ставит перед математикой всё новые задачи и стимулирует поиск методов их решения.
Список литературы:
1.Красс М.С. Математика в экономике: математические методы и модели учебник для бакалавров. 2-е изд. испр. и доп., 2013.
2.Кремер Н.Ш. Теория вероятностей и математическая статистика учебник 3-е изд. М. 2010.
3.Левин Д.М. и др. Статистика для менеджеров. М: Вильямс, 2004 — с. 300—303.
дипломов


Оставить комментарий