АНАЛИЗ  И  ПРОГНОЗИРОВАНИЕ  НА  ОСНОВЕ  КОРОТКИХ  ВРЕМЕННЫХ  РЯДОВ

Ефремова  Елена  Алексеевна

студент  5  курса,  кафедры  ММиМЭ,  ОГУ,  РФ,  г.  Оренбург

E-mail: 

Прядкина  Вера  Алексеевна

студент  5  курса,  кафедры  ММиМЭ,  ОГУ,  РФ,  г.  Оренбург

E-mail: 

В  настоящее  время  производственно-экономические  отношения  являются  довольно  изменчивыми.  В  свою  очередь  законодательная  база,  регулирующая  эти  отношения,  оказывается  неустойчивой  и  неполной.  Все  это  приводит  к  тому,  что  временные  ряды,  характеризующие  многие  производственные,  экономические  и  социально-экономические  процессы,  имеют  мало  уровней  (значений).  Кроме  того,  стоит  отметить,  что  постоянно  происходит  появление  многих  новых  процессов  в  производственной  и  социальной  сферах.  В  связи  с  тем,  что  данные  процессы  ранее  не  являлись  предметом  статистического  учета,  они  представляются  физически  короткими  временными  рядами.

При  исследовании  и  прогнозировании  коротких  временных  рядов  возникает  проблема  неполноты  и  неточности  исходной  информации,  которая  связана:  во-первых,  со  сложностями,  возникающими  при  сборе  и  учете  информации  об  исследуемом  процессе  или  явлении;  во-вторых,  с  отсутствием  достоверности  и  полноты  исходных  данных  о  прогнозируемом  процессе;  в-третьих,  с  возникновением  особенностей,  существование  которых  ранее  не  предполагалось,  в-четвертых,  прогноз,  обладающий  высокой  точностью,  можно  получить  лишь  когда  временные  ряды  содержат  не  менее  50  уровней,  в-пятых,  в  связи  с  нестационарностью  коротких  временных  рядов  невозможно  применение  хорошо  разработанных  и  изученных  методов,  моделей  и  алгоритмов  прогнозирования  [2].

Наиболее  часто  используемые  подходы  прогнозирования  достаточно  полно  изложены  в  научных  трудах  Айвазяна  С.А,  Бокса  Дж.,  Дженкинса  Г.  и  др.  Различные  методы  прогнозирования  широко  представлены  в  таких  пакетах  программ,  как  SPSS,  STADIA,  STATISTICA,  GRETL  и  др.  Однако  ни  в  работах  данных  авторов,  ни  в  методах,  реализованных  в  программных  пакетах,  не  подразумевается  прогнозирование  процессов,  представленных  малым  объемом  статистического  материала.

Таким  образом,  существует  необходимость  в  исследовании  новых  альтернативных  подходов  прогнозирования  коротких  временных  рядов  и  корректировке  уже  существующих  подходов.

Всем  вышеизложенным  обосновывается  актуальность  темы  исследования.

Для  исследования  будем  использовать  данные  доходов  предприятия  ООО  «Аллфомит»  с  момента  его  функционирования  на  рынке  —  август  2013  года,  по  июнь  2014  года.  Предприятие  занимается  продажей,  ремонтом  и  обслуживанием  промышленного  пищевого  оборудования.

Среди  новых  направлений,  применяемых  для  исследования  и  прогнозирования  коротких  временных  рядов,  можно  выделить  методы  и  модели  искусственного  интеллекта,  в  частности  нейросетевые  модели.

Осуществим  прогнозирование  в  ППП  STATISTICA  8.0.  В  результате  обучения  было  построено  5  сетей  (рисунок  1). 

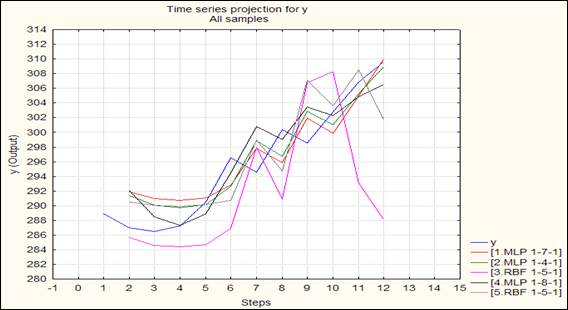
Рисунок  1.  Динамика  доходов  ООО  «Аллфомит»  в  период  август  2013  г.  —  июнь  2014  г.  и  модельных  значений  на  август-октябрь  2014  г.,  тыс.  руб.

Для  прогнозирования  была  использована  сеть  «Многослойный  персептрон»  с  наименьшей  ошибкой  для  сети  [1].  На  рисунке  2  представлен  прогноз  на  3  периода  вперед,  построенный  на  основе  аппарата  нейронных  сетей.

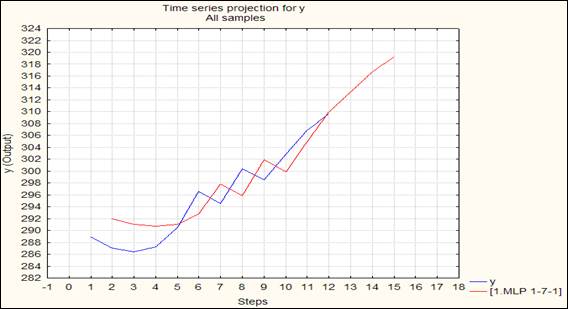
Рисунок  2.  Динамика  доходов  ООО  «Аллфомит»  в  период  август  2013  г.  —  июнь  2014  г.  и  прогнозные  значения  по  сети  на  август-октябрь  2014  г.,  тыс.  руб.

Таким  образом,  можно  сделать  вывод,  что  прогноз  обладает  высокой  точностью,  так  как  ошибка  аппроксимации  меньше  10  %  и  составляет  2,458  %. 

Поскольку  основной  задачей  социально-экономического  прогнозирования  является  построение  прогнозных  моделей,  наилучшим  способом  описывающих  динамику  развития,  то  при  прогнозировании  таких  процессов  используют  адаптивные  методы.  Адаптивные  методы  позволяют  в  большей  степени  учитывать  текущую  информацию  и  в  меньшей  степени  —  прошлую.  Основное  свойство  таких  методов  заключается  в  изменении  коэффициентов  построенной  модели  при  поступлении  новой  информации,  то  есть  адаптация  моделей  к  новым  данным.  Одним  из  таких  методов  является  адаптивный  метод  Брауна  [2].

Модель  Брауна  для  малых  выборок  в  полной  форме  с  учетом  начальных  значений  имеет  вид  [2]:

,  (1)

при 

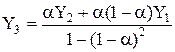,  (2)

где  .

Рассмотрим  возможность  применения  данного  подхода  к  краткосрочному  прогнозированию  временного  ряда.  Экспоненциально  взвешенные  значения  коэффициента  пропорциональности  по  методу  Брауна: 

  .  (3)

Прогноз  показателя    на  следующий  шаг  наблюдения    выполняется  так:

.  (4)

Помимо  простоты  вычисления,  важно,  что  оптимизации  подвергается  только  один  параметр    [2].

Оптимальные  значения  постоянной  сглаживания  находится  их  условия  минимума  дисперсии  ошибки  аппроксимации:

  (5)

Таким  образом,  на  рисунке  3  представлен  прогноз,  построенный  по  методу  Брауна  для  коротких  выборок,  на  3  периода  вперед.

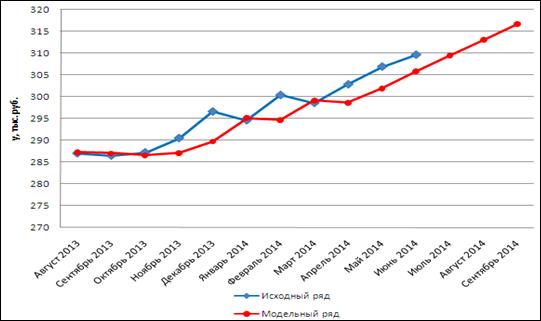
Рисунок  3.  Динамика  доходов  ООО  «Аллфомит»  в  период  август  2013  г.  —  июнь  2014  г.  и  прогнозные  значения  по  методу  Брауна  при    на  август-октябрь  2014  г.,  тыс.  руб.

Прогноз  обладает  высокой  точностью,  так  как  ошибка  аппроксимации  меньше  10  %  и  составляет  1,36  %.

Перейдем  к  прогнозированию  методом  SSA  (Singular  Spectrum  Analysis  или  «Гусеница»),  который  является  мощным  средством  исследования  временных  рядов.  Суть  метода  состоит  в  преобразовании  одномерного  ряда  в  многомерный  с  помощью  однопараметрической  сдвиговой  процедуры  (отсюда  и  название  «Гусеница»).  Далее  проводится  исследование  полученной  многомерной  траектории.  Для  этого  проводится  анализ  главных  компонент  (сингулярное  разложение).  На  завершающем  этапе  осуществляется  восстановление  (аппроксимация)  ряда  по  выбранным  главным  компонентам  [3]. 

После  применения  данного  метода  временной  ряд  раскладывается  на  простые  компоненты,  такие  как  тренды,  сезонные,  периодические  или  колебательные  составляющие,  а  также  шумовые  компоненты. 

Наиболее  успешно  метод  SSA  применяют  в  геофизике,  гидрологии,  метеорологии,  климатологии,  а  также  в  экономике,  т.  е.  там,  где  возникает  необходимость  в  исследовании  различных  временных  рядов:  коротких  и  длинных,  одномерных  и  многомерных  стационарных  и  нестационарных  [4]. 

Таким  образом,  на  рисунке  4  представлен  прогноз,  построенный  по  методу  SSA  на  3  периода  вперед  в  программе  Caterpillar  2.00.

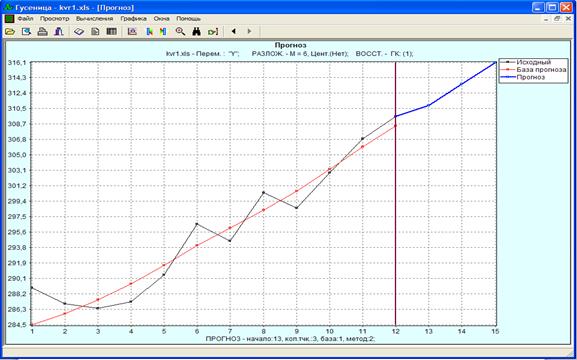
Рисунок  4.  Динамика  доходов  ООО  «Аллфомит»  в  период  август  2013  г.  —  июнь  2014  г.  и  прогнозные  значения  по  методу  SSA   на  август-октябрь  2014  г.,  тыс.  руб.

Таким  образом,  прогноз  обладает  высокой  точностью,  так  как  ошибка  аппроксимации  меньше  10  %  и  составляет  1,501  %. 

Расчитаем  критерий  Акаике,  модифицированный  для  коротких  временных  рядов.

,  (6)

где  .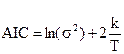

Таблица  1. 

Значения  модифицированного  критерия  Акаике

По  таблице  1  можно  сделать  вывод,  что  наилучший  прогноз  получен  с  помощью  метода  SSA  («Гусеница»). 

Таким  образом,  проведен  анализ  методов,  пригодных  для  моделирования  и  прогнозирования  коротких  временных  рядов.  К  ним  относятся  модели,  основанные  на  нейронных  сетях,  метод  Брауна,  адаптированный  для  коротких  временных  рядов,  и  метод  SSA.  Данные  методы  показали  хорошие  результаты  и  высокую  точность  прогноза.  Также  рассмотрен  критерий  Акаике,  модифицированный  для  коротких  временных  рядов,  на  основе  которого  было  установлено,  что  наилучшим  оказался  метод  SSA.

Список   литературы:

1.Боровиков  В.П.  Нейронные  сети.  STATISTICA  Neural  Networks:  Методология  и  технологии  современного  анализа  данных  /  Под  редакцией  В.П.  Боровикова.  2-е  изд.,  перераб.  и  доп.  М.:  Горячая  линия  Телеком,  2008.  —  392  с.  ISBN:  978-5-9912-0015-8.

2.Светуньков  С.Г.  Методы  социально-экономического  прогнозирования:  учебник  для  вузов.  Том  II  /  С.Г.  Светуньков,  И.С.  Светуньков.  СПб.:  Изд-во  СПбГУЭФ,  2010.  —  103  с.  ISBN:  978-5-7310-2476.

3.Golyandina  N.,  Nekrutkin  V.,  Zhigljavsky  A.А.  Analysis  of  Time  Series  Structure:  SSA  and  Related  Techniques  //  Chapman  &  Hall/CRC  Monographs  on  Statistics  &  Applied  Probability.  2001.  —  320  p.

4.            Golyandina  N.,  Zhigljavsky  A.А.  Singular  Spectrum  Analysis  for  Time  Series.  2013,  IX,  —  120  p.  ISBN:  978-3-642-34912-6.