Статья опубликована в рамках: XV Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ЭКОНОМИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 26 декабря 2013 г.)
Наука: Экономика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ВОПРОСЫ ИССЛЕДОВАНИЯ ВАРИАНТОВ ТЕХНИЧЕСКИХ РЕШЕНИЙ В УСЛОВИЯХ НЕОДНОЗНАЧНОСТИ ИНФОРМАЦИИ
Карташов Роман Сергеевич
студент 4 курса, кафедра «Автоматизированные электротехнологические
установки и системы» СГТУ имени Гагарина Ю.А., РФ, г. Саратов
E-mail:
Пименов Арсений Николаевич
студент 4 курса, кафедра «Автоматизированные электротехнологические установки и системы» СГТУ имени Гагарина Ю.А., РФ, г. Саратов
E-mail:
Гусева Наталия Васильевна
научный руководитель, канд. экон. наук, доцент СГТУ имени Гагарина Ю.А., РФ, г. Саратов
Системы энергетики – объекты сложные. В ряде случаев решение о выборе оптимального варианта их развития не может быть сделано на основе какого-либо одного экономического критерия: затрат, прибыли, рентабельности или чистого дисконтированного дохода.
Очень часто приходится принимать решение с учетом достижения различных, иногда даже противоречивых, целей. Так, например, наряду с минимумом затрат стараются обеспечить максимум надежности электроснабжения, минимум расхода цветного металла и максимум производительности труда [1, 2].
Критерии достижения частных (локальных) целей:
![]() ,
,
где: j — индекс локального критерия,
n — число критериев,
образуют вектор критериев ![]() .
.
Поэтому такого рода задачи называют задачами векторной оптимизации или многокритериальными задачами.
Решение многокритериальных задач лежит в области компромисса, так как с точки зрения математики достижение экстремальных значений n-функциями лишено смысла.
Главная проблема решения таких задач — выбор принципа оптимальности.
В статье рассмотрен вопрос решения этой проблемы на примере выбора наиболее экономичного варианта схемы районной электрической сети из шести возможных стратегий.
В таблице 1 представлены показатели схем электроснабжения по вариантам.
Таблица 1.
Матрица локальных критериев
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Критерии достижения целей имеют разные единицы измерения, поэтому необходимо провести нормирование частных критериев по формулам:
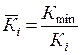 , (1)
, (1)
 , (2)
, (2)
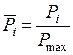 , (3)
, (3)
где: Кmin — минимальные капитальные вложения из ряда стратегий, млн. руб.;
Кi — капитальные вложения i-й стратегии, млн. руб.;
ΔPmin — минимальные потери мощности из ряда стратегий, МВт;
ΔPi — потери мощности i-й стратегии, МВт;
Pmax — наибольшая передаваемая мощность, МВт;
Pi — передаваемая мощность i-й стратегии, МВт.
Результаты нормирования сведены в таблицу 2.
Таблица 2.
Матрица нормированных критериев
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для комплексной оценки эффективности вариантов 1÷6 необходимо установление некоторой схемы компромисса — принципа согласования оптимумов по разным критериям.
Число возможных схем компромисса очень велико, но во всех случаях его задача — это сведение векторной задачи оптимизации к эквивалентной (в смысле принятого принципа оптимальности) скалярной (т. е. однокритериальной) задаче.
Различные схемы компромисса, в первую очередь, могут отличаться по наличию или отсутствию приоритетов в достижении локальных целей.
В том случае, когда достижение отдельных целей предпочтительнее достижения других, то для оценки степени предпочтительности вводятся приоритеты. Приоритет локальных критериев может задаваться различными способами. Наибольшее распространение получил способ, который состоит в задании весовых коэффициентов для каждого локального критерия — ![]() .
.
Следовательно, каждому критерию (цели) по степени важности присваивается весовой коэффициент, соответственно:
![]() ,
,
![]() ,
,
![]() .
.
Производится оценка важности каждой цели определенным числом аj так, чтобы для более важной цели аj было больше, чем для менее важной:
![]() , (4)
, (4)
Так как ![]() ,
, ![]() , следовательно, условие неравенства (4) целей выполняется.
, следовательно, условие неравенства (4) целей выполняется.
![]() , (5)
, (5)
Так как ![]() , следовательно, весовым коэффициентам корректировки не требуется.
, следовательно, весовым коэффициентам корректировки не требуется.
Результаты исследования представлены в таблице 3.
Таблица 3.
Матрица нормированных критериев
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Производится нормировка показателей достижения целей и перестраивается таблица 2 на их нормированные значения, которые представлены в таблице 4.
Таблица 4.
Матрица нормированных критериев с учетом приоритета достижения целей
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По максимальной эффективности предложенные варианты можно ранжировать в порядке возрастания: I3, I2, I1, I5, I6, I4.
В качестве оптимального варианты (стратегии) принимается вариант, у которого оценка общей эффективности максимальна:
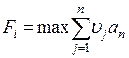 ,
,
где: υj — нормированные значения критериев.
Например,
 о.е.
о.е.
В том случае, если больший приоритет присваивается такому критерию как капитальные вложения, то весовые коэффициенты будут распределены следующим образом: а1=0.4, а2=0.5, а3=0.1.
Результаты данного исследования сведены в таблицу 5.
Производится нормировка показателей достижения целей и перестраивается таблица 2 на их нормированные значения, представленные в таблице 6.
По максимальной эффективности варианты 1÷6 можно ранжировать в порядке возрастания: I3, I5, I6, I2, I1, I4.
Таблица 5.
Матрица нормированных критериев
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 6.
Матрица нормированных критериев с учетом приоритета достижения целей
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В этом случае, оптимальным считается вариант 4 – I4 с максимальной оценкой эффективности:

Изложенный метод может использоваться при исследовании вариантов новых технических решений в условиях недостаточности информации.
Однако он имеет ряд недостатков:
1. возможность субъективных решений;
2. отсутствие нормативов соизмерения различных целей;
3. приравнивание в некоторых случаях затрат и результатов.
Чтобы избежать отмеченных недостатков, связанных с использованием экспертных методов, необходимо ввести экономические соображения в оценку различных целей.
Например, среди целей О1…On можно выделить главную цель — капитальные затраты. Далее, необходимо рассмотреть зависимость капитальных затрат от степени достижения прочих целей.
В результате выбор варианта можно производить по следующему выражению:
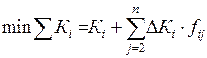 ,
,
где: Кi — непосредственно капитальные затраты по варианту;
ΔКi — прирост капитальных затрат на единицу изменения показателя степени достижения цели Oj.
Список литературы:
1.Машунин Ю.К. Информационные технологии моделирования технических систем на базе методов векторной оптимизации // Информационные технологии. — 2001. — № 9. — с. 14—21.
2.Машунин Ю.К., Торгашов А.Ю. Математические основы управления в экономике. Учебное пособие. Находка: Институт технологии и бизнеса, 2003. — 216 с.
дипломов


Оставить комментарий